File:B271t.png

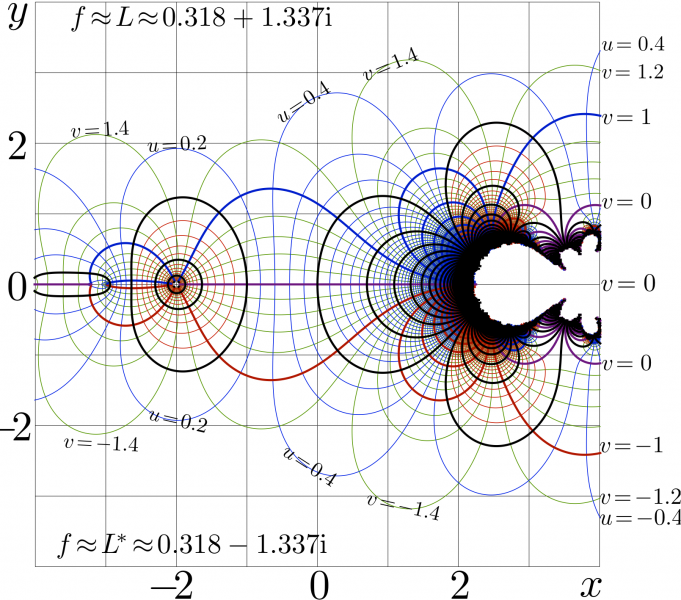
Complex map of tetration to base $\mathrm e$, isolines of real and imaginary parts of

$f\!=\!\mathrm{tet}(x + \mathrm i y)$ are shown in the $x$,$y$ plane,

range: $~-4\! \le\! x \le 4~$; $~-4\! \le\! y \le 4~$.

Levels $u\!=\!\Re(f)\!=\!\mathrm {const}$ and $v\!=\!\Im(f)\!=\!\mathrm {const}$ are plotted; integer values correspond to the thick lines.

C++ generator of curves

// Files conto.cin, ado.cin, fsexp.cin, plofu.cin should be loaded to the working directory for the compilation of the code below.

#include <math.h>
#include <stdio.h>
#include <stdlib.h>
#define DB double
#define DO(x,y) for(x=0;x<y;x++)
using namespace std;
#include<complex>
typedef complex<double> z_type;
#define Re(x) x.real()
#define Im(x) x.imag()
#define I z_type(0.,1.)
#include "conto.cin"
#include "fsexp.cin"
//#include "fslog.cin"
main(){ int j,k,m,n; DB x,y, p,q, t; z_type z,c,d, cu,cd;
int M=401,M1=M+1;
int N=401,N1=N+1;
DB X[M1],Y[N1], g[M1*N1],f[M1*N1], w[M1*N1]; // w is working array.
char v[M1*N1]; // v is working array
FILE *o;o=fopen("b271t0.eps","w");  ado(o,87,87);
fprintf(o,"46 45 translate\n 10 10 scale\n");
DO(m,M1) X[m]=-4.+.02*(m-.5);
DO(n,N1) Y[n]=-4.+.02*(n-.5);
for(m=-4;m<5;m++) {M(m,-4)L(m,4)}
for(n=-4;n<5;n++) {M(  -4,n)L(4,n)} fprintf(o,".006 W 0 0 0 RGB S\n");
fprintf(o,"/adobe-Roman findfont .6 scalefont setfont\n");
DO(m,M1)DO(n,N1){      g[m*N1+n]=9999;
                       f[m*N1+n]=9999;}
DB b=sqrt(2);
DO(m,M1){x=X[m]; printf("x=%6.3f\n",x);
DO(n,N1){y=Y[n]; z=z_type(x,y); if(abs(z+2.)>.04)
       { c=FSEXP(z);
//       c=FSLOG(z);
         p=Re(c); q=Im(c);
         if(p>-9999 && p<9999 && fabs(q)>1.e-12) g[m*N1+n]=p;
         if(q>-9999 && q<9999 && fabs(q)>1.e-12) f[m*N1+n]=q;
       }
        }}
fprintf(o,"1 setlinejoin 2 setlinecap\n");
p=2.; q=1.1;;
#include "plofu.cin"
fprintf(o,"0 setlinejoin 0 setlinecap\n");
fprintf(o,"showpage\n");
fprintf(o,"%cTrailer\n",'%');
fclose(o);
       system("epstopdf b271t0.eps"); 
       system(    "open b271t0.pdf"); //for macintosh
       getchar(); system("killall Preview"); // For macintosh

}

Latex generator of labels

\documentclass[12pt]{article} %<br> \paperheight 680px %<br> \paperwidth 772px %<br> \textwidth 1294px %<br> \textheight 1200px %<br> \topmargin -110px %<br> \oddsidemargin -80px %<br> \usepackage{graphics} %<br> \usepackage{rotating} %<br> \newcommand \sx {\scalebox} %<br> \newcommand \rot {\begin{rotate}} %<br> \newcommand \ero {\end{rotate}} %<br> \newcommand \ing {\includegraphics} %<br> \newcommand \rmi {\mathrm{i}} %<br> \begin{document} %<br> \newcommand \zoomax { %<br> \put(2, 82.6){\sx{.6}{$y$}} %<br> \put(2, 63.3){\sx{.5}{$2$}} %<br> \put(2, 43.3){\sx{.5}{$0$}} %<br> \put(-1, 23.3){\sx{.5}{$-\!2$}} %<br> \put(22, 0.8){\sx{.5}{$-\!2$}} %<br> \put(45, 0.8){\sx{.5}{$0$}} %<br> \put(65, 0.8){\sx{.5}{$2$}} %<br> \put(84,1){\sx{.5}{$x$}} %<br> } %<br> \parindent 0pt %<br> \sx{8}{\begin{picture}(86,86) \put(0,0){\ing{b271t0}} %<br> \zoomax %<br> \put(7,44){\sx{.4}{\bf cut}} %<br> \put(7,81){\sx{.4}{$f\approx L\approx0.318+1.337i$}} %<br> \put(6,6){\sx{.4}{$f\approx L^*\approx0.318-1.337i$}} %<br> \put(87,78){\sx{.31}{$u\!=\!0.4$}} %<br> \put(87,74){\sx{.31}{$v\!=\!1.2$}} %<br> \put(87,68){\sx{.32}{$v\!=\!1$}} %<br> \put(87,56){\sx{.32}{$v\!=\!0$}} %<br> \put(87,44){\sx{.32}{$v\!=\!0$}} %<br> \put(87,33){\sx{.31}{$v\!=\!0$}} %<br> \put(87,21){\sx{.31}{$v\!=\!-\!1$}} %<br> \put(86,14){\sx{.29}{$v\!=\!-\!1.2$}} %<br> \put(87, 11){\sx{.30}{$u\!=\!0.4$}} %<br> \put(10.2,66){\sx{.3}{\rot{2}$v\!=\!1.4$\ero}} \put(55.2,77){\sx{.3}{\rot{2}$v\!=\!1.4$\ero}} %<br> \put(10,22){\sx{.3}{\rot{-2}$v\!=\!-\!1.4$\ero}} \put(55,12){\sx{.3}{\rot{-2}$v\!=\!-\!1.4$\ero}} %<br> \put(22,64){\sx{.3}{\rot{15}$u\!=\!0.2$\ero}} \put(41,71){\sx{.3}{\rot{16}$u\!=\!0.4$\ero}} %<br> \put(22,25){\sx{.3}{\rot{-15}$u\!=\!0.2$\ero}} \put(41,18){\sx{.3}{\rot{-16}$u\!=\!0.4$\ero}} %<br> \end{picture}} %<br> \end{document}

References

http://www.ils.uec.ac.jp/~dima/PAPERS/2009analuxpRepri.pdf D.Kouznetsov. Analytic solution of F(z+1)=exp(F(z)) in complex z-plane. Mathematics of Computation, v.78 (2009), 1647-1670.

http://tori.ils.uec.ac.jp/PAPERS/2010vladie.pdf D.Kouznetsov. Superexponential as special function. Vladikavkaz Mathematical Journal, 2010, v.12, issue 2, p.31-45.

Copyleft 2009–2011 by Dmitrii Kouznetsov: Use for free, attribute the source. The generators are available and will be uploaded upon request.