File:ExpMap600.jpg
ExpMap600.jpg (600 × 593 pixels, file size: 101 KB, MIME type: image/jpeg)
Summary
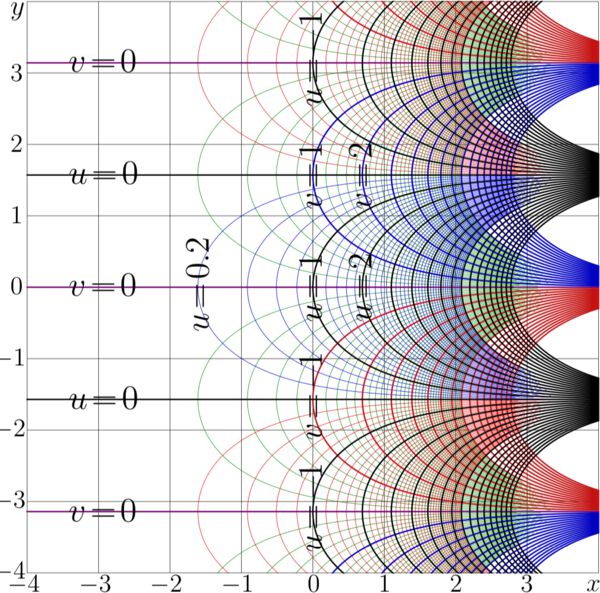
Complex map of exp: \[u+\mathrm iv=\exp(x\!+\!\mathrm iy)\]
This map appears as figure 14.2 at page 177 of book «Superfunctions»[1].
The map is included in the Book in order to compare it to maps of other related functions;
in particular, those of
Logarithm (inverse function of exponential) \(\ln=\exp^{-1}\)
tetration (SuperExponential) tet as solution of transfer equation
\(~ \mathrm{tet}(z\!+\!1)=\exp(\mathrm{tet}(z))\) ,
ArcTetration (AbelExponential) \( \mathrm{ate}=\mathrm{tet}^{-1} ~\) and
non-integer iterates of exponential,
\[
\exp^n(z)=\mathrm{tet}\big(n+\mathrm{ate}(z)\big)
\]
Number \(n\) of iterate in this expression has no need to be integer; it can be real or even a complex number.
C++ generator of map
/* Files ado.cin and conto.cin should be loaded in order to compile the code below.*/
#include <math.h>
#include <stdio.h>
#include <stdlib.h>
#define DB double
#define DO(x,y) for(x=0;x<y;x++)
using namespace std;
#include<complex>
typedef complex<double> z_type;
#define Re(x) x.real()
#define Im(x) x.imag()
#define I z_type(0.,1.)
#include "conto.cin"
//#include "fsexp.cin"
//#include "fslog.cin"
main(){ int j,k,m,n; DB x,y, p,q, t; z_type z,c,d, cu,cd;
int M=401,M1=M+1;
int N=401,N1=N+1;
DB X[M1],Y[N1];
DB *g, *f, *w; // w is working array.
g=(DB *)malloc((size_t)((M1*N1)*sizeof(DB)));
f=(DB *)malloc((size_t)((M1*N1)*sizeof(DB)));
w=(DB *)malloc((size_t)((M1*N1)*sizeof(DB)));
char v[M1*N1]; // v is working array
FILE *o;o=fopen("ExpMap.eps","w"); ado(o,802,802);
fprintf(o,"401 401 translate\n 100 100 scale\n");
fprintf(o,"1 setlinejoin 2 setlinecap\n");
DO(m,M1) X[m]=-4.+.02*(m-.5);
DO(n,N1) Y[n]=-4.+.02*(n-.5);
// for(n=0;n<N1;n++) Y[n]=sinh((2./200.)*(n-200.5));
for(m=-4;m<5;m++) {M(m,-4)L(m,4)}
for(n=-4;n<5;n++) {M( -4,n)L(4,n)} fprintf(o,".006 W 0 0 0 RGB S\n");
//fprintf(o,"/adobe-Roman findfont .6 scalefont setfont\n");
DO(m,M1)DO(n,N1){ g[m*N1+n]=999;
f[m*N1+n]=999;}
DB b=sqrt(2);
DO(m,M1){x=X[m]; printf("x=%6.3f\n",x);
DO(n,N1){y=Y[n]; z=z_type(x,y); //if(abs(z+2.)>.019)
{
c=exp(z);
// c=FSEXP(z);
// c=FSLOG(z);
p=Re(c); q=Im(c);
// if(p>-12 && p<12 && fabs(q)>1.e-12)
g[m*N1+n]=p;
// if(q>-12 && q<12 && fabs(q)>1.e-12)
f[m*N1+n]=q;
}
}}
fprintf(o,"1 setlinejoin 1 setlinecap\n");
p=2.;q=.3;
for(m=-8;m<8;m++)for(n=2;n<10;n+=2)conto(o,f,w,v,X,Y,M,N,(m+.1*n),-q,q);fprintf(o,".007 W 0 .6 0 RGB S\n");
for(m=0;m<8;m++) for(n=2;n<10;n+=2)conto(o,g,w,v,X,Y,M,N,-(m+.1*n),-q,q);fprintf(o,".007 W .9 0 0 RGB S\n");
for(m=0;m<8;m++) for(n=2;n<10;n+=2)conto(o,g,w,v,X,Y,M,N, (m+.1*n),-q,q);fprintf(o,".007 W 0 0 .9 RGB S\n");
for(m= 1;m<17;m++) conto(o,f,w,v,X,Y,M,N, (0.-m),-p,p);fprintf(o,".02 W .8 0 0 RGB S\n");
for(m= 1;m<17;m++) conto(o,f,w,v,X,Y,M,N, (0.+m),-p,p);fprintf(o,".02 W 0 0 .8 RGB S\n");
conto(o,f,w,v,X,Y,M,N, (0. ),-p,p); fprintf(o,".02 W .5 0 .5 RGB S\n");
for(m=-16;m<17;m++)conto(o,g,w,v,X,Y,M,N,(0.+m),-p,p);fprintf(o,".02 W 0 0 0 RGB S\n");
//
/*
M(-2,0)L(-4,0)fprintf(o,"0 setlinecap .03 W 1 1 1 RGB S\n");
for(n=0;n<11;n++){ M(-2-.2*(n+.2),0) L(-2-.2*(n+.45),0) } fprintf(o,".04 W 1 .5 0 RGB S\n");
for(n=0;n<21;n++){ M(-2-.2*(n+.7),0) L(-2-.2*(n+.95),0) } fprintf(o,".04 W 0 .5 1 RGB S\n");
*/
//#include "plofu.cin"
fprintf(o,"0 setlinejoin 0 setlinecap\n");
fprintf(o,"showpage\n");
fprintf(o,"%c%cTrailer\n",'%','%');
fclose(o);
free(f);
free(g);
free(w);
system("epstopdf ExpMap.eps");
system( "open ExpMap.pdf"); //for macintosh
// getchar(); system("killall Preview"); // For macintosh
}
References
https://en.wikipedia.org/wiki/Exponential_function In mathematics, the exponential function is the unique real function which maps zero to one and has a derivative everywhere equal to its value. The exponential of a variable \(x\) is denoted \(\exp x\) or \(e^x\), with the two notations used interchangeably. It is called exponential because its argument can be seen as an exponent to which a constant number e ≈ 2.718, the base, is raised. There are several other definitions of the exponential function, which are all equivalent although being of very different nature. ..
https://en.citizendium.org/wiki/Exponential_function The exponential function of \(z\), denoted by \( \exp(z)\) or \(e^z\), can be defined as the solution of the differential equation \[ \exp^{\prime}(z)\equiv \frac{d e^z}{dz}=\exp(z)\] with the additional condition \[ \exp(0)=1.\, \]
Keywords
«Complex map», «exp», «Superfunctions»,
File history
Click on a date/time to view the file as it appeared at that time.
| Date/Time | Thumbnail | Dimensions | User | Comment | |
|---|---|---|---|---|---|
| current | 10:53, 8 December 2025 |  | 600 × 593 (101 KB) | T (talk | contribs) | == Summary == {{oq|ExpMap600.jpg|}} Complex map of exp: \[u+\mathrm iv=\exp(x\!+\!\mathrm iy)\] This map appears as figure 14.2 at page 177 of book «Superfunctions»<ref name="b"> https://www.amazon.co.jp/-/en/Dmitrii-Kouznetsov/dp/6202672862 <br> https://www.morebooks.de/shop-ui/shop/product/978-620-2-67286-3 <br> https://mizugadro.mydns.jp/BOOK/468.pdf <br> D.Kouznetov. Superfunctions. Lambert Academic Publishing, 2020. </ref>. ==C++ generator of map== /* Files [... |
You cannot overwrite this file.
File usage
The following page uses this file: