BesselY0
BesselY0, called also Neumann function, and also $\mathrm{BesselY}_0$ or simply $Y_0$ is kind of Bessel function (or Cylindric function), solution $f=f(z)$ of the Bessel equation
- $ \!\!\!\!\!\!\!\!\!\! (1) ~ ~ ~ \displaystyle
f+f'/z+f=0$
with integral representation
- $\!\!\!\!\!\!\!\!\!\!\!\!\!\!
\displaystyle Y_0(x)=\frac{-2}{\pi} \int_0^\infty \cos(x \cosh(t)) \mathrm d t$
valid at least for $x>0$.
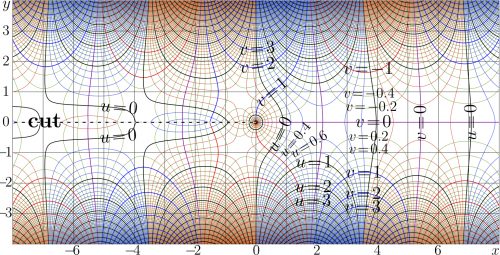
The explicit plot of $Y_0$ of real argument is shown at the upper right corner, for comparison, $J_0$ and $J_1$ are also plotted; the complex map of $Y_0$ is shown below.
Various notations
In the literture, and in particular, in the first editions of the tables by Granshtein,Ryzhik, BesselY0 is called Neumann function and denoted $N_0$. In the latest editions and in the tables by Abramowits,Stegun, notation $Y_0$ is used. In Mathematica, BesselY0(z) can be accessed with BesselY[0,z] and is interpreted as "Bessel function of Second kind" [1]
Relation to $J_0$
In the upper half–plane, id est, for $\Re(z)>0$, the following relation with BesselJ0 takes place:
- $Y_0(z)=Y_0(-z)+2~ \mathrm i~ J_0(-z)$
At $\Re(z)<0$, the similar relation is valid:
- $Y_0(z)=Y_0(-z)- 2~ \mathrm i~ J_0(-z)$
These formulas are used for evaluation of $Y_0(z)$ at $\Re(z)<0$ in the C++ complex(double) implementation Bessely0.cin .
Behavior at zero
- $ \!\!\!\!\!\!\!\!\!\! (2) ~ ~ ~ \displaystyle
Y_0(z)=\frac{2 (\log (z)+\gamma -\log (2))}{\pi
}+\frac{z^2 (-\log (z)-\gamma +1+\log (2))}{2
\pi }+\frac{z^4 (2 \log (z)+2 \gamma -3-2 \log
(2))}{64 \pi }+O\left(z^6\right)
$ where $~\gamma=$EulerGamma$~\approx 0.5772156649015329~$ is universal constant.
Expansion at large values of the argument
At large $|z|$, the expansion of $Y_0$ can be written in analogy with that for $J_0$:
- $ \!\!\!\!\!\!\!\!\!\!\!\! (3) ~ ~ ~ \displaystyle
J_0(z)=\sqrt{\frac{2}{\pi z}} \left( \left(\frac{1}{8 z} -\frac{75}{1024 z^3}+O\left(\frac{1}{z^5}\right)\right) \sin \left(z-\frac{\pi }{4}\right) +\left(1-\frac{9}{128 z^2}+\frac{3675}{32768 z^4}+O\left(\frac{1}{z^6}\right)\right) \cos \left(z-\frac{\pi }{4}\right) \right) $
- $ \!\!\!\!\!\!\!\!\!\!\!\! (4) ~ ~ ~ \displaystyle
Y_0(z)=\sqrt{\frac{2}{\pi z}} \left( \left(\frac{-1}{8 z}+\frac{75}{1024 z^3}+O\left(\frac{1}{z^5}\right)\right) \cos \left(z-\frac{\pi }{4}\right) +\left(1-\frac{9}{128 z^2}+\frac{3675}{32768 z^4}+O\left(\frac{1}{z^6}\right)\right) \sin \left(z-\frac{\pi }{4}\right) \right) $
Keywords
Bessel function BesselJ0 BesselJ1 BesselH0
References
- ↑ http://mathworld.wolfram.com/BesselFunctionoftheSecondKind.html Bessel Function of the Second Kind
