File:QexpMapT400.jpg

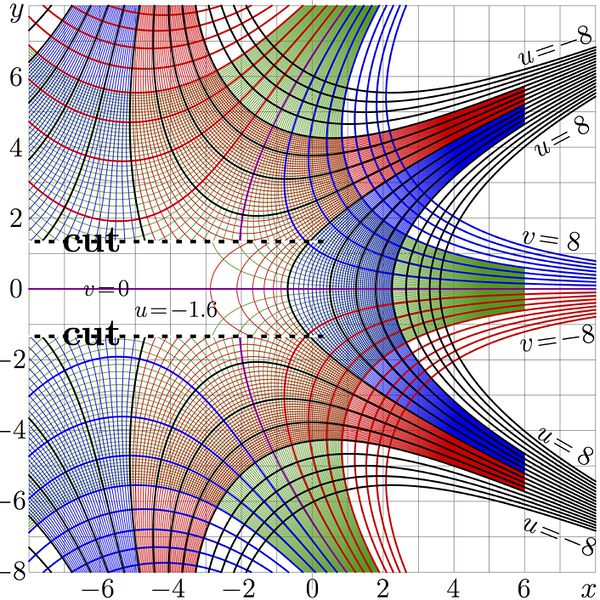
Complex map of function $\sqrt(\exp)= \exp^{1/2}$, Halfiteration of exponential to base $\mathrm e$.

$f=\exp^{1/2}(x+\rm i y$

is shown with lines $u=\Re(f)=\mathrm const$ and lines $v=\Im(f)=\mathrm const$.

C++ generator of curves

// FIles ado.cin and conto.cin and superexp.cin and superlo.cin should be loaded in the working directory in order to compile the code below. Actually, the last two evaluate tetration tet and arcterration ate; routines fsexp.cin and fslog.cin can be used instead.

#include <math.h> 
#include <stdio.h>
#include <stdlib.h>
#define DB double
#define DO(x,y) for(x=0;x<y;x++)
using namespace std;
#include <complex>
typedef complex<double> z_type;
#define Re(x) x.real()
#define Im(x) x.imag()
#define I z_type(0.,1.)
//#include "fac.cin"
//#include "sinc.cin"
//#include "facp.cin"
//#include "afacc.cin"
//#include "superfac.cin"
#include "superex.cin"
#include "superlo.cin"
DB xL=0.31813150520476413;
DB yL=1.3372357014306895;

#include "conto.cin"

int main(){ int j,k,m,n,n1; DB x,y, p,q, t; z_type z,c,d;
 int M=160,M1=M+1;
 int N=165,N1=N+1;
DB X[M1],Y[N1], g[M1*N1],f[M1*N1], w[M1*N1]; // w is working array.
char v[M1*N1]; // v is working array
//FILE *o;o=fopen("fig4b.eps","w");ado(o,402,402);
FILE *o;o=fopen("qexpMap.eps","w");ado(o,402,402);
fprintf(o,"201 201 translate\n 20 20 scale\n");
DO(m,M1) X[m]=-8.+.1*m;
DO(n,N1){   y=-8.+.1*n; if(y< -yL) Y[n]=y; else break;}
        Y[n]=-yL-.001; n++;
        Y[n]=-yL+.001; n++;
for(j=n;j<N1;j++){y=-8.+.1*(j-2); if(y<-.02) Y[j]=y; else break;}
        Y[j]= -.02; j++;
        Y[j]= +.02; j++;
for(k=j;k<N1;k++){y=-8.+.1*(k-3); if(y<yL) Y[k]=y; else break;}
        Y[k]= yL-.001; k++;
        Y[k]= yL+.001; k++;
for(n=k;n<N1;n++){y=-8.+.1*(n-5); Y[n]=y;}
for(m=-8;m<9;m++){if(m==0){M(m,-8.5)L(m,8.5)} else{M(m,-8)L(m,8)}}
for(n=-8;n<9;n++){      M(  -8,n)L(8,n)}
fprintf(o,".008 W 0 0 0 RGB S\n");
DO(m,M1)DO(n,N1){g[m*N1+n]=9999; f[m*N1+n]=9999;}
DO(m,M1){x=X[m]; //printf("%5.2f\n",x);
DO(n,N1){y=Y[n]; z=z_type(x,y); 
//      c=afacc(z);
//      c=fac(c);
//      c=arcsuperfac(z);
//      c=superfac(.5+c);
        c=FSLOG(z);
        c=FSEXP(.5+c);
//      d=z;
//      p=abs(c-d)/(abs(c)+abs(d));  p=-log(p)/log(10.)-1.;
        p=Re(c);q=Im(c);        
        if(p>-999 && p<999)     g[m*N1+n]=p;
        if(q>-999 && q<999 && fabs(q)> 1.e-14) f[m*N1+n]=q;
                        }}
fprintf(o,"1 setlinejoin 1 setlinecap\n"); p=6.;q=6.;
//#include"plofu.cin"
//p=2;q=1;
for(m=-4;m<4;m++) for(n=1;n<10;n+=1)conto(o,f,w,v,X,Y,M-20,N,(m+.1*n),-q, q); fprintf(o,".02 W 0 .6 0 RGB S\n");
for(m= 0;m<4;m++) for(n=1;n<10;n+=1)conto(o,g,w,v,X,Y,M-20,N,-(m+.1*n),-q, q); fprintf(o,".02 W .9 0 0 RGB S\n");
for(m= 0;m<4;m++) for(n=1;n<10;n+=1)conto(o,g,w,v,X,Y,M-20,N, (m+.1*n),-q, q); fprintf(o,".02 W 0 0 .9 RGB S\n");
for(m=1;m<9;m++)  conto(o,f,w,v,X,Y,M,N, (0.-m),-p,p); fprintf(o,".05 W .9 0 0 RGB S\n");
for(m=1;m<9;m++)  conto(o,f,w,v,X,Y,M,N, (0.+m),-p,p); fprintf(o,".05 W 0 0 .9 RGB S\n");
                  conto(o,f,w,v,X,Y,M,N, (0.  ),-p,p); fprintf(o,".05 W .6 0 .6 RGB S\n");
for(m=-8;m<9;m++) conto(o,g,w,v,X,Y,M,N, (0.+m),-p,p); fprintf(o,".05 W 0 0 0 RGB S\n");
fprintf(o,"0 setlinejoin 0 setlinecap\n");
M(xL, yL)L(-8.1, yL) 
M(xL,-yL)L(-8.1,-yL) fprintf(o,"                  .06 W 1 1 1 RGB S\n");
DO(m,21){M(xL-.4*m, yL)L(xL-.4*(m+.4), yL)}
DO(m,21){M(xL-.4*m,-yL)L(xL-.4*(m+.4),-yL)} fprintf(o,".1 W 0 0 0 RGB S\n");
//M(xL, yL)L(-8, yL)
//M(xL,-yL)L(-8,-yL) fprintf(o,"[.2 .2]0 setdash .12 W 0 0 0 RGB S\n");
fprintf(o,"showpage\n%c%cTrailer",'%','%'); fclose(o);
//      system(    "open fig4b.eps");           //for macintosh
       system("epstopdf qexpMap.eps");
       system(    "open qexpMap.pdf");         //for  unix
//      system(    "xpdf fig4b.pdf &");         //for  unix
//      getchar(); system("killall Preview");   //for macintosh
}

Latex generator of labels

References

Categrory:Tetration