File:Exm09mapT200.jpg
Original file (2,281 × 1,179 pixels, file size: 560 KB, MIME type: image/jpeg)
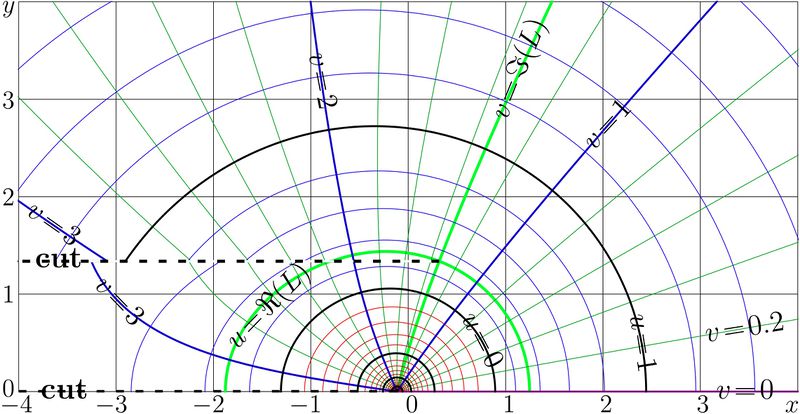
Complex map of the $-0.9$th iteration of exponent, which is also $0.9$th iteration of logarithm;
$u+\mathrm i v= \exp^{-0.9}(x+\mathrm i y)=\ln^{0.9}(x+\mathrm i y)= \mathrm{tet}(-0.9+\mathrm{ate}(x+\mathrm i y))$
For the evaluation, the non-integer iterate of exponential is expressed through tetration tet and arctetration ate. The complex double implementations FSEXP and FSLOG are used in the C++ code below.
C++ generator of curves
// Files ado.cin, conto.cin, fsexp.cin and fslog.cin should be loaded in the working directory in order to compile the code below.
#include <math.h>
#include <stdio.h>
#include <stdlib.h>
#define DB double
#define DO(x,y) for(x=0;x<y;x++)
using namespace std;
#include<complex>
typedef complex<double> z_type;
#define Re(x) x.real()
#define Im(x) x.imag()
#define I z_type(0.,1.)
#include "conto.cin"
#include "fsexp.cin"
#include "fslog.cin"
main(){ int j,k,m,n; DB x,y, p,q, t; z_type z,c,d, cu,cd;
int M=401,M1=M+1;
int N=403,N1=N+1;
DB X[M1],Y[N1];
DB *g, *f, *w; // w is working array.
g=(DB *)malloc((size_t)((M1*N1)*sizeof(DB)));
f=(DB *)malloc((size_t)((M1*N1)*sizeof(DB)));
w=(DB *)malloc((size_t)((M1*N1)*sizeof(DB)));
char v[M1*N1]; // v is working array
FILE *o;o=fopen("exm09map.eps","w"); ado(o,802,402);
fprintf(o,"401 1 translate\n 100 100 scale\n");
fprintf(o,"1 setlinejoin 2 setlinecap\n");
DO(m,M1) X[m]=-4+.02*(m-.5);
DO(n,N1) { y=0.+.01*(n-.5); if(y>Im(Zo)) break; Y[n]=y; }
Y[n] =Im(Zo)-.00001;
Y[n+1]=Im(Zo)+.00001;
for(m=n+2;m<N1;m++) Y[m]=.01*(m-2-.5);
for(m=-4;m<5;m++){M(m,0) L(m,4) }
for(n=0;n<5;n++){M( -4,n) L(4,n)}
fprintf(o,".006 W 0 0 0 RGB S\n");
DO(m,M1)DO(n,N1){ g[m*N1+n]=999; f[m*N1+n]=999;}
DO(m,M1){x=X[m]; if(m/10*10==m) printf("x=%6.3f\n",x);
DO(n,N1){y=Y[n]; z=z_type(x,y); //if(abs(z+2.)>.019)
c=FSEXP(-.9+FSLOG(z));
p=Re(c); q=Im(c);// if(p>-19 && p<19 && ( x<2. || fabs(q)>1.e-12 && fabs(p)>1.e-12) )
{ g[m*N1+n]=p;f[m*N1+n]=q;}
}}
fprintf(o,"1 setlinejoin 1 setlinecap\n"); p=2.;q=1;
conto(o,g,w,v,X,Y,M,N, Re(Zo),-p,p);fprintf(o,".03 W 0 1 0 RGB S\n");
conto(o,f,w,v,X,Y,M,N, Im(Zo),-p,p);fprintf(o,".03 W 0 1 0 RGB S\n");
for(m=-8;m<8;m++)for(n=2;n<10;n+=2)conto(o,f,w,v,X,Y,M,N,(m+.1*n),-q,q);fprintf(o,".007 W 0 .6 0 RGB S\n");
for(m=0;m<8;m++) for(n=2;n<10;n+=2)conto(o,g,w,v,X,Y,M,N,-(m+.1*n),-q,q);fprintf(o,".007 W .9 0 0 RGB S\n");
for(m=0;m<8;m++) for(n=2;n<10;n+=2)conto(o,g,w,v,X,Y,M,N, (m+.1*n),-q,q);fprintf(o,".007 W 0 0 .9 RGB S\n");
for(m= 1;m<17;m++) conto(o,f,w,v,X,Y,M,N, (0.-m),-q,q);fprintf(o,".02 W .8 0 0 RGB S\n");
for(m= 1;m<17;m++) conto(o,f,w,v,X,Y,M,N, (0.+m),-q,q);fprintf(o,".02 W 0 0 .8 RGB S\n");
conto(o,f,w,v,X,Y,M,N, (0. ),-p,p); fprintf(o,".02 W .5 0 .5 RGB S\n");
for(m=-16;m<17;m++)conto(o,g,w,v,X,Y,M,N,(0.+m),-q,q);fprintf(o,".02 W 0 0 0 RGB S\n");
fprintf(o,"0 setlinejoin 0 setlinecap\n");
M(Re(Zo),Im(Zo))L(-4,Im(Zo)) fprintf(o,"1 1 1 RGB .022 W S\n");
DO(n,40){M(Re(Zo)-.2*n,Im(Zo))L(Re(Zo)-.2*(n+.4),Im(Zo)) }
fprintf(o,"0 0 0 RGB .032 W S\n");
DO(n,20){M(-4+.2*n,0) L(-4+.2*(n+.4),0) }
fprintf(o,"0 0 0 RGB .032 W S\n");
fprintf(o,"showpage\n");
fprintf(o,"%c%cTrailer\n",'%','%');
fclose(o); free(f); free(g); free(w);
system("epstopdf exm09map.eps");
system( "open exm09map.pdf"); //for macintosh
getchar(); system("killall Preview"); // For macintosh
}
Latex generator of labels
%
\documentclass[12pt]{article}
%
File history
Click on a date/time to view the file as it appeared at that time.
| Date/Time | Thumbnail | Dimensions | User | Comment | |
|---|---|---|---|---|---|
| current | 12:55, 28 July 2013 |  | 2,281 × 1,179 (560 KB) | T (talk | contribs) | resolution |
| 12:16, 28 July 2013 |  | 1,711 × 885 (382 KB) | T (talk | contribs) | shift | |
| 10:51, 28 July 2013 |  | 2,281 × 1,179 (560 KB) | T (talk | contribs) | Complex map of the $-0.9$th iteration of exponent, which is also $0.9$th iteration of logarithm; $u+\mathrm i v= \exp^{-0.9}(x+\mathrm i y)=\ln^{0.9}(x+\mathrm i y)= \mathrm{tet}(-0.9+\mathrm{ate}(x+\mathrm i y))$ For the evaluation, the non... |
You cannot overwrite this file.
File usage
The following page uses this file: