File:Fracit10t150.jpg
Revision as of 21:18, 4 August 2013 by T (talk | contribs) (Iterate of linear fraction; $\displaystyle f(z)=\frac{x}{c+z}$ at $c\!=\!2$. In general the $n$th iterate of $f$ can be expressed as follows: $\displaystyle f^n(z)=\frac{z}{c^n+\frac{1-c^n}{1-c} z}$ $y=f^n(x)$ is plotted versus $x$ for various...)
Size of this preview: 600 × 600 pixels. Other resolutions: 240 × 240 pixels | 1,466 × 1,466 pixels.
Original file (1,466 × 1,466 pixels, file size: 564 KB, MIME type: image/jpeg)
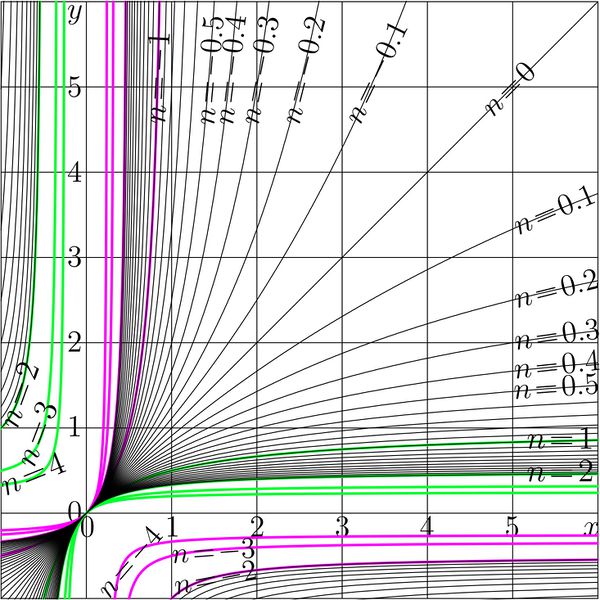
$\displaystyle f(z)=\frac{x}{c+z}$ at $c\!=\!2$.
In general the $n$th iterate of $f$ can be expressed as follows:
$\displaystyle f^n(z)=\frac{z}{c^n+\frac{1-c^n}{1-c} z}$
$y=f^n(x)$ is plotted versus $x$ for various values of $n$.
Generator of curves
// File ado.cin should be loaded to the working directory in order to compile the C++ code below.
//
#inc
//
Latex generator of labels
%File Fracit20t.pdf should be generated with the code above in order to compile the Latex document below.
%
\do
%
References
File history
Click on a date/time to view the file as it appeared at that time.
| Date/Time | Thumbnail | Dimensions | User | Comment | |
|---|---|---|---|---|---|
| current | 21:18, 4 August 2013 |  | 1,466 × 1,466 (564 KB) | T (talk | contribs) | Iterate of linear fraction; $\displaystyle f(z)=\frac{x}{c+z}$ at $c\!=\!2$. In general the $n$th iterate of $f$ can be expressed as follows: $\displaystyle f^n(z)=\frac{z}{c^n+\frac{1-c^n}{1-c} z}$ $y=f^n(x)$ is plotted versus $x$ for various... |
You cannot overwrite this file.
File usage
The following page uses this file: