Arcfactorial
ArcFactorial is the principal branch of the inverse function of Factorial;
- \( \mathrm{Factorial}(\mathrm{ArcFactorial}(z))=z\)
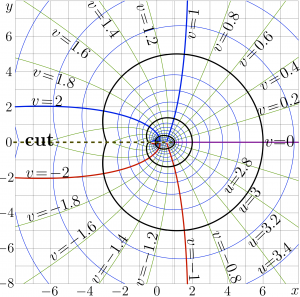
Complex map of \(f=\mathrm{ArcFactorial}(x\!+\!\mathrm i y)\) is shown at right in the \(x\), \(y\) plane with levels \(u=\Re(f)=\mathrm {const}\) and levels levels \(v=\Im(f)=\mathrm {const}\).
Contents
Notations
Also the notations
- \(\mathrm{afac}=\mathrm{ArcFactorial}=\mathrm{Factorial}^{-1}\)
are suggested.
However, \(\mathrm{Factorial}^{-1}(z)\) should not be confused with
- \(\displaystyle \mathrm{Factorial}(z)^{-1} = \frac{1}{\mathrm{Factorial}(z)}\)
and, in general, the \(c\)th iteration of Factorial, id est,
- \(\mathrm{Factorial}^x(z)\)
should not be confused with the \(c\)th power of \(z!\), which is
- \(\mathrm{Factorial}(z)^c\)
Properties of ArcFactorial
Attempting to give unique names to the real numbers, related to extrema and singularities of Factorial and ArcFactorial, these names are chosen from the personages of the serial The Sympsons. Suggestions about more suitable names should be appreciated.
ArcFactorial is holomorphic at the whole complex \(z\) plane except the half-line
- \(z\le \mathrm{Homer}\)
where
- \(\mathrm{Homer}=\mathrm{Factorial}(\mathrm{Bart})\approx 0.8856031944108887\)
and \(\mathrm{Bart}\approx 0.4616321449683622\) is solution of equation
- \(\mathrm{Factorial}'(\mathrm{Bart})=0\)
Bart is the branchpoint;
- \(\mathrm{ArcFactorial}(\mathrm{Homer})=\mathrm{Bart}\)
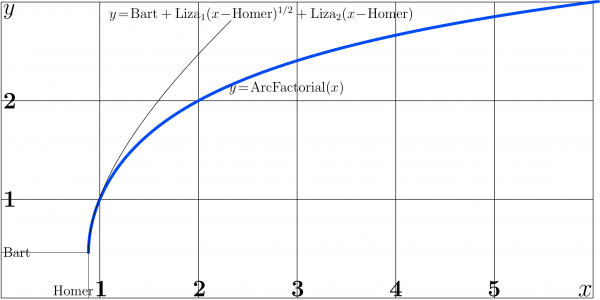
At large values of argument, the ArcFactorial shows slow growth, similar to that of logarithm.
Real argument and special cases
Behavior of ArcFactorial along the real axis is shown in figure at right.
For some natural values of argument, ArcFactorial has natural values:
- \(\mathrm{ArcFactorial}(1)=1\)
- \(\mathrm{ArcFactorial}(2)=2\)
- \(\mathrm{ArcFactorial}(6)=3\)
- \(\mathrm{ArcFactorial}(24)\!=4\)
and so on.
At certain specific values of argument, ArcFactorial has half-integer values:
- \(\displaystyle \mathrm{ArcFactorial}\left( \frac{\sqrt{\pi}}{2}\right)\!=\frac{1}{2}\)
- \(\displaystyle \mathrm{ArcFactorial}\left( \frac{3\sqrt{\pi}}{4}\right)\!=\frac{3}{2}\)
- \(\displaystyle \mathrm{ArcFactorial}\left( \frac{15\sqrt{\pi}}{8}\right)\!=\frac{5}{2}\)
Expansion at Homer
The expansion of Factorial at its minimum has form
- \(\mathrm{Factorial}(\mathrm{Bart}+t)=\mathrm{Homer} +\frac{1}{2}\mathrm{Factorial''}(\mathrm{Bart}) t^2 +\frac{1}{6}\mathrm{Factorial'''}(\mathrm{Bart}) t^3+ .. \)
The InverseSeries gives the expansion for the ArcFactorial:
- \(\mathrm{ArcFactorial}(\mathrm{Homer}+t)=\mathrm{Bart} + \mathrm{Liza}_1 t^{1/2} + \mathrm{Liza}_2 t + \mathrm{Liza}_3 t^{3/2}+ ...\)
where
- \(\mathrm{Liza}_1 =\sqrt{\frac{2}{\mathrm{Factorial}''(\mathrm{Bart})}} \approx ~ 1.5276760433847776\)
- \(\mathrm{Liza}_2 \approx ~ 0.3559463008501492\)
- \(\mathrm{Liza}_3 \approx \! -0.4620189870305121\)
- \(\mathrm{Liza}_4 \approx \! -0.19468729558612438 \)
References