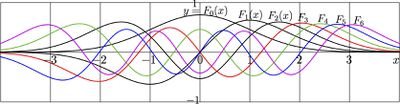
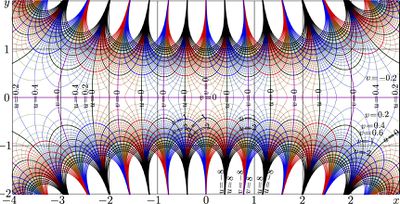
Oscillator function
Oscillator function, or, more correctly, the Harmonic oscillator wave function refers to the normalised solution $F_n$ of the stationary Schroedinger equation for the idealised dimension-less Harmonic Oscillator,
$F(x)+(2n\!+\!1-x^2)\, F(x) = 0$
For integer non-negative $n$, the solution $F_n$ can be expressed in terms of elementary functions,
$F_n(x)=h_n(x) \, \exp(-x^2/2)$ $=N_n^{-1/2}\, H_n(x)\, \exp(-x^2/2)$
through the Hermite polynomial
$H_n(x)=\mathrm{HermiteH}[n,x]$
and the Gaussian exponential; the scale of the exponential and the normalising factor
$N_n=2^n n! \sqrt{\pi}$
is chosen in such a way that
$\displaystyle \int_{-\infty}^{\infty} F_n(x)\, F_m(x)\, \mathrm d x= \delta_{m,n}$
Explicit plot $y\!=\!F_n(x)$ is shown in figure at top for $n=0 $..$6$. Below, the complex map of $F_6$ is shown with lines of constant real part and content imaginary part of $u\!+\!\mathrm i v=F_6(x\!+\!\mathrm i y)$.
At moderate values of the argument, the high oscillator function $F_n$ show almost sinusoidal (cosinusoidal) oscillations. Amplitude and period of these oscillations slowly decrease at the increase of the number $n$.
Hermite number
Value of the oscillator function at zero is determined by the Hermite number. It can be considered as function of number $n$ of the oscillator function.
There is special name for
$H_n=H_n(0)=\mathrm{HermiteH}[n,0]$.
It is called Hermite number; originally, $H_n$ is defined only for integer $n$. [1]
$\displaystyle H_n= \frac {2^n \sqrt{\pi}} {\displaystyle \mathrm{Factorial}\left(- \frac{1\!+\!n}{2}\right)}$ $\displaystyle = \left\{ \begin{array}{ccc} 0 & \mathrm{for ~ odd} & n \\ \displaystyle (-1)^{n/2} \frac{n!}{(n/2)!} &\mathrm{for ~ even} & n \end{array} \right.$
Then, the amplitude of oscillation of the oscillator function in vicinity of zero, at least for even $n$, can be expressed through the Hermite number as follows
$\displaystyle A_n=|F_n(0)|= \frac{|H_n|}{\sqrt{N_n}} $ $= \displaystyle \frac{\frac{n!}{(n/2)!}}{\sqrt{2^n n! \sqrt{\pi}}} $ $= \displaystyle \frac{\sqrt{n! / \sqrt{\pi}}} {2^{n/2} (n/2)! } $
For large values of argument, amplitude of the Oscillator function at zero has the following asymptote:
$A_n=\,$amos$(n)\approx \frac{(2/n)^{1/4}}{\sqrt{\pi}} $ $ \left( 1-\frac{1}{8n}+\frac{1}{128 n^2}+\frac{21}{1024 n^3}-\frac{85}{32768 n^4} -\frac{6511}{262144 n^5}+\frac{13989}{4194304n^6}+\frac{2539085}{33554432 n^7} -\frac{21469709}{2147483648 n^8} -\frac{7385563163 }{17179869184 n^9} +\frac{15306326687 }{274877906944 n^{10}} +O\left(\frac{1}{n^{11}}\right) \right) $
Approximation
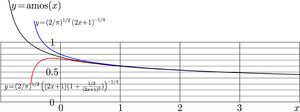
The oscillator function $F_n$, at n>1, oscillates along the real axis; and the number of zeros is exactly $n$. These oscillations can be revealed with the approximation, $\tilde F_n$ shown in figure at right for $n=$ $0..6$ in comparison to the oscillator functions $F$.
The approximations are constructed, assuming certain oscillation rate, that is determined by the energy of the state and the potential. It uses the analogy with the Born-Zommerfeld approximation. The approximation uses the following functions:
amos$(n)=H_n/\sqrt{N_n} =$ $\displaystyle \frac{2^{-n/2}\, \sqrt{n!}} {\pi^{1/4}\, (n/2)!}$
that determines amplitude of the oscillations of oscillator function number $n$, and
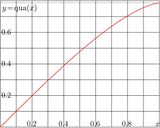
qua$(x)=\int_0^x \sqrt{1-z^2}\,\mathrm d z= $ $ \frac{1}{2}\big( x\,\sqrt{1\!-\!x^2}+\arcsin(x)\big)$
that determines the phase of the oscillations.
With functions amos and qua, the approximation of the oscillator function $F_n$ can be expressed as follows:
$\tilde F_n(x)=\,$ $\displaystyle \frac{\mathrm{amos}(n)}{\left(1-\frac{x^2}{2n+1}\right)^{1/4} }\,$ $\displaystyle \cos\left(\left(2n\!+\!1+\frac{1/4}{2n\!+\!1}\right)\, \mathrm{qua}\!\left(\frac{x}{\sqrt{2n\!+\!1}} \right) -\frac{\pi n}{2} \right)$
The approximation is valid only for $|x|<2n\!+\!1$; at the point, where the oscillator potential reaches value of the energy of the state, the approximation goes to infinity. In the central part, all the zeros of the oscillator function are reproduced well, $n\!-\!1$ oscillations are seen in the approximation; there, it returns of order of 2 correct decimal digits of the oscillator function.
References
- ↑ http://mathworld.wolfram.com/HermiteNumber.html Weisstein, Eric W. "Hermite Number." From MathWorld--A Wolfram Web Resource.
http://mathworld.wolfram.com/HermitePolynomial.html Weisstein, Eric W. "Hermite Polynomial." From MathWorld--A Wolfram Web Resource. (2016)