Difference between revisions of "File:AciplotTa.png"
(Importing image file) |
|||
| Line 1: | Line 1: | ||
| + | '''Plot of [[ArcCip]] of real argment'''. |
||
| − | Importing image file |
||
| + | |||
| + | $y=\mathrm{ArcCip}(x)$ in the $x$, $y$ plane. |
||
| + | |||
| + | ==Acip.cin== |
||
| + | This is preliminary version of the [[acip.cin]] file. It looks ugly, but it works! |
||
| + | |||
| + | z_type Cip(z_type z) {return cos(z)/z;} |
||
| + | z_type Cipp(z_type z) {return (-sin(z) - cos(z)/z)/z ;} |
||
| + | z_type ACip0(z_type z) {z_type t=1./(z*z); |
||
| + | return (1. |
||
| + | +t*(-1./2. |
||
| + | +t*(13./24. |
||
| + | +t*(-541./720. |
||
| + | +t*(9509./8064. |
||
| + | +t*(-7231801./3628800. |
||
| + | +t*(1695106117./479001600. |
||
| + | +t*(-567547087381./87178291200.))))))) |
||
| + | )/z ; } |
||
| + | |||
| + | z_type ACip1(z_type z){int n; z_type c=ACip0(z); |
||
| + | c+=.1*(z-Cip(c))/Cipp(c) ; |
||
| + | c+=.2*(z-Cip(c))/Cipp(c) ; |
||
| + | c+=.3*(z-Cip(c))/Cipp(c) ; |
||
| + | c+=.4*(z-Cip(c))/Cipp(c) ; |
||
| + | c+=.5*(z-Cip(c))/Cipp(c) ; |
||
| + | c+=.7*(z-Cip(c))/Cipp(c) ; |
||
| + | DO(n,8) c+=(z-Cip(c))/Cipp(c) ; |
||
| + | return c; |
||
| + | } // ACip0 does not know about the singulatiry. |
||
| + | |||
| + | z_type acos(z_type z){ |
||
| + | if(Im(z)<0){if(Re(z)>=0){return -I*log( z + sqrt(z*z-1.) );} |
||
| + | else{return -I*log( z - sqrt(z*z-1.) );}} |
||
| + | if(Re(z)>=0){return I*log( z + sqrt(z*z-1.) );} |
||
| + | else {return I*log( z - sqrt(z*z-1.) );} } |
||
| + | |||
| + | z_type ACipb(z_type z){ z_type t = 0.33650841691839534 + z ; z_type u=sqrt(t); |
||
| + | return |
||
| + | 2.798386045783887 |
||
| + | +u*(-2.437906425896532 |
||
| + | +u*(0.7079542331649882 |
||
| + | +u*(-.5009330133042798 |
||
| + | +u*(0.5714459932734446 |
||
| + | )))); } |
||
| + | |||
| + | z_type ACip3(z_type z){int n; z_type c=ACipb(z); |
||
| + | c+=.2*(z-Cip(c))/Cipp(c) ; |
||
| + | c+=.5*(z-Cip(c))/Cipp(c) ; |
||
| + | DO(n,8) c+=(z-Cip(c))/Cipp(c) ; |
||
| + | // DO(n,8) c=acos(c*z) ; |
||
| + | // DO(n,8) c=cos(c)/z ; |
||
| + | return c; |
||
| + | } |
||
| + | |||
| + | z_type ACip4(z_type z){int n; z_type z1=z_type(0,1.62134794610324); |
||
| + | z_type t=z-z1; |
||
| + | z_type c; |
||
| + | c=-z1+2.*sqrt(I*t); |
||
| + | // c=z1+t*(-2.+t*z_type(0,4.) ); |
||
| + | c+=.2*(z-Cip(c))/Cipp(c) ; |
||
| + | c+=.5*(z-Cip(c))/Cipp(c) ; |
||
| + | DO(n,8) c+=.9*(z-Cip(c))/Cipp(c) ; |
||
| + | return c; |
||
| + | } |
||
| + | |||
| + | z_type ACip5(z_type z){int n; |
||
| + | if(Re(z)>0 && abs(z)>1.2) return ACip1(z); |
||
| + | if(Re(z)>-2 && fabs(Im(z))<1.) return ACip3(z); |
||
| + | if(Im(z)>0) return ACip4(z); |
||
| + | return conj(ACip4(conj(z))); |
||
| + | } |
||
| + | |||
| + | |||
| + | |||
| + | ==C++ generator of curve== |
||
| + | |||
| + | Fiels [[ado.cin]] and [[acip.cin]] should be loaded at the working directory for compilation of the code below: |
||
| + | |||
| + | #include <math.h> |
||
| + | #include <stdio.h> |
||
| + | #include <stdlib.h> |
||
| + | #define DB double |
||
| + | #define DO(x,y) for(x=0;x<y;x++) |
||
| + | using namespace std; |
||
| + | #include <complex> |
||
| + | typedef complex<double> z_type; |
||
| + | #define Re(x) x.real() |
||
| + | #define Im(x) x.imag() |
||
| + | #define I z_type(0.,1.) |
||
| + | #include "ado.cin" |
||
| + | #include "acip.cin" |
||
| + | #define M(x,y) fprintf(o,"%6.4f %6.4f M\n",0.+x,0.+y); |
||
| + | #define L(x,y) fprintf(o,"%6.4f %6.4f L\n",0.+x,0.+y); |
||
| + | #define S(x,y) fprintf(o,"S\n",); |
||
| + | main(){ int j,k,m,n; DB x,y, p,q, t; z_type z,c,d; |
||
| + | DB y1= 1.1996786402577337; |
||
| + | DB zL= 2.798386045783887; |
||
| + | DB fL= -0.33650841691839534; |
||
| + | FILE *o;o=fopen("aciplot.eps","w");ado(o,320,330); |
||
| + | fprintf(o,"60 10 translate\n 100 100 scale\n"); |
||
| + | for(m=0;m<4;m++){M(m,0)L(m,3)} |
||
| + | for(n=0;n<4;n++){M(-.5,n)L(2.5,n)} |
||
| + | fprintf(o,"2 setlinecap .01 W 0 0 0 RGB S\n"); |
||
| + | for(m=-1;m<3;m++){M(.5+m,0)L(.5+m,3)} |
||
| + | for(n=0;n<4;n++){M(-.5,n+.5)L(2.5,n+.5)} |
||
| + | fprintf(o,"2 setlinecap .005 W 0 0 0 RGB S\n"); |
||
| + | M(fL,zL) |
||
| + | DO(m,2901){ x=-.336+.001*m; z=x; y=Re(ACip5(z)); L(x,y) } |
||
| + | fprintf(o,"1 setlinejoin 1 setlinecap .02 W .7 0 0 RGB S\n"); p=1.8;q=.7; |
||
| + | M(fL,0)L(fL,zL)L(0,zL) |
||
| + | fprintf(o,"2 setlinecap .003 W 0 0 0 RGB S\n"); |
||
| + | fprintf(o,"showpage\n%c%cTrailer",'%','%'); fclose(o); |
||
| + | system("epstopdf aciplot.eps"); |
||
| + | system( "open aciplot.pdf"); |
||
| + | getchar(); system("killall Preview");//for mac |
||
| + | } |
||
| + | |||
| + | ==Lated generator of lables== |
||
| + | |||
| + | File [[aciplot.pdf]] ahould be generated with the code above before to compile the [[Latex]] document below. |
||
| + | |||
| + | <nowiki> |
||
| + | % Copyleft 2012 by Dmitrii Kouznetsov %<br> |
||
| + | \documentclass[12pt]{article} %<br> |
||
| + | \usepackage{geometry} %<br> |
||
| + | \usepackage{graphicx} %<br> |
||
| + | \usepackage{rotating} %<br> |
||
| + | \paperwidth 610pt %<br> |
||
| + | \paperheight 610pt %<br> |
||
| + | \topmargin -92pt %<br> |
||
| + | \oddsidemargin -106pt %<br> |
||
| + | \textwidth 900pt %<br> |
||
| + | \textheight 900pt %<br> |
||
| + | \pagestyle {empty} %<br> |
||
| + | \newcommand \sx {\scalebox} %<br> |
||
| + | \newcommand \rot {\begin{rotate}} %<br> |
||
| + | \newcommand \ero {\end{rotate}} %<br> |
||
| + | \newcommand \ing {\includegraphics} %<br> |
||
| + | \begin{document} %<br> |
||
| + | \parindent 0pt \sx{2}{ \begin{picture}(340,310) %<br> |
||
| + | %\put(4,6){\ing{acosplot}} %<br> |
||
| + | \put(4,6){\ing{aciplot}} %<br> |
||
| + | \put(66,306){\sx{2}{$y$}} %<br> |
||
| + | \put(42,290){\sx{2}{$f_0$}} %v |
||
| + | \put(66,210){\sx{2}{\bf 2}} %<br> |
||
| + | \put(66,110){\sx{2}{\bf 1}} %<br> |
||
| + | \put(21, 21){\sx{2.1}{$z_0$}} %<br> |
||
| + | \put(58, 19){\sx{2}{\bf 0}} %<br> |
||
| + | \put(158, 19){\sx{2}{\bf 1}} %<br> |
||
| + | \put(258, 19){\sx{2}{\bf 2}} %<br> |
||
| + | \put(300, 21){\sx{2.1}{$x$}} %<br> |
||
| + | \put(168,94){\sx{1.6}{\rot{-16}$y\!=\!\mathrm{ACip}(x)$\ero}} \end{picture} %<br> |
||
| + | } %<br> |
||
| + | \end{document} |
||
| + | |||
| + | |||
| + | </nowiki> |
||
| + | |||
| + | |||
| + | [[Category:Explicit plot]] |
||
| + | [[Category:ArcCip]] |
||
Latest revision as of 09:41, 21 June 2013
Plot of ArcCip of real argment.
$y=\mathrm{ArcCip}(x)$ in the $x$, $y$ plane.
Acip.cin
This is preliminary version of the acip.cin file. It looks ugly, but it works!
z_type Cip(z_type z) {return cos(z)/z;}
z_type Cipp(z_type z) {return (-sin(z) - cos(z)/z)/z ;}
z_type ACip0(z_type z) {z_type t=1./(z*z);
return (1.
+t*(-1./2.
+t*(13./24.
+t*(-541./720.
+t*(9509./8064.
+t*(-7231801./3628800.
+t*(1695106117./479001600.
+t*(-567547087381./87178291200.)))))))
)/z ; }
z_type ACip1(z_type z){int n; z_type c=ACip0(z);
c+=.1*(z-Cip(c))/Cipp(c) ;
c+=.2*(z-Cip(c))/Cipp(c) ;
c+=.3*(z-Cip(c))/Cipp(c) ;
c+=.4*(z-Cip(c))/Cipp(c) ;
c+=.5*(z-Cip(c))/Cipp(c) ;
c+=.7*(z-Cip(c))/Cipp(c) ;
DO(n,8) c+=(z-Cip(c))/Cipp(c) ;
return c;
} // ACip0 does not know about the singulatiry.
z_type acos(z_type z){
if(Im(z)<0){if(Re(z)>=0){return -I*log( z + sqrt(z*z-1.) );}
else{return -I*log( z - sqrt(z*z-1.) );}}
if(Re(z)>=0){return I*log( z + sqrt(z*z-1.) );}
else {return I*log( z - sqrt(z*z-1.) );} }
z_type ACipb(z_type z){ z_type t = 0.33650841691839534 + z ; z_type u=sqrt(t);
return
2.798386045783887
+u*(-2.437906425896532
+u*(0.7079542331649882
+u*(-.5009330133042798
+u*(0.5714459932734446
)))); }
z_type ACip3(z_type z){int n; z_type c=ACipb(z);
c+=.2*(z-Cip(c))/Cipp(c) ;
c+=.5*(z-Cip(c))/Cipp(c) ;
DO(n,8) c+=(z-Cip(c))/Cipp(c) ;
// DO(n,8) c=acos(c*z) ;
// DO(n,8) c=cos(c)/z ;
return c;
}
z_type ACip4(z_type z){int n; z_type z1=z_type(0,1.62134794610324);
z_type t=z-z1;
z_type c;
c=-z1+2.*sqrt(I*t);
// c=z1+t*(-2.+t*z_type(0,4.) );
c+=.2*(z-Cip(c))/Cipp(c) ;
c+=.5*(z-Cip(c))/Cipp(c) ;
DO(n,8) c+=.9*(z-Cip(c))/Cipp(c) ;
return c;
}
z_type ACip5(z_type z){int n;
if(Re(z)>0 && abs(z)>1.2) return ACip1(z);
if(Re(z)>-2 && fabs(Im(z))<1.) return ACip3(z);
if(Im(z)>0) return ACip4(z);
return conj(ACip4(conj(z)));
}
C++ generator of curve
Fiels ado.cin and acip.cin should be loaded at the working directory for compilation of the code below:
#include <math.h>
#include <stdio.h>
#include <stdlib.h>
#define DB double
#define DO(x,y) for(x=0;x<y;x++)
using namespace std;
#include <complex>
typedef complex<double> z_type;
#define Re(x) x.real()
#define Im(x) x.imag()
#define I z_type(0.,1.)
#include "ado.cin"
#include "acip.cin"
#define M(x,y) fprintf(o,"%6.4f %6.4f M\n",0.+x,0.+y);
#define L(x,y) fprintf(o,"%6.4f %6.4f L\n",0.+x,0.+y);
#define S(x,y) fprintf(o,"S\n",);
main(){ int j,k,m,n; DB x,y, p,q, t; z_type z,c,d;
DB y1= 1.1996786402577337;
DB zL= 2.798386045783887;
DB fL= -0.33650841691839534;
FILE *o;o=fopen("aciplot.eps","w");ado(o,320,330);
fprintf(o,"60 10 translate\n 100 100 scale\n");
for(m=0;m<4;m++){M(m,0)L(m,3)}
for(n=0;n<4;n++){M(-.5,n)L(2.5,n)}
fprintf(o,"2 setlinecap .01 W 0 0 0 RGB S\n");
for(m=-1;m<3;m++){M(.5+m,0)L(.5+m,3)}
for(n=0;n<4;n++){M(-.5,n+.5)L(2.5,n+.5)}
fprintf(o,"2 setlinecap .005 W 0 0 0 RGB S\n");
M(fL,zL)
DO(m,2901){ x=-.336+.001*m; z=x; y=Re(ACip5(z)); L(x,y) }
fprintf(o,"1 setlinejoin 1 setlinecap .02 W .7 0 0 RGB S\n"); p=1.8;q=.7;
M(fL,0)L(fL,zL)L(0,zL)
fprintf(o,"2 setlinecap .003 W 0 0 0 RGB S\n");
fprintf(o,"showpage\n%c%cTrailer",'%','%'); fclose(o);
system("epstopdf aciplot.eps");
system( "open aciplot.pdf");
getchar(); system("killall Preview");//for mac
}
Lated generator of lables
File aciplot.pdf ahould be generated with the code above before to compile the Latex document below.
% Copyleft 2012 by Dmitrii Kouznetsov %<br> \documentclass[12pt]{article} %<br> \usepackage{geometry} %<br> \usepackage{graphicx} %<br> \usepackage{rotating} %<br> \paperwidth 610pt %<br> \paperheight 610pt %<br> \topmargin -92pt %<br> \oddsidemargin -106pt %<br> \textwidth 900pt %<br> \textheight 900pt %<br> \pagestyle {empty} %<br> \newcommand \sx {\scalebox} %<br> \newcommand \rot {\begin{rotate}} %<br> \newcommand \ero {\end{rotate}} %<br> \newcommand \ing {\includegraphics} %<br> \begin{document} %<br> \parindent 0pt \sx{2}{ \begin{picture}(340,310) %<br> %\put(4,6){\ing{acosplot}} %<br> \put(4,6){\ing{aciplot}} %<br> \put(66,306){\sx{2}{$y$}} %<br> \put(42,290){\sx{2}{$f_0$}} %v \put(66,210){\sx{2}{\bf 2}} %<br> \put(66,110){\sx{2}{\bf 1}} %<br> \put(21, 21){\sx{2.1}{$z_0$}} %<br> \put(58, 19){\sx{2}{\bf 0}} %<br> \put(158, 19){\sx{2}{\bf 1}} %<br> \put(258, 19){\sx{2}{\bf 2}} %<br> \put(300, 21){\sx{2.1}{$x$}} %<br> \put(168,94){\sx{1.6}{\rot{-16}$y\!=\!\mathrm{ACip}(x)$\ero}} \end{picture} %<br> } %<br> \end{document}
File history
Click on a date/time to view the file as it appeared at that time.
| Date/Time | Thumbnail | Dimensions | User | Comment | |
|---|---|---|---|---|---|
| current | 17:50, 20 June 2013 | 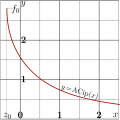 | 1,267 × 1,267 (84 KB) | Maintenance script (talk | contribs) | Importing image file |
You cannot overwrite this file.
File usage
The following page uses this file: