Superfunctions
«Superfunctions» is book about evaluation of abelfunctions, superfunctions, and the non-integer iterates of holomorphic functions. In particular, results for tetration, arctetration and iterates of exponential are presented.
The book is available at https://www.morebooks.de/store/gb/book/superfunctions/isbn/978-620-2-67286-3
The Book is loaded also as
https://mizugadro.mydns.jp/BOOK/466.pdf
[1]
There is also Russian version "Суперфункции" (y. 2014) [2]
Contents
Covers
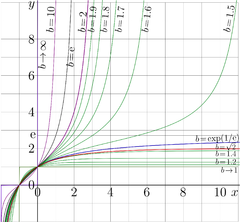
Explicit plot: tetration. \(y=\mathrm{tet}_b(x)\) for various \(b\!>\!1\), Fig.17.1
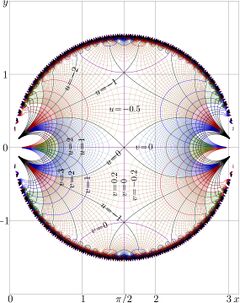
Complex map: truncated Taylor expansion of abelsine AuSin, Fig.22.2
At the front cover, the complex map of natural tetration is shown.
The following topics are indicated:
Non-integer iterates of holomorphic functions.
Tetration and other superfunctions.
Formulas, algorithms, tables, graphics and complex maps.
The back cover suggests short abstract of the Book and few notes about the Author.
About the topic
Assume some given holomorphic function \(T\). The superfunction is holomorphic solution \(F\) of equation \(T(F(z))=F(z+1)\)
The Abel function (or abelfunction) is the inverse of superfunction, \(G=F^{-1}\)
The abelfunction is solution of the Abel equation \(G(T(z))=G(z)+1\)
Additional conditions are considered to provide uniqueness of the solution \(F\) (and uniqueness of \(G\)).
As the superfunction \(F\) and the abelfunction \(G=F^{-1}\) are established, the \(n\)th iterate of transfer function \(T\) can be expressed as follows: \(T^n(z)=F(n+G(z))\)
This expression allows to evaluate the non-integer iterates. The number n of iterate can be real or even complex. In particular, for integer \(n\), the iterates have the common meaning: \(T^{-1}\) is inverse function of \(T\),
\(T^0(z)=z\),
\(T^1(z)=T(z)\),
\(T^2(z)=T(T(z)) \),
\(T^3(z)=T(T(T(z))) \),
and so on. The group property holds: \(T^m(T^n(z))=T^{m+n}(z)\)
The book is about evaluation of the superfunction \(F\), the abelfunction \(G\) and the non-integer iterates of various transfer functions \(T\).
The special notation is used in through the book; the number of iterate is indicated as superscript. For example,
In these notations, \(\sin^2(z)=\sin(\sin(z))\), but never \(\sin(z)^2\).
This notation is borrowed from the Quantum mechanics, where \(P^2(\psi)=P(P(\psi))\), but never \(P(\psi)^2\).
About the Book
Tools for evaluation of superfunctions, abelfunctions and non-integer iterates of holomorphic functions are collected. For a given transfer function T, the superfunction is solution F of the transfer equation F(z+1)=T(F(z)) . The abelfuction is inverse of F. In particular, the superfunctions of factorial, exponent, sin; the holomorphic extensions of the logistic sequence and of the Ackermann functions are suggested. From ackermanns, the tetration (mainly to the base b>1) and pentation (to base e) are presented. The efficient algorithm for the evaluation of superfunctions and abelfunctions are described. The graphics and complex maps are plotted. The possible applications are discussed. Superfunctions significantly extend the set of functions that can be used in scientific research and technical design. Generators of figures are loaded to the site TORI, http://mizugadro.mydns.jp for the free downloading. With these generators, the Readers can reproduce (and modify) the figures from the Book. The Book is intended to be applied and popular. I try to avoid the complicated formulas, but some basic knowledge of the complex arithmetics, Cauchi integral and the principles of the asymptotical analysis should help at the reading.
About the Author
Dmitrii Kouznetsov
Graduated from the Physics Department of the
Moscow State University (1980). Work: USSR, Mexico, USA, Japan.
Century 20: Proven the
quantum stability of the optical soliton, suggested
the low bound of the quantum noise of nonlinear
amplifier, indicated the limit of the single mode
approximation in the quantum optics.
Century 21:
Theorem about boundary behaviour of modes of Dirichlet laplacian,
Theory of ridged atomic mirrors, Formalism of superfunctions, TORI axioms.
Summary
The summary suggests main notations used in the Book:
\(T\)\( ~ ~ ~ ~ ~\) Transfer function
\(T\big(F(z)\big)=F(z\!+\!1)\) \(~ ~ ~\) Transfer equation, superfunction
\(G\big(T(z)\big)=G(z)+1\) \(~ ~ ~\) Abel equation, abelfunction
\(F\big(G(z)\big)=z\) \(~ ~ ~ ~ ~\) Identity function
\(T^n(z)=F\big(n+G(z)\big)\) \(~ ~ ~\) \(n\)th iterate
\(\displaystyle F(z)=\frac{1}{2\pi \mathrm i} \oint \frac{F(t) \, \mathrm d t}{t-z}\) \(~ ~ ~\) Cauchi integral
\(\mathrm{tet}_b(z\!+\!1)=b^{\mathrm{tet}_b(z)}\) \(~ ~ ~\) tetration to base \(b\)
\(\mathrm{tet}_b(0)=1\) \(~, ~ ~\) \( \mathrm{tet}_b\big(\mathrm{ate}_b(z)\big)=z\)
\(\mathrm{ate}_b(b^z)=\mathrm{ate}_b(z)+1\) \(~ ~\) arctetration to base \(b\)
\(\exp_b^{~n}(z)=\mathrm{tet}_b\big(n+\mathrm{ate}_b(z)\big)\) \(~ ~\) \(n\)th iterate of function \(~\) \(z\!\mapsto\! b^z\)
\(\displaystyle \mathrm{Tania}^{\prime}(z)=\frac{\mathrm{Tania}(z)}{\mathrm{Tania}(z)\!+\!1}\) \(~ ~\) Tania function,\(~\) \(\mathrm{Tania}(0)\!=\!1\)
\(\displaystyle \mathrm{Doya}(z)=\mathrm{Tania}\big(1\!+\!\mathrm{ArcTania}(z)\big)\) \(~ ~\) Doya function
\(\displaystyle \mathrm{Shoka}(z)=z+\ln(\mathrm e^{-z}\!+\!\mathrm e \!-\! 1)\) \(~\) Shoka function
\(\displaystyle \mathrm{Keller}(z)=\mathrm{Shoka}\big(1\!+\!\mathrm{ArcShoka}(z)\big)\) \(~ ~\) Keller function
\(\displaystyle \mathrm{tra}(z)=z+\exp(z)\) \(~ ~ ~\) Trappmann function
\(\displaystyle \mathrm{zex}(z)=z\,\exp(z)\) \(~ ~ ~ ~\) Zex function
\(\displaystyle \mathrm{Nem}_q(z)=z+z^3+qz^4\) \(~ ~ ~ ~\) Nemtsov function
Pictures
The pictures in the book are supplied with generators. The colleagues may download them, execute and reproduce the pics in *.eps and *.pdf format.
And, of course, modify them, adopt for the new similar problems.
The plotter of complex map conto.cin is original. It may have some bug(s), but still it seems to be best plotter for the complex maps, at least for year 2022. Any map from the Book can be generated in "real time".
The hand-drawn pics show connection of the topic of the book with the common sense of reality. They can be used also separately.
Recent advance
Most of results, presented in the book, are published in scientific journals; the links (without numbers) are supplied at the bottom.
After the appearance of the first version of the Book (2014), certain advances are observed about evaluation of tetration of complex argument; the new algorithm is suggested [3][4][5][6]. These results are not included in the book.
Refutation
Several transfer functions are considered in the book. I was searching for a transfer function such that for it, no suprefuction can be constructed. I failed. Perhaps, such a function does not exist. This can be considered as a conjecture.
If some colleague can prove this conjecture,
or refute it, id est, to construct such a function, for which the superfuntion cannot be constricted with methods, described in this Book –
then, please, publish your result and let me know (dmitriiKouznetsov(at)gmail.com),
in order that I can cite your publication here.
Misprints
| place | printed | should be |
|---|---|---|
| p.236, line 1 | In the movel | . In the novel |
| p.236, line 3 | 16.10 or 16.11, | (16.10) or (16.11), |
References
- ↑
https://mizugadro.mydns.jp/BOOK/466.pdf
D.Kouznetov. Superfunctions. 2020.
http://www.ils.uec.ac.jp/~dima/BOOK/443.pdf (its preliminary version)
- ↑
https://www.lap-publishing.com/catalog/details//store/gb/book/978-3-659-56202-0/Суперфункции
Дмитрий Кузнецов. Суперфункции.
ISBN-13: 978-3-659-56202-0
ISBN-10: 3659562025
EAN: 9783659562020
is loaded as
https://mizugadro.mydns.jp/BOOK/202.pdf
http://www.ils.uec.ac.jp/~dima/BOOK/202.pdf
- ↑ http://journal.kkms.org/index.php/kjm/article/view/428 William Paulsen. Finding the natural solution to f(f(x))=exp(x). Korean J. Math. Vol 24, No 1 (2016) pp.81-106.
- ↑ https://link.springer.com/article/10.1007/s10444-017-9524-1 William Paulsen, Samuel Cowgill. Solving F(z + 1) = b F(z) in the complex plane. Advances in Computational Mathematics, December 2017, Volume 43, Issue 6, pp 1261–1282
- ↑ https://search.proquest.com/openview/cb7af40083915e275005ffca4bfd4685/1?pq-origsite=gscholar&cbl=18750&diss=y Cowgill, Samuel. Exploring Tetration in the Complex Plane. Arkansas State University, ProQuest Dissertations Publishing, 2017. 10263680.
- ↑ https://link.springer.com/article/10.1007/s10444-018-9615-7 William Paulsen. Tetration for complex bases. Advances in Computational Mathematics, 2018.06.02.
The book combines the main results from the following publications:
http://www.ams.org/mcom/2009-78-267/S0025-5718-09-02188-7/home.html
http://mizugadro.mydns.jp/PAPERS/2009analuxpRepri.pdf
D.Kouznetsov. Analytic solution of F(z+1)=exp(F(z)) in complex z-plane. Mathematics of Computation 78 (2009), 1647-1670.
http://www.jointmathematicsmeetings.org/journals/mcom/2010-79-271/S0025-5718-10-02342-2/S0025-5718-10-02342-2.pdf
http://www.ams.org/journals/mcom/2010-79-271/S0025-5718-10-02342-2/home.html
http://eretrandre.org/rb/files/Kouznetsov2009_215.pdf
http://www.ils.uec.ac.jp/~dima/PAPERS/2010q2.pdf
http://mizugadro.mydns.jp/PAPERS/2010q2.pdf
D.Kouznetsov, H.Trappmann. Portrait of the four regular super-exponentials to base sqrt(2). Mathematics of Computation, 2010, v.79, p.1727-1756.
http://www.springerlink.com/content/qt31671237421111/fulltext.pdf?page=1
http://mizugadro.mydns.jp/PAPERS/2010superfae.pdf
D.Kouznetsov, H.Trappmann. Superfunctions and square root of factorial. Moscow University Physics Bulletin, 2010, v.65, No.1, p.6-12.
http://www.ils.uec.ac.jp/~dima/PAPERS/2010vladie.pdf
http://mizugadro.mydns.jp/PAPERS/2010vladie.pdf
D.Kouznetsov. Tetration as special function. Vladikavkaz Mathematical Journal, 2010, v.12, issue 2, p.31-45.
http://www.springerlink.com/content/qt31671237421111/fulltext.pdf?page=1
D.Kouznetsov, H.Trappmann. Superfunctions and square root of factorial. Moscow University Physics Bulletin, 2010, v.65, No.1, p.6-12
http://mizugadro.mydns.jp/t/index.php/Place_of_science_in_the_human_knowledge D.Kouznetsov. Place of science and physics in human knowledge. English translation from http://ufn.ru/tribune/trib120111 Russian Physics:Uspekhi, v.191, Tribune, p.1-9 (2010)
http://www.ils.uec.ac.jp/~dima/PAPERS/2010logistie.pdf http://mizugadro.mydns.jp/PAPERS/2010logistie.pdf D.Kouznetsov. Continual generalisation of the Logistic sequence. Moscow State University Physics Bulletin, 3 (2010) No.2, стр.23-30.
http://www.ams.org/journals/mcom/0000-000-00/S0025-5718-2012-02590-7/S0025-5718-2012-02590-7.pdf
http://www.ils.uec.ac.jp/~dima/PAPERS/2012e1eMcom2590.pdf
http://mizugadro.mydns.jp/PAPERS/2012e1eMcom2590.pdf
H.Trappmann, D.Kouznetsov. Computation of the Two Regular Super-Exponentials to base exp(1/e). Mathematics of Computation, 2012,
81, February 8. p.2207-2227.
http://www.ils.uec.ac.jp/~dima/PAPERS/2012or.pdf
http://mizugadro.mydns.jp/PAPERS/2012or.pdf
Dmitrii Kouznetsov. Superfunctions for optical amplifiers. Optical Review, July 2013, Volume 20, Issue 4, pp 321-326.
http://www.scirp.org/journal/PaperInformation.aspx?PaperID=36560
http://mizugadro.mydns.jp/PAPERS/2013jmp.pdf
D.Kouznetsov. TORI axioms and the applications in physics. Journal of Modern Physics, 2013, v.4, p.1151-1156.
http://www.ingentaconnect.com/content/asp/asl/2013/00000019/00000003/art00071 http://mizugadro.mydns.jp/PAPERS/2012thaiSuper.pdf D.Kouznetsov. Recovery of Properties of a Material from Transfer Function of a Bulk Sample (Theory). Advanced Science Letters, Volume 19, Number 3, March 2013, pp. 1035-1038(4).
http://link.springer.com/article/10.1007/s10043-013-0058-6 D.Kouznetsov. Superfunctions for amplifiers. Optical Review, July 2013, Volume 20, Issue 4, pp 321-326.
http://www.m-hikari.com/ams/ams-2013/ams-129-132-2013/kouznetsovAMS129-132-2013.pdf http://mizugadro.mydns.jp/PAPERS/2013hikari.pdf D.Kouznetsov. Entire function with logarithmic asymptotic. Applied Mathematical Sciences, 2013, v.7, No.131, p.6527-6541.
http://www.pphmj.com/references/8246.htm http://mizugadro.mydns.jp/PAPERS/2014susin.pdf D.Kouznetsov. Super sin. Far East Journal of Mathematical Science, v.85, No.2, 2014, pages 219-238.
https://arxiv.org/pdf/2208.05328.pdf James David Nixon. Asymptotic Solutions of the Tetration Equation. An analysis in the spirit of James Stirling. February 2022
Keywords
Abel function, Book, Doya function, Iteration, Keller function, Maple and tea, LambertW, Shoka function, Superfunction, SuperFactorial, SuSin, SuTra, SuZex, Tania function, Tetration, Trappmann function, Tetration, Zex function,


