Superfunction
For some holomorphic function \(T\) (called «Transfer function»), the Superfunction \(F\) is solution of the transfer equation
\[ F(z\!+\!1) = T(F(z)) \]
Formalism of superfunctions is described in special book «Superfunctions» (2020)
[1][2].
There is also Russian version «Суперфункции» (2014)
[3].
Superfunctions allow to constrict non-integer iterates of holomorphic functions; in particular, the square root of factorial \(\ \phi\!=\!\sqrt{\ !\ }\ \) as solution [4] of equation
\[ \phi(\phi(z))=z! \] and the «square root of exponential» [5] \(\ \varphi\!=\!\sqrt{\exp}\ \) as solution of equation \[ \varphi(\varphi(z))=\exp(z) \]
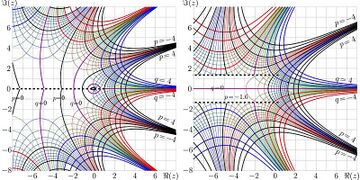
Maps of functions \(\phi\) and \(\varphi\) are shown in first figure.
For a given transfer function \(T\) and its superfunction \(F\), the inverses function \(G\!=\!F^{-1}\) is the Abelfunction. While for the Transfer function \(T\), the Superfunction \(F\) and the Abelfunction \(G\) are established, the \(n\)th iterate of the Transfer function can be expressed as follows:
\[ T^n(z)=F(n+G(z)) \]
In this expression, number \(n\) of iterate has no need to be integer; it can be real or even complex.
In such a way, with the superfunction and the Abelfunction, the transfer function can be iterated arbitrary times. To century 21, this property seems to provide the main application of superfunctions.
History
Functions \(\sqrt{\ !\ }\) and \(\sqrt{\exp} \) are mentioned century 20 as LOGO pf Physics Department of the Moscow State University [7][8][9] and as holomorphic solution of \(\varphi(\varphi(z))=\exp(z)\) [4] suggested by Hellmith Kneser, see pictures above.
In century 20, before construction of formalism of superfunctions, these functions were not implemented; the complex maps of these functions were not plotted, although many publications about non-integer iterates of functions are observed. The first robust implementations of non-trivial superfunctions and ablefunctions appear in years 2009-2010 [4]
Definition
The integer values of the argument, the superfunction has simple sense.
For some constant \(t\), the superfunction \(F\) can be expressed as follows: \(\displaystyle {{F(z)} \atop \,} {= \atop \,} {T^z(t) \atop \,} {= \atop \,} {{\underbrace{T\Big(T\big(... T(t)...\big)\Big)}} \atop {z \mathrm{~evaluations~of~function~}T\! \!\!\!\!\!}}\)
In general case, the Superfunction can be defined as follows:
For complex numbers \(~p~\) and \(~q~\), such that \(~p~\) belongs to some connected domain \(D\subseteq \mathbb{C}\),
superfunction (from \(p \mapsto q\)) of holomorphic function \(~T~\) on domain \(C \in \mathbb C\) is
function \( F \), holomorphic on domain \(D\), such that
\[F(z\!+\!1)=T(F(z)) ~ \forall z\in D : z\!+\!1 \in D\]
\[F(p)=q\]
Uniqueness
In general, for a given holomorphic transfer function \(T\), the superfunction \(F\) is not unique, even is some specific value \(F(0)\) is fixed.
Other superfunctions \(f\) can be constructed as follows:
\[ f(z)=F(z+\theta(z)) \] where \(\theta\) is any periodic holomorphic periodic function with period unity.
The \(\theta\) can be represented as sum of sinusoids,
\[ \theta(z)= \sum_{k=1}^{\infty} a_k \sin(2\pi k z) \]
with some real coefficients \(a\); such a representation converts the real-holomorphic superfunction \(F\) to another real-holomorphic superfunction \(f\), and even preserves the value at zero; \[ f(0)=F(0) \]
However, each sin in this representation shows fast growth in the direction of imaginary axis.
If we fix the asymptotic behavior at \(\pm \mathrm i\infty\)
then we may hope the solution \(F\) of the transfer equation to be unique.
In particular for the natural Tetration, it is postulated, that at \(\pm \mathrm i\infty\), this the superfunction approaches the fixed points \(L\) and \(L^*\) of natural logarithm; \[ L = -\mathrm{ProductLog}(-1)^* \approx 0.3181315052047641+ 1.3372357014306895 \mathrm{I} \] This requirement not only provides the uniqueness of the tetration [10], but also gives the way for the efficient evaluation through the Cauchi intergal and/or the asymptotic expansion of tetration at \(\pm \mathrm i\infty\) [11] and the fast precise numerical implementation [12].
Other meanings of the words
Mathematics often borrow terms from the common life. This may cause confieions. In particular this applies to terms Superfunciton and Nest. Few examples are shown in figures at right.
Not all supperfunctions are holomorphic.
Some Nests may be difficult to implement in Mathematica.
Even term Superpower may have different meanings.
In TORI there terms are not used in sense shown in figures at right.
References
- ↑ https://www.amazon.co.jp/Superfunctions-Non-integer-holomorphic-functions-superfunctions/dp/6202672862 Dmitrii Kouznetsov. Superfunctions: Non-integer iterates of holomorphic functions. Tetration and other superfunctions. Formulas,algorithms,tables,graphics – 2020/7/28
- ↑ https://mizugadro.mydns.jp/BOOK/468.pdf Dmitrii Kouznetsov (2020). Superfunctions: Non-integer iterates of holomorphic functions. Tetration and other superfunctions. Formulas, algorithms, tables, graphics. Publisher: Lambert Academic Publishing.
- ↑ https://mizugadro.mydns.jp/BOOK/202.pdf Дмитрий Кузнецов. Суперфункции. Lambert Academic Publishing, 2014
- ↑ 4.0 4.1 4.2 4.3 4.4
https://link.springer.com/article/10.3103/S0027134910010029
https://mizugadro.mydns.jp/PAPERS/2010superfae.pdf D.Kouznetsov, H.Trappmann. Superfunctions and square root of factorial. Moscow University Physics Bulletin, 2010, v.65, No.1, p.6-12. (Russian version: p.8-14) - ↑ http://www.digizeitschriften.de/dms/img/?PID=GDZPPN002175851&physid=phys63#navi Hellmuth Kneser. Reelle analytische Lösungen der Gleichung \( \varphi(\varphi(x))=\mathrm e^x \) und verwandter Funktionalgleichungen. Journal für die reine und angewandte Mathematik / Zeitschriftenband (1950) / Artikel / 56 - 67
- ↑ https://opc.mfo.de/detail?photo_id=7607 On the Photo: Kneser, Hellmuth Location: Oberwolfach Author: Danzer, Ludwig (photos provided by Danzer, Ludwig) Source: L. Danzer, Dortmund Year: 1958 Copyright: L. Danzer, Dortmund Photo ID: 7607
- ↑ (not available: http://ofvp.phys.msu.ru/pdf/Kandidov_70.pdf ) V.P.Kandidov. About the time and myself. (In Russian) 2007.05.18. .. По итогам студенческого голосования победителями оказались значок с изображением рычага, поднимающего Землю, и нынешний с хорошо известной эмблемой в виде корня из факториала, вписанными в букву Ф. Этот значок, созданный студентом кафедры биофизики А.Сарвазяном, привлекал своей простотой и выразительностью. Тогда эмблема этого значка подверглась жесткой критике со стороны руководства факультета, поскольку она не имеет физического смысла, математически абсурдна и идеологически бессодержательна. ..
- ↑ https://www.nkj.ru/archive/articles/1023/ V.Sadovnichi. 250 anniversary of the Moscow State University. (In Russian) В. Садовничий. ПЕРВОМУ УНИВЕРСИТЕТУ СТРАНЫ - 250! НАУКА И ЖИЗНЬ, №1, 2005. .. На значке физфака в букву "Ф" вписано стилизованное изображение корня из факториала (√!) - выражение, математического смысла не имеющее. ..
- ↑ Logo of the Physics Department of the Moscow State University. (In Russian); http://zhurnal.lib.ru/img/g/garik/dubinushka/index.shtml
- ↑
https://link.springer.com/article/10.1007/s00010-010-0021-6
http://mizugadro.mydns.jp/PAPERS/2011uniabel.pdf H.Trappmann, D.Kouznetsov. Uniqueness of holomorphic Abel functions at a complex fixed point pair Aequationes Mathematicae, v.81, p.65-76 (2011) - ↑
http://www.ams.org/mcom/2009-78-267/S0025-5718-09-02188-7/home.html
http://mizugadro.mydns.jp/PAPERS/2009analuxpRepri.pdf D.Kouznetsov. Analytic solution of F(z+1)=exp(F(z)) in complex z-plane. Mathematics of Computation, v.78 (2009), 1647-1670. - ↑
http://www.vmj.ru/articles/2010_2_4.pdf
http://mizugadro.mydns.jp/PAPERS/2009vladie.pdf D.Kouznetsov. Tetration as special function. Vladikavkaz Mathematical Journal, 2010, v.12, issue 2, p.31-45. - ↑ https://endless-sport.co.jp/products/suspension/index_superfunction.html Functionメーカー別適合表 ホーム> サスペンショントップ Super Function / スーパーファンクション(サーキット向け)(2020).
- ↑ https://www.pythonforbeginners.com/super/working-python-super-function Working with the Python Super Function. Last Updated: May 20, 2020. Python 2.2 saw the introduction of a built-in function called “super,” which returns a proxy object to delegate method calls to a class – which can be either parent or sibling in nature.
http://www.proofwiki.org/wiki/Definition:Superfunction
http://en.citizendium.org/wiki/Superfunction
2014. https://www.morebooks.de/store/ru/book/Суперфункции/isbn/978-3-659-56202-0 Dmitrii Kouznetsov. Суперфункции. Lambert Academic Publishing, 2014. (In Russian)
2016. https://doi.org/10.11568/kjm.2016.24.1.81 W.Paulsen, “FINDING THE NATURAL SOLUTION TO f(f(x)) = exp(x),” Korean Journal of Mathematics, vol. 24, no. 1, pp. 81–106, Mar. 2016.
2017. https://search.proquest.com/openview/cb7af40083915e275005ffca4bfd4685/1 S.Cowgill. Exploring Tetration in the Complex Plane. Arkansas State University, ProQuest Dissertations Publishing, 2017. 10263680.
2017. https://doi.org/10.1007/s10444-017-9524-1 W.Paulsen, S.Cowgill, Solving F(z + 1) = b ^ F(z) in the complex plane. Adv Comput Math 43, 1261–1282 (2017).
2018. https://doi.org/10.1080/10236198.2017.1307350 M.H. Hooshmand. (2018) Ultra power of higher orders and ultra exponential functional sequences. Journal of Difference Equations and Applications. Volume 24, 2018 - Issue 5: Special Issue: European Conference on Iteration Theory 2016. Special Issue Editors: Marek Cezary Zdun & Jaroslav Smital.
2019. https://doi.org/10.1007/s10444-018-9615-7 W.Paulsen. Tetration for complex bases. Adv Comput Math 45, 243–267 (2019).
2020. https://www.morebooks.de/store/gb/book/superfunctions/isbn/978-620-2-67286-3 D.Kouznetsov. Superfunctions. Lambert Academic Publishing, 2020.
Keywords
«Abel function», «Iteration», «Regular iteration», «SuperFactorial», «Superfunctions», «Transfer function», «Transfer equation», «Tetration», «Tania function», «Tania function», «Shoka function», «SuZex», «SuTra».
«Суперфункции»,



