Iteration

Iteration , or iterate (итерация) is function, expressed as repetition of another (iterated) function, that may be called iterand.
Any function by itself is considered as its first iteration.
The zeroth iteration of any non-trivial function is supposed to be Identity function.
The minus first iteration of a function is its inverse function
Iteration of a function \(T\) can be denoted with superscript [1]; \(T^n\) means the \(n\)th iteration of function \(T\), id est,
\(\displaystyle {{T^n(z)}\atop{\phantom{sub}}} {{=}\atop{\phantom{sub}}}{{\underbrace{T\!\Big(T\!\big( .. T(z).. \big)\Big)}}\atop{n ~\mathrm{evaluations~of~ function~} T}}\)
This may be expressed with equations
\(~T^0(z)\!=\!z~\), \(~ T^n(z)=T\Big( T^{n-1}(z) \Big)~\) for \(n\! > \!0\)
Similar notations, where the superscript is used to indicate the number of iterate is used also in quantum mechanics and the linear impulsive control [2]. For iteration of functions, the same notation is used also by Walter Bergweiler [3].
Term iteration may have also another meaning, indicating repetition of some process (even if such a repetition does not define a new function).
Physical sense
If \(T\) is transfer function of some device, say, amplifier, then, the transfer function of combination of two such devices can be expressed as \(T^2\); and the transfer function of combination of \(n\) identical devices can be written as \(T^n\) [4].
Nest
In Mathematica, the special operation is incorporated, called Nest. Usually, Nest has 3 arguments. The first argument is name of iterand, which is function. The second argument is initial value of the iterations, and the last argument is number of iteration. With Nest, the iteration of function \(f\) can be written as follows:
\( f^n(z)=\mathrm{Nest}[f,z,n]\)
In Mathematica, all arguments of all functions should be written in squared parenthesis. Up to year 2012, the Nest is implemented only for the cases, when number \(n\) of iterations can be simplified to a natural number, expressed with integer constant. Attempts to call Nest to evaluate a non–integer iterate of a function are interpreted as error.
Non–integer iterate
The non–integer iterate is simple and obvious in the case when the iterand is linear function; then the iteration can be expressed through the elementary function. Let \(T(z)=a+b z~\). Then
\(\displaystyle T^n(z)=a \frac{1\!-\!b^n}{1\!-\!b} + b^n z\)
This expression allows the straightforward interpretation for non–integer \(n\). For fixed \(n\) and \(b\), this is linear function.
The case of power function is also simple. Let \(T(z)=z^a\), where \(a\!>\!1\).
Then \(T^n(z)\!=\!z^{a^n}\).
In this expression, \(n\) has no need to be integer.
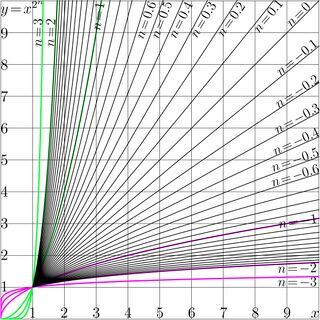
For \(a\!=\!2\), the iterations of quadratic function are shown in Figure 1.
For more general case, the non–integer iterates of a function \(T\) can be defined through its superfunction \(F\) and the Abel function \(G\!=\! F^{-1}\); the iterand \(T\) is treated as the transfer function, and the superfunction \(F\) satisfies the transfer equation
\(F(z\!+\!1)=T\!\Big( F(z) \Big)\)
Then, the \(n\)th iteration of the transfer function can be expressed as
\(T^n(z)=F\Big(n+G(z) \Big)\)
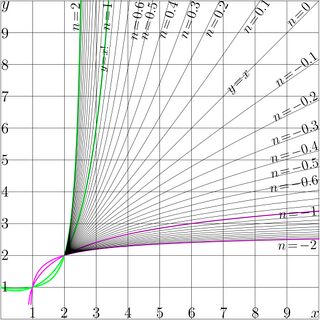
In this expression, parameter \(n\) also has no need to be integer. Once holomorphic functions \(F\) and \(G\) are established, the function can be iterated even complex number of times. For a given transfer function \(T\), the establishment of the superfunction \(F\) and the Abel function \(G\) is not trivial, but solvable problem. It had been formulated in 1950 by Hellmuth Kneser [5] for iterates of exponential, the half-iterate of the exponential appears in the title of his article. In century 21, superfunctions of various funcitons had been calculated, allowing the non-integer iterates. The iterates of Factorial are plotted in figure 2; and those for the exponential [6][7]; are shown in Figure 3. Then, the formalism had been extended to other functions [8][9][4], in particular, to the exponentials to other bases, factorial and the logistic sequence.
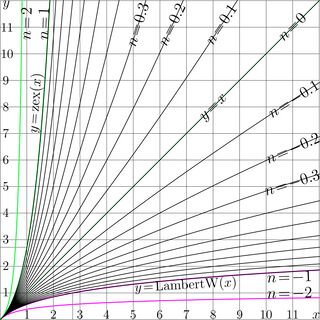
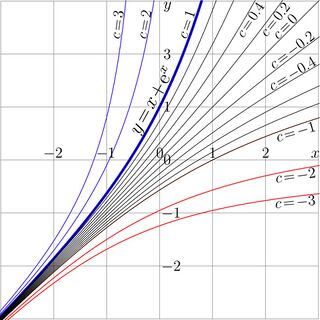
For the non–integer iterates, it should be assumed that \(T\) is holomorphic function, and the superfunction \(G\) is also expected to be holomorphic. In order to provide uniqueness of the superfunction, the certain requirements on its behavior should be assumed. Usually, \(F\) approaches some fixed points of function \(T\) at infinity (see the special articles Superfunction and Abel function). Henryk Trappmann had suggested an example of a transfer function that has no fixed points, namely, the Trappmann function, \(\mathrm{tra}(z)=z\!+\!\mathrm e^z\). Such a transfer function was supposed to be difficult to iterate. However, the superfunction (id est, "SuperTrappmann") can be expressed through that for function zex, \(\mathrm{zex}(z)\!=\!z\exp(z)\), and then the "SuperTrappmann" can be called simply hen, and the iterate can be expressed as usually through the hen and the "AbelTrappmann" ahe\(~=\mathrm{hen}^{-1}\). The iterates of zex are shown in Figure 3, and the iterates of the Trappmann function tra are shown in Figure 4.
It seems, that the non-integer iterates can be defined for any holomorphic function, but the rigorous mathematical proof of such conjecture is required.
In some cases, the non–integer iterate can be defined also throgh the Schroeder function, but the representation through the Superfunction and the Abel function seems to be more universal.
In general, the non-integer iterate is not unique, and the specific behavior of the superfunction \(F\) should be assumed for the unigieness.
Examples
This section offers a little bit more detailed description of figures, mentioned above.
Elementary functions
No pics for the elementary functions of this subsection are loaded; it is assumed that everyone can plot then without assistance
Let
\(\displaystyle T(z)\!=\! \frac{a^2+(2a\!+\!b)z}{b-z}\)
The corresponding superfunction and Abel function are
\(\displaystyle F(z)=\frac{ a z \!+\! b}{1\!-\! z}~\), \(~ \displaystyle G(z)=\frac{ z \!-\! b}{a\!+\! z}\)
give the iterate
\(\displaystyle T^n(z)\!=\! \frac{a^2+\Big(a(1\!+\!n)+b\Big)z}{a+b- a n- n z}\)
More "solvable" tranfer functions can be constructed using Table of superfunctions.
However, for some cases the solution cannot be simply expressed with elementary functions. Few of them are mentioned below.
Special functions
Figure 1 shows iterates of quadratic function, \(~T(z)\!=\!z^2~\). In this case, the \(n\)th the iterate \(~T^n(z)\!=\!z^{2^n}~\) can be expressed through the power function.
Figure 2 shows iterates of the exponential, \(~T(z) \!=\! \exp(z)\). In this case, for non-integer \(n\), the \(n\)th iterate
\(~T^n(z)\!=\! \mathrm{tet}\Big(n\!+\!\mathrm{ate}(z)\Big)~\) is expressed through tetration tet and ArcTetration ate, and cannot be easy represented through elementary functions.
Figure 3 shows iterates of function zex, \(~T(z)\!=\! \mathrm{zex}(z)\!=\!z \exp(z)~\). In this case, for non–integer \(n\), the \(n\)th iterate
\(~T^n(z)\!=\! \mathrm{SuZex}\Big(n\!+\!\mathrm{AuZez}(z)\Big)~\)
can be expressed through functions SuZex and AuZex, which are, of course, superfunction and Abel function for the transfer function zex.
Figure 4 shows iterates of function Zex, \(~T(z)\!=\!\mathrm{zex}(z)\!=\!z\, \exp(z)~\). n this case, for non–integer \(n\), the \(n\)th iterate
\(~T^n(z)\!=\!\mathrm{zex}^n(z)\!=\! \mathrm{SuZex}\Big(n\!+\!\mathrm{AuZex}(z)\Big)~\)
Figure 5 shows iterates of the Trappmann function, \(~T(z)\!=\!\mathrm{Tra}(z)\!=\!z\!+\!\exp(z)~\). In this case, for non–integer \(n\), the \(n\)th iterate
\(~T^n(z)\!=\!\mathrm{tra}^n(z)\!=\! \mathrm{SuTra}\Big(n\!+\!\mathrm{AuTra}(z)\Big)~\)
is expressed through the functions SuTra and AuTra, but, perhaps, cannot be easy represented through elementary functions. However functions SuTra and AuTra can be expressed in terms of SuZex and AuZex mentioned above in the following way:
\(\mathrm{SuTra}(z)=\ln\Big(\mathrm{SuZex}(z)\Big)\)
and
\(\mathrm{AuTra}(z)=\mathrm{AuZex}\Big(\exp(z)\Big)\)
However, function SuTra can be implemented even without use of function SuZex; the description of this implementation is published in 2013 [10].
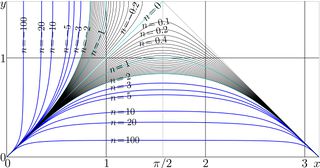
Figure 6 shows iterats of sin. These iterates are expressed through functions SuSin and AuSin; \( \sin^n(z)=\mathrm{SuSin}\big(n+\mathrm{AuSin}(z)\big)\)
The number of examples can be greatly extended, using the Table of superfunctions, that offers triads \(T,F,G\), and general expression \(T^n(z)=F\Big(n\!+\!G(z)\Big)\). In this way, one can plot the iterates of exponential to various bases, iterates of factorial, iterates of the logistic operator, and iterates of any functions, assuming, that we can choose the appropriate superfunction and the Abel function. In principle, any holomorphic function can be iterated any number \(n\) of times, even complex number of times.
General cases
For general transfer function \(T\), the non-integer iterates can be constructed in various ways. In TORI, the heneral method with superfunctions is generally used. In many cases, when the real-holomorphic transfer function has a real fixed point, its iterates can be expressed through the Schroeder function and its inverse [11]
Discussion
Due to the heavy traffic of the destructive bots and tricky trolls, the writing access in TORI is suspended. The most of content of this article is available at Citizendium [12] and can be discussed (and criticized and corrected) there. Discussion through the email is also welcomed.
References
- ↑ http://www.ams.org/journals/bull/1993-29-02/S0273-0979-1993-00432-4/S0273-0979-1993-00432-4.pdf Walter Bergweiler. Iteration of meromorphic functions. Bull. Amer. Math. Soc. 29 (1993), 151-188
- ↑ http://www.sciencedirect.com/science/article/pii/S0895717704905225 XINZHI LIU. Stability of Impulsive Control Systems with Time Delay. Mathematical and Computer Modelling 39 (2004) 511-519. .. \(A^{1/2}\) denotes the square root of \(A\), which is defined to be the unique positive definite matrix satisfying \(A^{1/2} \cdot A^{1/2} = A\)
- ↑ http://www.ams.org/journals/bull/1993-29-02/S0273-0979-1993-00432-4/S0273-0979-1993-00432-4.pdf W.Bergweiler. Iteration of meromorphic functions. Bulletin (New Series) of the American Mathematical society, v.29, No.2 (1993) p.151-188.
- ↑ 4.0 4.1
http://www.springerlink.com/content/qt31671237421111/fulltext.pdf?page=1
http://mizugadro.mydns.jp/PAPERS/2010superfae.pdf D.Kouznetsov, H.Trappmann. Superfunctions and square root of factorial. Moscow University Physics Bulletin, 2010, v.65, No.1, p.6-12. (Russian version: p.8-14) - ↑ http://mizugadro.mydns.jp/PAPERS/Relle.pdf H.Kneser. "Reelle analytische Loesungen der Gleichung \(\phi(\phi(x))=\mathrm e^x\) und verwandter Funktionalgleichungen". Journal fur die Reine und Angewandte Mathematik 187 (1950): 56-67.
- ↑ http://www.ams.org/mcom/2009-78-267/S0025-5718-09-02188-7/home.html Preprint: http://www.ils.uec.ac.jp/~dima/PAPERS/2009analuxpRepri.pdf D.Kouznetsov. Analytic solution of F(z+1)=exp(F(z)) in complex z-plane. Mathematics of Computation, v.78 (2009), 1647-1670.
- ↑ http://mizugadro.mydns.jp/PAPERS/2010vladie.pdf D.Kouznetsov. Superexponential as special function. Vladikavkaz Mathematical Journal, 2010, v.12, issue 2, p.31-45.
- ↑ http://www.ams.org/journals/mcom/2010-79-271/S0025-5718-10-02342-2/home.html http://mizugadro.mydns.jp/PAPERS/2010sqrt2.pdf http://mizugadro.mydns.jp/PAPERS/2010q2.pdf D.Kouznetsov, H.Trappmann. Portrait of the four regular super-exponentials to base sqrt(2). Mathematics of Computation, 2010, v.79, p.1727-1756.
- ↑ http://www.ams.org/journals/mcom/0000-000-00/S0025-5718-2012-02590-7/S0025-5718-2012-02590-7.pdf http://mizugadro.mydns.jp/PAPERS/2012e1eMcom2590.pdf H.Trappmann, D.Kouznetsov. Computation of the Two Regular Super-Exponentials to base exp(1/e). (Mathematics of Computation, 2012 February 8.) ISSN 1088-6842(e) ISSN 0025-5718(p)
- ↑
http://www.m-hikari.com/ams/ams-2013/ams-129-132-2013/kouznetsovAMS129-132-2013.pdf
http://mizugadro.mydns.jp/PAPERS/2013hikari.pdf D.Kouznetsov. Entire function with logarithmic asymptotic. Applied Mathematical Sciences, 2013, v.7, No.131, p.6527-6541. - ↑ http://arxiv.org/pdf/1002.0104v4.pdf Chaotic Maps, Hamiltonian Flows, and Holographic Methods. Thomas L. Curtright1 and Cosmas K. Zachos. 2010 September 10.
- ↑ http://en.citizendium.org/wiki/Iteration_of_function
http://www.ams.org/journals/bull/1993-29-02/S0273-0979-1993-00432-4/S0273-0979-1993-00432-4.pdf WALTER BERGWEILER. ITERATION OF MEROMORPHIC FUNCTIONS. Nilletin of the AMERICAN MATHEMATICALSOCIETY Volume29,Number2,October1993, p. 151-188.
Keywords
«Abel function», «Abel equation», «AuSin», «AuTra», «Doya function», «Regular iteration», «SuperFactorial», «Superfunction», «Superfunctions», «SuSin», «SuTra», «Tetration», «Transfer equation», «Keller function», «Trappmann function»,