Sin
Sin is solution \(f\) of the trigonometric differential equation
\(f''(z)+f(z)=0\)
with additional requirements
\(\sin(0)=0\)
\(\sin'(0)=1\)
Postulating properties of sin
In the courses for those students, who do not know, that character "prime" after the name of a function denotes its derivative, properties of function sin and cos were postulated through the Euclid axioms and the corresponding Pythagore theorem.
The postulating of some properties of some functions may have sense while no proof is available. Properties of functions sin and cos, can be deduced from the differential equation above. As less postulates are involved, the concept of sin as solution of the differential equation is simpler than the ratio of the cathetus to the hypothenuse used in the school courses of mathematics. According to the Sixths of the TORI axioms, the concept through the differential equation has the priority.
Properties of function sin are ton repeater here as they are listed at the common resources
http://en.citizendium.org/wiki/Sine
http://en.wikipedia.org/wiki/Sine
http://www.wolframalpha.com/input/?i=sin(x)
Representation through exponential
While function exp is already defined, function sin can be defined with
\(\displaystyle \sin(z)= \frac{\exp(\mathrm i z)-\exp(-\mathrm i z)}{2 ~ \mathrm i }\)
without deferring to the differential equation above.
Representation through SuSin and AuSin and iterations
Function sin can be represented through its superfunction and the corresponding Abel function, id set, through the super sin and the Abel sin.
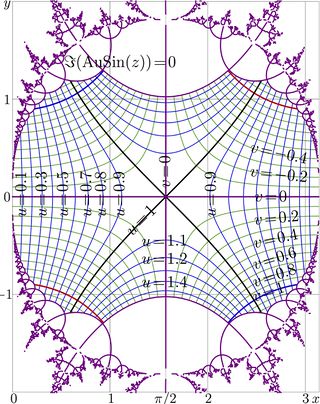
For sin as the transfer function, the superfunction is SuSin, and the corresponding Abel function is AuSin. Then, the \(n\)th iterate of function sin can be expressed as follows:
\( \sin^n(z)=\mathrm{SuSin}\big( n + \mathrm{AuSin}(z) \big)\)
In this expression, number \(n\) of iterate has no need to be integer. As other holomorphic functions, sin can be iterated any real or even complex number of times. However, the range of validity of the representation above is limited.
Range of validity of the representation of function sin above at \(n\!=\!1\) is shown in figure at right in the \(~z\!=\! x+\!\mathrm i y~\) complex plane. WIthin the range, the complex map of function sin is shown. The boundaries of the range of validity follow the lines \(~\Im\big(\mathrm{AuSin}(z)\big)\!=\!0~\); these lines are also drawn.
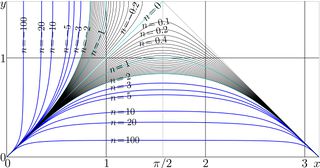
The representation above through AuSin and SuSin is used to plot the non0integer iterates of sin, shown in figure at right.
\(y=\sin^n(x)\)
is shown for various number \(n\) of iterates. The iterates for integer \(n\) are shown with thick lines. For moderate values of \(x\), the relation
\(\sin^m\big(\sin^n(x)\big)=\sin^{m+n}(x)\)
takes place. In particular, this relation is broken for \(x>\pi/2\), as the main branches of AuSin and SuSin do not return an approptiate values.
Curves similar to those in the figure at right had been presented in 2012 by Thomas Curtright, although no precise algorithm for the evaluation had been supplied [1]
References
- ↑ http://server.physics.miami.edu/~curtright/Schroeder.html Dr. Thomas Curtright. Continuous iterates continue to be interesting, after 150 years of study. (2012) As a first illustration, we display the continuous iterates of the sine function, sin[t](x). Note that the maximum values at x = π/2 are approximately given by exp[(1-√t) ln(π/2)].
http://mizugadro.mydns.jp/PAPERS/2014susinL.pdf official locked version
http://www.pphmj.com/references/8246.htm
http://mizugadro.mydns.jp/PAPERS/2014susin.pdf
D.Kouznetsov. Super sin. Far East Jourmal of Mathematical Science, v.85, No.2, 2014, pages 219-238.
http://mathoverflow.net/questions/45608/formal-power-series-convergence Formal power series convergence. edited Nov 13 '10 at 2:54. .. f(f(x))=sin x ..