AuSin
AuSin, is the Abel function for the primary elementary function known as sin.
AuSin is inverse function of SuSin, \(~\mathrm{AuSin}=\mathrm{SuSin}^{-1}\)
\(g=\mathrm{AuSin}~ ~\) is solution of the Abel equation
\(\mathrm{AuSin}(\sin(z))=\mathrm{AuSin}(z)+1\)
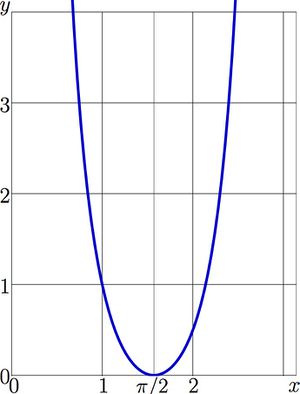
Explicit plot of function AuSin is shown in figure at right.
Properties of functions SuSin and AuSin are described in Far East Jourmal of Mathematical Science
[1], 2014 and also in book «Superfunctions»
[2], 2020.
Some of these properties are mentioned below.
Properties
As \(\mathrm{SuSin}(1)=1\), the inverse function at unity is also unity;
\(\mathrm{AuSin}(1)=1\)
Then, \(\mathrm{AuSin}(\pi/2)=\mathrm{AuSin}(\arcsin(1))=\mathrm{AuSin}(1)-1=0\)
Both the explicit plot of ArcSin and its map are symmetric with respect to reflection from the line \(x=\pi/2~\):
\(\mathrm{AuSin}(z)=\mathrm{AuSin}(\pi/2-z)\)
Expansion at \(\pi/2\)
Expansion at \(\pi/2\) has the following form:
\(\displaystyle \mathrm{AuSin}\left( \frac{\pi}{2}+t \right) = \sum_{n=1}^{\infty} b_n t^{2n}\)
The first coefficients \(b\) of this expansion are evaluated in the table below:
\(\displaystyle \begin{array}{cc} n & b_n\\ 1 & 2.29163807440958 \\ 2 & 1.96043852439688 \\ 3 & 1.07862851256147 \\ 4 & 0.59622997993395 \\ 5 & 0.28333997139829 \\ 6 & 0.14193261194548 \\ 7 & 0.06423734271234 \\ 8 & 0.03026687705508 \\ 9 & 0.01351721250427 \\ \end{array} \)
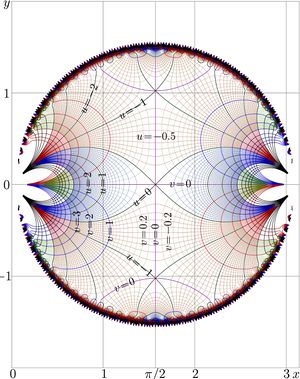
More coefficient are supplied in the Discussion. The series converges at \(~|t|\!<\!\pi/2~\). The map of approximation of AuTra with the truncated expansion with 40 terms is shown in the figure that is not yet loaded.
This expansion is good for evaluation of \(\mathrm{AuSin}(z)\) at \(\displaystyle \left| \frac \pi 2 - z \right|<1\)
with 40 terms taken into account, the truncated series returns of order of 14 significant figures.
Evaluation
Let
\(\displaystyle G_M(z)=\frac{3}{z^2}+\frac{5}{6} \ln(z)+ \sum_{m=1}^M c_m z^{2m} \)
Substitution of \(g(z)=G_M(z)+O(z^{2M+2})\) into the Abel equation with the transfer function sin
\(g(\sin(z))=g(z)+1\)
determines the coefficients \(c_1\), \(c_2\), ..These coefficients can be calculated with the substitution of the expansion to the Abel equation and the straightforward asymptotic analysis.
The first coefficients \(c\) are shown in the table below
\( \displaystyle\begin{array}{ccccccccccc} c_1 & c_2 & c_3& c_4& c_5& c_6 \\ \frac{79}{1050} & \frac{29}{2625} & \frac{91543}{36382500} & \frac{18222899}{28378350000} & \frac{88627739}{573024375000}& \frac{3899439883}{142468185234375} \end{array} \)
Then, function \(G\) can be evaluated with
\(\displaystyle G(z)=\lim_{k\rightarrow \infty} G_M\big(\sin^k(z)\big)-k\)
While \(G_M\) is asymptotic solution of the Abel equation with sin as the transfer function, the limit does not depend on \(M\); although, the rate of convergence improves with the increase of \(M\).
Then, thigough this \(G\), the Abel sin appears as
\(\mathrm{AuSin}(z)=G(z)-G(\pi/2)\)
in such a way that \(\mathrm{AuSin}(\pi/2)=0\) ; the constant \(G(\pi/2)\approx 2.089622719729524\)
Function AuSin has sense of number of iterates of sin, begining with \(\pi/2\), required in order to get value of argument. However, the number of these iterates has no need to be integer.
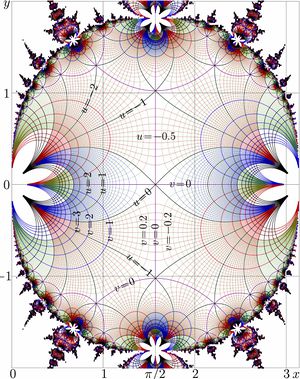
The numerical implementation of AuSin with the algorithm above is stored as ausin.cin. The area of agreement of this implementation with that of function SuSin is seen from the complex map of function \(\mathcal A(z)=\mathrm{SuSin}\big( \mathrm{AuSin}(z) \big)\) This map is not yet loaded.
The numerical implementation reproduces the relation \(\mathrm{AuSin}(\pi\!-\!z)\!=\!\mathrm{AuSin}(z)\) with 14 decimal figures at least within range \(\displaystyle \left| \frac{\pi}{2} - z \right| < \frac{\pi}{2} \)
Range of validity
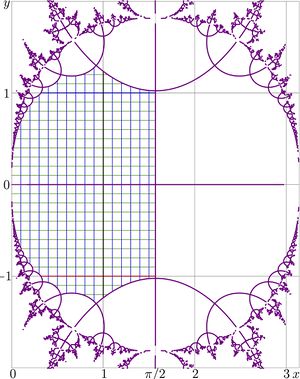
in the \(z\!=\!x\!+\!\mathrm i y\) plane]] In order to show the range of validity of relation
\( \mathrm{SuSin}\big(\mathrm{AuSin}(z)\big)=z\)
the map of the left hans side of this equation is shown, while the equation holds, in the figure at right (to be loaded) in the plane \(z\!=\!x\!+\!\mathrm i y\)
This map appears as a rectangular grid. The range of validity is bounded, surrounded by the lines
\(~\Im\big(\mathrm{AuSin}(z)\big)=0~\)
These lines are also drawn.
Iterations or sin
WIth SuSin and AuSin, Iterations of sin can be presented in the following way:
\(\sin^n(z)=\mathrm{SuSin}(n+\mathrm{AuSin}(z))\)
In this expression, the umber \(n\) of iteration has no need to be integer; sin cam be iterated even complex number of times.
References
- ↑
https://mizugadro.mydns.jp/PAPERS/2014susin.pdf
D.Kouznetsov. Super sin. Far East Jourmal of Mathematical Science, v.85, No.2, 2014, pages 219-238. - ↑
https://www.amazon.co.jp/-/en/Dmitrii-Kouznetsov/dp/6202672862
https://www.morebooks.de/shop-ui/shop/product/978-620-2-67286-3
https://mizugadro.mydns.jp/BOOK/468.pdf
D.Kouznetov. Superfunctions. Lambert Academic Publishing, 2020.
https://mizugadro.mydns.jp/PAPERS/2014susinL.pdf
https://www.pphmj.com/references/8246.htm
https://mizugadro.mydns.jp/PAPERS/2014susin.pdf
D.Kouznetsov. Super sin. Far East Journal of Mathematical Science, v.85, No.2, 2014, pages 219-238.
Keywords
«Abel function», «Abel equation», «Abelfunction», «Far East Journal of Mathematical Science», «Iterate», «sin», «SuSin», «Superfunction», «Superfunctions»,