Power function
Power function (Степенная функция) is one of the primary elementary functions;
(1) \(~ ~ ~ \mathrm{pow}_a(z) = z^a = \exp_z(a) = \exp(a \ln(z))\)
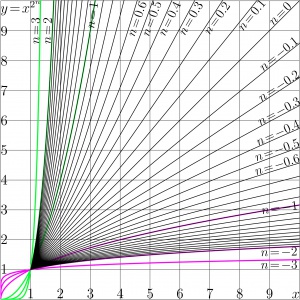
where \(a\) is parameter; often it is assumed that \(a\) is real. The real-real plot of function \(T(z)\!=\!z^a\) is shown in Fig.1 for several values of \(a\).
Generalisation
It is possible to consider a little bit more general case, let \(a\!=\!1\!+r\); and let
\(T(z)= \mathrm{Pow}_{c,r}(z)= c \, z^{1+r}\)
There are some reason to use new parameter \(r\!=\!a\! - \! 1\); formulas happen to be shorter.
For this case, the elementary superfunction \(F\) and the abelfunction \(G\) can be written as follows:
\(F(z)=c^{-1/r} \exp\big( (1\!+\!r)^z\, c^{1/r}\big)\)
\(G(z)=\displaystyle \frac{ \ln\big(c^{-1/r}\, \ln(c^{1/r}\,z\,) \big)}{\ln(1+r)}\)
These functions can be verified with the Mathematica code below:
F[z_] = Exp[c^(1/r)*(1+r)^z]/c^(1/r)
G[z_] = Log[Log[c^(1/r)*z]/c^(1/r)]/Log[1+r]
Simplify[F[1+G[z]], {r>0,c>0}]
The output is
\(\rm c\, z^{1+r}\)
That is just \(T(z)\)
In principe, the deduction below can be repeated with this generalised case. Historically, due to the bug in Mathematica software, case with \(c\!=\!1\) had been considered first; the Matehmatica did not want to simplify some expressions with previous notations:
FullSimplify[c^(1-p)^(-1) - c*(c^(1-p)^(-1))^p,{c>1,p>1}]
does
\(\rm c^{\frac{1}{1-p}}-c \left(c^{\frac{1}{1-p}}\right)^p\)
instead of expected 0
The change of variable, replacement of \(p\) to \(1+r\) leads to the expected result:
FullSimplify[ ReplaceAll[c^(1-p)^(-1) - c*(c^(1-p)^(-1))^p, p -> 1+r], {c>1,r>0}]
confirms, that the result should be 0 .
Special cases
The most used are the special cases for \(a\!=\!2\), called Quadratic function, and for \(a\!=\!3\), called Cubic function.
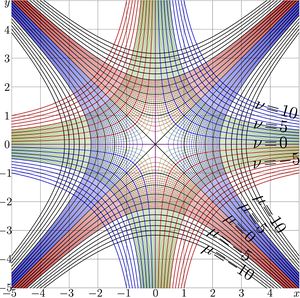
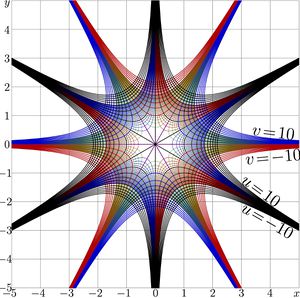
Complex map of the quadratic function (\(a\!=\!2\)) is shown in figure 2 at right with levels of constant real part and those of constant imaginary part, \(T(z)\!=\!z^2\); \(\mu \!+\!\mathrm i \nu=T(x\!+\!\mathrm i y)\).
Often, the constant coefficient is introduced in the right hand side of the definition of the power function; the resulting function is also qualified as power function. Such a generalisation is essential of the application in physics, while both argument and value of the power function are dimensional quantities.
Often, the additional coefficient is introduced in the definition of the power function, [1]:
\(T(z) = s z^p\)
The coefficient \(s\) is essential, if the power function approximates relation between two quantities that have different dimensions. In this article, the special case \(s\!=\!1\) is described.
Notations
In C++, \(~z^a=\mathrm{Pow}_a(z)~\) can be expressed as \(\rm pow(z,a)\). In some realizations, there may be some problems while one of arguments are integer and another one is complex. In some programming languages, including Mathematica, Maple, Matlab and in Latex (in the "math.mode"), the same can be written as z^a.
There is description of the Power function in the Russian version of Wikipedia [2].
Often, the function is considered with 2 parameters, including the leading coefficient into definition of function [1]. Here, for simplicity, the coefficient is assumed to be unity. For several real values \(a\), the graphic \(y=x^a\) is shown in figure 1.
In some cases of integer \(a\) the function has specific names.
For \(~a\!=\!3~\), the power function \(~z^a~\) is cubic function.
For \(~a\!=\!2~\), the power function \(~z^a~\) is quadratic function.
For \(~a\!=\!1~\), the power function \(~z^a\!=\!z~\), referring to the identity function.
For \(~a\!=\!0~\), the power function \(~z^a\!=\!1~\) refers to constant.
For \(~a\!=\!-1~\), the power function \(~z^a\!=\!1/z~\) and the power function is its own inverse function. For this case, often \(~f\!=\! f^{-1}~\) is called "inverse function" (without to indicate, for which function it is "inverse"); using such a term in a context, where the inversion of function take place, may cause confusions.
The confusion may appear also at the use of the superscript after the name of a function to indicate that after to evaluate the function, the power function should be applied to the result. Often this appears dealing with trigonometric functions, one writes, for example, \(\sin^a(z)\) instead of \(\sin(z)^a~\). In particular, at \(~a\!=\!-1~\), this writing may refer also to the ArcSin function. Such a confusion happens at the use of the Mathematica operation TeXForm: expressions \(f(z)^n\) are automatically replaced to \(f^n(x)\), mimicking the \(n\)th iteration of function \(f\). In TORI, the upper superscript after the function indicates its iteration.
Properties of the power function
the following expressions hold in the wide ranges of values of parameters \(a,b,z,p,q,n\):
\( (z)^n/z=z^{n-1}\)
\( (z^a)^b = z^{a+b}\)
\( (pa)^n=p^n q^n\)
However, the use for negative and comlex values of parameters may cause errors. For integer value of power \(n\), the expression \((a\!+\!b)^n\) can be expanded as follows
\( (a+b)^1=a+b\)
\( (a+b)^2=(a+b)(a+b)=a^2+2ab+b^2\)
\( (a+b)^3=(a+b)(a+b)(a+b)=a^3+3a^2b+3ab^2+b^3\)
and so on.
Derivative
The derivative of a power function can be derived from the properties of exp and ln:
\(\displaystyle {\mathrm{pow}_a}'(z)= \Big(\exp\big( a \ln(z) \big)\Big)^{\prime}_z=\exp\big( a \ln(z) \big) \,a/z=z^a a/z=a z^{a-1}\)
Such an expression is valid in wide range of parameters.
Integral
Form the expression for the derivative, the integration of the power function also can be derived:
\(\displaystyle \int_x^z t^a \mathrm{d}t = \frac{z^{a+1}}{a\!+\!1}- \frac{x^{a+1}}{a\!+\!1}\)
Such an expression is also valid in wide range of parameters, and, especially, while \(a\!\ne -1\).
Iterates of power function
The \(n\)th Iterate of power function can be expressed again through the power function in the following way:
(2) \( ~ ~ ~ {\mathrm {pow}_a}^n(z)=\mathrm{pow}_{b}(z)\)
with \(b=a^n\). This corresponds to the school–level rules
(3) \( ~ ~ ~ z^p z^q=z^{p+q}\)
(4) \( ~ ~ ~ ({z^p})^q=z^{pq}\)
however, such a rules should be used carefully, because for come complex values of \(p\), \(q\) and \(z\) the relations (3) and (4) are not valid. Since year 2005, the Mathematica software recognizes this and the Simplify and FullSimplify operations do not use substitutions (3) and (4) automatically before to get some additional information about values of the parameters involved.
The interesting property of iteration of the Power function is that
(5) \( \displaystyle ~ ~ ~ \mathrm{Pow}_{_{(a^n)}}(z) = (\mathrm{Pow}_a)^n(z)\)
For this reason, the expression
(7) \( ~ ~ ~ {\mathrm{Pow}_a}^n\)
can be interpreted in a way in the left hand side of (5), as well as the expression in the right hand side of (5), in wide range of values of parameters and the argument. (Assuming the same for other functions may lead to confusions.) For \(a\!=\!2\), the iterates of quadratic function are shown in Figure 2.
The power function is one of few functions, for which the iterates can be expressed in so simple way. For other function \(T\), the \(n\)th iterate \(T^n\) can be expressed through its superfunction \(~F~\) and the Abel function \(~G=F^{-1}~\),
(8) \(~ ~ ~ T^n(z)=F\Big(n+G(z)\Big)\)
However, for \(T=\mathrm{Pow_a}\), the expression (8) is also valid; examples for the corresponding superfunction \(~F~\) and the Abel function \(~G~\) are considered below.
Superpower
Superpower is superfunction for the transfer function \(T(z)\!=\!z^a\).
Superpower function is solution \(F\) of the transfer equation \(T(F(z))=F(z\!+\!1)\), that can be fwitten also as
\(F(z\!+\!1)=F(z)^a\).
For \(a\!>\!1\), the two real-holomorphic solutions can be written as
\(F(z)= \mathrm{SuPow}_a(z)=\exp(a^z)=\exp\!\Big(\exp\!\big(\ln(a)\,z\big)\Big)~\)
and
\(F(z)=\mathrm{SdPow}_a(z)=\exp(-a^z)\) \( =\exp\!\Big(\!-\exp\!\big(\ln(a)\,z\big)\Big)\) \(\displaystyle =\frac{1}{\mathrm{SuPow}_a(z)}\) \( = \mathrm{SuPow}_a\!\big(z + \mathrm i \pi/\ln(a )\big) \)
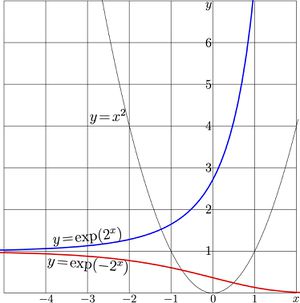
For \(a\!=\!2\), the explicit plots of these two functions are shown in Fig.3.
Complex map of function \(\mathrm{SuPow}_2\) is shown in Fig.4 with lines of constant real part \(u\) and lines of constant imaginary part \(v\);
\(u\!+\!\mathrm i v \!=\! \mathrm{SuPow}_2(x\!+\!\mathrm i y)\)
For real values of argument function \(\mathrm{SuPow}_2\) approaches its limiting value unity at \(-\infty\) and shows the double-exponential growth at \(+\infty\); this growth is seen in both Fig.3 and FIg.4.
Functions \(\mathrm{SuPow}_a\) and \(\mathrm{SdPow}_a\) are periodic; the period is
\(P= \mathrm i 2 \pi/\ln(a )\)
For positive \(a\), the period is pure imaginary. At \(a\!=\!2\), for the case shown in figure 4, the period
\(P=\mathrm i 2\pi / \ln(2) \approx 9.06472028365\)
The map in Fig.4 is reproduced at the translations for, roughly, \(~\pm 9.06472028365 ~\) along the Imaginary axis. The range of FIg.4 covers a little bit more that one period of the function.
Functions \(\mathrm{SuPow}_a\) and \(\mathrm{SdPow}_a\) can be expressed through each other,
\(\mathrm{SdPow}_a(z)=\mathrm{SuPow}_a\big(z\!+\mathrm i \pi/\ln(a ) \big)\)
In particular, map of function \(\mathrm{SdPow}_2\) appear as displacement of map of \(\mathrm{SdPow}_2\), shown in Fig.4, for \(P/2\), id est, as translation for, roughly, 4.53236014183 along the imaginary axis.
More detailed descriptions of superfunctions of the power function should be loaded in articles Superpower, SuPow, SdPow.
Abelpower
For superpower function \(F\), the inverse function \(G\!=\!F^{-1}\) is solution of the Abel equation,
\(G(T(z))=G(z)+1\)
The two expect realisations (corresponding to the two superfunctions \(F\) above) are:
\(G(z)=\mathrm{AuPow}_a(z)\) \( =\log_a\!\big(\ln(z)\big)\) \( =\ln\!\big(\ln(z)\big)/\ln(a)\) \( =\ln^2(z)/\ln(a) \)
and
\(G(z)=\mathrm{AdPow}_a(z)\) \( =\log_a\!\big(\ln(1/z)\big)\) \( =\ln\!\big(\ln(1/z)\big)/\ln(a)\) \( =\ln^2(1/z)/\ln(a)\)
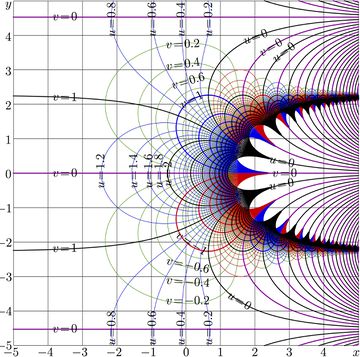
for \(a\!=\!2\), the complex map of the first of them is shown in figure at right with levels of constant real part and levels of constant imaginary part;
\(u\!+\!\mathrm i v=\mathrm{AuPow}_2(z)(x\!+\!\mathrm i y)\)
Use of the power function
Power function has many applications during past centuries. Initially, the power function could be used for short writing of expressions with polynomials with numbers. However, after discovery of exponential and logarithm, by default, \(~z^a~\) is interpreted as \(~\exp\!\big(\ln(a)\,z\big)~\).
With such an interpretation the power function can be applies not only to numbers, but also to elements other sets, where operations \(\exp\) and \(\ln\) are already defined. Even if some of these operations are not yet defined, \(z^n\) for natural number \(n\) can be considered as just iteration of function "multiplication to \(z\)" applied to unity \(z\) times. In particular, in such a way the power function is interpreted in quantum mechanics; for example, \(\hat p^n \psi\) refers to iterative application of operator \(\hat p\) to the state \(\psi\).
In TORI, the power function and its iterates are applied to the complex numbers, but the application to the operators of quantum mechanics is expected in future.
Power function is used as simple example of the Transfer function, for which the Superfunction and the Abel function can be written as elementary functions. This helps to trade the use of methods, developed for other transfer functions (for which the superfunction is not elementary).
The superpower function can be constructed with regular iteration. For transfer function \(T(z)=z^p\), the primary approximation of superfunction \(F\) appears as
\(\displaystyle F_M(z)=1+\sum_{n=1}^{M} a_n \exp(kz)^n\)
where \(M>1\) is constant integer, and increment \(k=\ln( p)\).
Coefficients \(a\) of the regular iteration appear at substitution \(F\rightarrow F_M\) in the transfer equation
\(F(z+1)=T(F(z))\)
and the asymptotic analysis. For \(a_1\!=\!1\), these coefficients can be calculated with the mathematica code below:
T[z_] = z^p
m = 1;
f[m, x_] = 1 + x
f1[m, x_] = 1 + p*x
m = 2;
f[m, x_] = f[m - 1, x] + a[m] x^m
f1[m, x_] = f1[m - 1, x] + a[m] p^m x^m
q[m] = Coefficient[Series[f1[m, x] - T[f[m, x]], {x, 0, m}], x^m]
su[m] = Extract[Solve[q[m] == 0, a[m]], 1]
m = 3;
f[m, x_] = ReplaceAll[f[m - 1, x], su[m - 1]] + a[m] x^m
f1[m, x_] = ReplaceAll[f1[m - 1, x], su[m - 1]] + a[m] p^m x^m
q[m] = Coefficient[Series[f1[m, x] - T[f[m, x]], {x, 0, m}], x^m]
su[m] = Extract[Solve[q[m] == 0, a[m]], 1]
(* and so on for m=4, m-5, ..)
This code confirms, that the primary expansion is just truncated series go expansion of exponent in the exact superfunction SuPow
\(F(z)=\exp( \exp(kx))\)
Similar verification can be done for superfunction SdPow with \(a_1\!=\!-1\).
References
Keywords
Abel function, AdPow, AuPow, Elementary function, SdPow, SuPow, Superfunctions, Superpower,, Elementary function,,,