AdPow
AdPow is specific Abelpower function, id est, the specific Abel function for the Power function.
AdPow can be expressed as elementary function,
\(\mathrm{AdPow}_a(z)=\log_a(\ln(1/z))\)
Where \(a\) is parameter. Usually, it is assumed that \(a\!>\!0\).
AdPow is inverse function of SdPow, that, in its turn, is superfunction of the power function.
AdPow and AuPow
Another abelfunction for the power function is called AuPow;
\(\mathrm{AdPow}_a(z)=\log_a(\ln(z))\)
AdPow is related with AuPow function with simple relation:
\(\mathrm{AdPow}_a(z)=\mathrm{AuPow}_a(1/z)\)
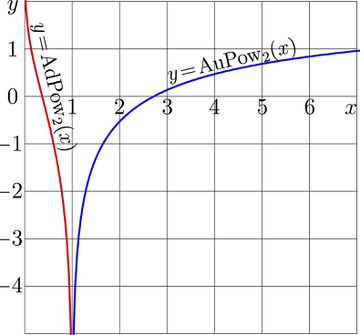
For \(a\!=\!2\), both functions AdPow and AuPow are shown in Fig.1
For the same \(a\!=\!2\), complex map of function AdPow is shown in Fig.2.
Inverse function
For AdPow, the inverse function is SdPow, that is superpower function, id est, superfunction of the power function:
\(\mathrm{AdPow}_a=\mathrm{SdPow}_a^{-1}\)
SdPow satisfies the Transfer equation
\(\mathrm{SdPow}_a(z\!+\!1)=\mathrm{SdPow}_a(z)^a\)
SdPow is elementary function,
\(\mathrm{SdPow}_a(z)= \exp(-a^z)\)
Applications
AdPow appears as example of the Abel function that can be expressed as elementary function. This allows to trace evaluation of superfunction through the regular iteration; the fixed point unity can be used for the calculation.
References
Keywords
Abel function AdPow Abel function Elementary function Power function SdPow Superfunctions SdPow Superfunctions