Abelpower
Abelpower appears inverse function of the superpower function.
Abelpower is Abel function for the power function, id est, transfer function \(T(z)\!=\!z^a\) where \(a\) is parameter. Usually, it is assumed, that \(a\!>\!1\).
Superpower and Abelpower
For the transfer function \(T(z)\!=\!z^a\), the two superfunctions
\(F(z)=\exp(a^z)\)
and
\(F(z)=\exp(-a^z)\)
are denoted as SuPow and SdPow. For superpower function \(F\), the inverse function \(G\!=\!F^{-1}\) is solution of the Abel equation,
\(G(T(z))=G(z)+1\)
The two solutions (corresponding to the two superfunctions \(F\) above) are:
\(G(z)=\mathrm{AuPow}_a^{-1}(z)=\mathrm{AuPow}_a(z)\) \( =\log_a\!\big(\ln(z)\big)\) \( =\ln\!\big(\ln(z)\big)/\ln(a)\) \( =\ln^2(z)/\ln(a) \)
and
\(G(z)=\mathrm{AdPow}_a^{-1}(z)=\mathrm{AdPow}_a(z)\) \( =\log_a\!\big(\ln(1/z)\big)\) \( =\ln\!\big(\ln(1/z)\big)/\ln(a)\) \( =\ln^2(1/z)/\ln(a)\)
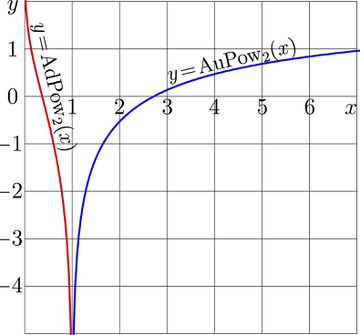
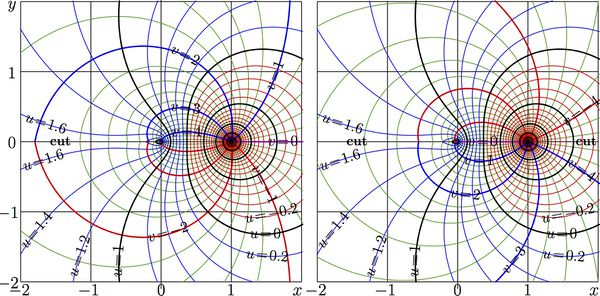
These functions are called Abelpower functions. For \(a\!=\!2\), the explicit plots of these two functions are shown in figure at top. The complex maps of them are shown below with levels of constant real part and levels of constant imaginary part;
\(u\!+\!\mathrm i v=G(x\!+\!\mathrm i y)\)
In the most of the complex plane, values of functions AuPow\(_a\) and AdPow\(_a\) differ for a constant; however, they have different cut lines. In order to compare the systems of cuts for these two functions, the zooming of the central parts of maps for AuPow\(_2\) and AdPow\(_2\) are shown together in figure
Application
Abelpower function shows behaviour, similar to those for other abelfunctions, (see Table of superfunctions), that cannot be expressed as elementary functions.
So, the primary application of the superpower and abelpower functions is testing, tracing of general algorithms for evaluation of superfunctions and abelfunctions. Superpower and abelpower are easy to evaluate through their explicit representations; so, the precision of some general method of evaluation is easy to estimate.
Articles about Abelpower function are loaded in TORI as draft of for the special chapter of the Book Superfunctions. Such a chapter is expected to be especially useful for the colleagues who complain that "The formalism of superfunctions is too complicated"
References
Keywords
Abel function, AdPow, AuPow, Power function, Superfunction, Superfunctions, SdPow, SuPow,