SuPow
SuPow is specific superpower function, id est, the superfunction of the power function \(~z\mapsto z^a\!=\!\exp(\ln(z) \,a)~\)
For given parameter \(a\),
\(\mathrm{SuPow}_a(z)=\exp(a^z)\)
Usually, it is assumed, that \(a\!>\!1\).
Transfer function
Function \(F\!=\!\mathrm{SuPow}_a\) is superfunction for the specific power function \(T(z)\!=\!z^a\). The superfunction satisfies the transfer equation
\(T(F(z))=F(z\!+\!1)\)
another solution is denoted as SdPow;
\(\mathrm{SdPow}_a(z)=\exp(-a^z)\)
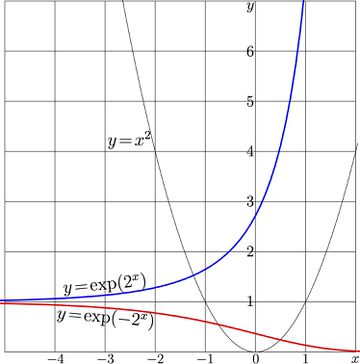
For \(a\!=\!2\) graphics \(y=T(x)\), \(y=\mathrm{SuPow}_2(x)\) and \(y=\mathrm{SdPow}_2(x)\) are shown in Fig.1.
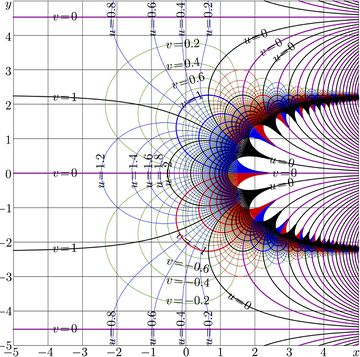
For \(a\!=\!2\), complex map of function \(\mathrm{SuPow}_a\) is shown in Fig.2.
SuPow and SdPow
Function \(\mathrm{SuPow}_a\) is periodic, as well as function \(\mathrm{SdPow}_a\)
The period \(P=2\pi\mathrm i / \ln(a)\) is the same for both these functions.
For \(a\!>\!1\), the period is pure imaginary. A little bit more than one period fits the range of map in Fig.2.
Such a periodicity is typical for a superfunction of a transfer function with a real fixed point. Some of thiese function are listed in the Table of superfunctions.
Functions SuPow and SdPow are related with expression
\(\mathrm{SuPow}_a(z)=\mathrm{SdPow}_a(z\!+\!P/2)\)
Similar relations hold also for many other pairs of periodic superfunctions of some transfer function with two fixed points
However, namely the superpower functions have also the specific relation,
\(\displaystyle \mathrm{SuPow}_a(z)=\frac{1}{\mathrm{SdPow}_a(z)}\)
Inverse function
The inverse function AuPow\(=\mathrm{SuPow}^{-1}\) is also elementary function;
\(\mathrm{AuPow}_a(z)=\log_a(\ln(z))\)
AuPow is the Abel function for the same transfer function \(T(z)=z^a\) and satisfies the Abel equation
\(\mathrm{AuPow}_a(z^a)=\mathrm{AuPow}_a(z)+1\)
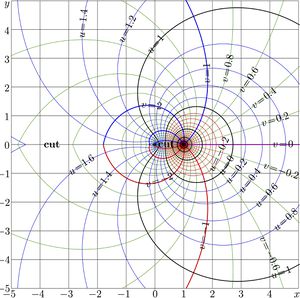
Complex map of function \(\mathrm{AuPow}_2\) is shown in figure at right.
For \(a\!>\!1\), function \(\mathrm{AuPow}_2\) has cut line along the real axis from \(1\) to \(-\infty\).
Application
References
Keywords
AuPow, Book, Power function, SdPow, Superfunction, Superfunctions, Superpower