SuperFactorial
In TORI, SuperFactorial, or "superfactorial", SuFac is superfunction of factorial constructed at its fixed point 2.
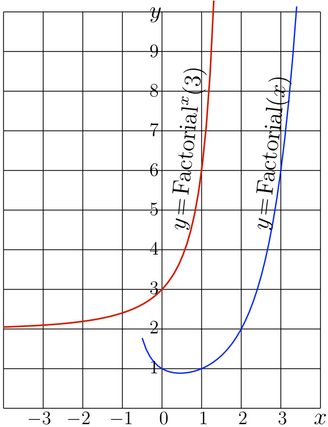
The smallest integer larger than 2 (id est 3) is chosen as its value at zero, \(\mathrm{SuperFactorial}(0)=3~\). Then,
\(\mathrm{SuperFactorial}(1)\) \(=\) \(3!\) \(=\) \(6\),
\(\mathrm{SuperFactorial}(2)=6!=720\),
\(\mathrm{SuperFactorial}(3)=720!~\) and so on;
- \(\mathrm{SuperFactorial}(z)=\mathrm{Factorial}^z(3)\)
Here, the upper index of a function indicates the number of iterations.
Superfactorial satisfies the transfer equation
- \(\mathrm{Factorial}(\mathrm{SuperFactorial}(z))=\mathrm{SuperFactorial}(z\!+\!1)\)
SuperFactorial [1] should not be confused with hyperfactorial [2], expressed with
- \(\displaystyle \mathrm{Hyperfactorial}(n)=\prod_{k=1}^{n}k^k\)
for integer values of the argument and with relatively simple integral for the complex values.
Nest
Superfactorial can be expressed through the Mathematica built-in function Nest,
- \(\mathrm{SuperFactorial}[z]=\mathrm{Nest}[\mathrm{Factorial}, 3, z]\)
For \(z\in \mathbb N\), such an expression is recognized correctly. [3]
\(\mathrm{SuperFactorial}(z)\) is just \(z\)th iteration of Fatorial, evaluated at 3; so,
- \(\mathrm{SuperFactorial}(0)=3\)
- \(\mathrm{SuperFactorial}(1)=\mathrm{Factorial}(\mathrm{SuperFactorial}(0))=\mathrm{Factorial}(3)=6\)
- \(\mathrm{SuperFactorial}(2)=\mathrm{Factorial}^2(3)=\mathrm{Factorial} \big( \mathrm{Factorial}(3)\big)=\mathrm{Factorial}(6)=6!=720\)
- \(\mathrm{SuperFactorial}(3)=\mathrm{Factorial}^3(3)=\mathrm{Factorial}(720)=720!\)
- \(\mathrm{SuperFactorial}(4)=\mathrm{Factorial}^4(3)=\mathrm{Factorial}(720!) ~\)
and so on; however, the factorial of 720 is already too big and cannot be shown here as integer constant. Along the real axis, the SuperFactorial grows up faster than tetration does.
Up to year 2024, the Mathematica function Nest is implemented only for positive integer values of the number of the last argument. Attempts to use it in other ways causes the error messages.
History
First, the superfunction of factorial is described in 2010 in the Moscow University Physics Bulletin [1]. That publication defined the \(\sqrt{!\,}\) as holomorphic function, giving sense to the logo of the Physics Department of that University. As a by-product, the SuperFunction of Factorial and that for some other special functions are considered there. Below, one of superfunctions of factorial is called SuperFactorial. The more detailed historic overview is presented in the article Square root of factorial.
Regular iteration
The straightforward application of the regular iteration to the solution \(F\) of the transfer equation
- \( (1)~ ~ ~ ~ ~ F(z\!+\!1) = \mathrm{Factorial}(F(z))\)
is described below.
Aiming to build–up the growing function, the biggest among the real fixed points of factorial should be chosen as value at \(-\infty\), so, search the solution in the following form:
- \((2)~ ~ ~ ~ ~ F(z)=2+ a_1 \varepsilon + a_2 \varepsilon^2 +..\)
where
- \((3)~ ~ ~ ~ ~ \varepsilon=\exp(kz)\)
It is convenient to set \(a_1=1~\). Then other coefficients \(a\) and constant \(k\) can be determined substituting such a representation into the transfer equation (1):
- \((4) ~ ~ ~ ~ ~ \mathrm{Factoral}(2+ \varepsilon + a_2 \varepsilon^2 +..) - (2+ K \varepsilon + K^2 a_2 \varepsilon^2 +..)=0\)
where \(K=\exp(k)\). The expansion of the left hand side of equation (1) into the power series with respect to \(\varepsilon\) and equalizing to zero the coefficients gives the equation for \(K\) and those for \(a_2\), \(a_3\), .. For example,
- \(\mathrm{Factorial}'(2)-K=0\)
- \(\mathrm{Factorial}'(2) a_2+\mathrm{Factorial}''(2)\frac{1}{2} a_1^2-K^2 a_2=0\)
The derivatives of Factorial are known, in particular,
- \(\mathrm{Factorial}'(2)=3-2 \gamma\),
- \(\mathrm{Factorial}''(2)= 2 - 6 \gamma + 2 \gamma^2 + \pi^2/3\)
where \(\gamma=-\mathrm{Factorial}'(0) \approx -0.5772156649015329\) is the Euler constant. Then,
- \(K=3-2\gamma~\) ; \(~ ~ ~k=\ln(K)=\ln(3-2\!~\gamma) \approx 0.6127874523307\)
- \(a_2=\frac{\pi^2+6\gamma^{2}-18\gamma+6}{12(3-5\gamma+2\gamma^{2})} \approx 0.79873183517243454\)
and similar expressions for higher coefficients \(a\).
The series (2) diverges, but the equation (1) allow to transfer the approximation from the range where it is valid (sufficient values of \(-\Re(z)\) to other values and therefore get the required precision of evaluation of \(F\).
In order to satisfy condition SuperFactorial(0)=3, it is sufficient to set
- \(\mathrm{SuperFactorial}(z)=F(x_0\!+\!z)\)
where \(~x_0\!\approx\! -0.91938596545217788~\) is solution of equation \(~F(x_0)\!=\!3~\).
Properties of Superfactorial
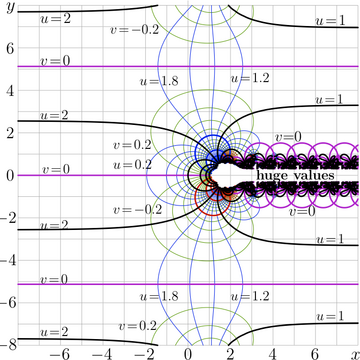
The complex map of SuperFactorial is shown at the figure 2. The contour plots of
\( u\!=\!\Re(\mathrm {SuperFactorial} (x\!+\!\mathrm i y)\) and
\( v\!=\!\Im(\mathrm {SuperFactorial} (x\!+\!\mathrm i y)\)
intersect on the right angles, as they are supposed to do at the complex map of any holomorphic function.
The integer values of \(u\) or \(v\) are marked with thick lines; thin lines correspond to the intermediate levels.
SuperFactorial is real-holomorphic, at lest in the range \(\{z \in \mathbb C : \Re(z)\le 2\}\).
SuperFactorial is periodic function; the period
\(P = \frac{2 \pi \mathrm i}{k} \approx 10.2534496811560279265772640691397~\mathrm i\)
At non-negative integer values of the argument, SuperFactorial takes integer values; in particular, \(\mathrm{SuperFactorial}(0)=3~\)
Function \(\tilde F(z)=\mathrm{SuperFactorial}\left(z+\frac{T}{2}\right)\) is also real-holomorphic; it smoothly decreases from value 2 at \(-\infty\) to unity at \(+\infty\) along the real axis. Such a complementary superfunction typically exists at the consruction of a superfunction with regular iteration at a real fixed point.
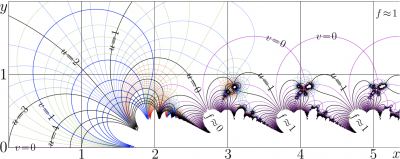
Singularities
SuperFactorial is not entire function, over-vice, it would have negative integer values somewhere, which is not consistent with the transfer equation (1): Factorial at negative integers has poles. The unity translation form any point, where the SuperFactorial has negative integer value leads to a singularity.
The conclusion about the singularities is confirmed by the zoom-in from the comlpex map of the SuperFactorial. The figure indicates that the singularities of SuperFactorial are located within half-strips
- \( z\in \mathbb C :\) \( \{ \Re(z) >\!2.7 ~,~ |\Im(z)\!+\!T n|<1 ~\mathrm{for~ some~} n\in \mathbb Z \}\)
Outside these half-strips, the SuperFactorial exponentially approaches 2 as the real part of the argument goes to \(-\!\infty\) and approaches unity as the real part of the argument goes to \(+\!\infty\).
AbelFactorial
The inverse function of SuperFactorial is AbelFactorial; at least in some vicinity of the half-line along the real axis, the relations
- \(\mathrm{SuperFactorial}( \mathrm{AbelFactorial}(z))=z\)
- \(\mathrm{AbelFactorial}( \mathrm{SuperFactorial}(z))=z\)
The AbelFactorial satisfies the Abel equation
- \(\mathrm{Abelfactorial}( \mathrm{Factorial}(z))= \mathrm{AbelFactorial}(z)+1\)
See the special article AbelFactorial for the details.
Together, the AbelFactorial and the SuperFactorial allow to express (and to evaluate) the iterations of Factorial in the following way:
- \(\mathrm{Factorial}^c(z)=\mathrm{SuperFactorial}\big(c + \mathrm{AbelFactorial}(z)\big)\)
where number \(c\) of iterations has no need to be integer; it can be even complex, and for some domain of \(c,d,z\in C^3 \subseteq \mathbb C^3\), the relation
- \(\mathrm{Factorial}^c\big(\mathrm{Factorial}^d(z)\big)=\mathrm{Factorial}^{c+d}((z)\)
as if takes place for the exponentiation. This justifies the notation square root of factorial for the half–iteration of Factorial, id est
- \(\sqrt{!~}~=~\mathrm{Factorial}^{1/2}\)
In wide domain of values of \(z\), the relation
- \(\sqrt{!~}~(\sqrt{!~}(z))~=~\mathrm{Factorial}(z)=z!\)
See the special article «Square root of factorial» for the details.
Existence and uniqueness
The existence and uniquness of a SuperFunction for a holomorphic fixed point is considered in [4]. The regular iteration gives the explicit proof of existence, while the requirements on the behavior at zero and the asymptotic properties provide the uniqueness. However, there are many other fixed points, and each of them can be used to construct a superfunction of factorial, pretty different from the SuperFactorial described above.
The new superfunctions of Factorial can be constructed with periodic perturbation of its argument, let
- \(f(z)=\mathrm{SuperFactorial}(z+\zeta(z))\)
where \(\zeta\) is some hoomorphic function, periodic with period unity. Function \(f\) satisfies the same transfer equation {1} as the SuperFactorial; however, the periodicity or \(\zeta\) does not allow it to decay as the real part of the argument goes \(-\infty\); as the result, neither the asymptotic behavior (2) of the SuperFactorial, nor its periodicity with period \(T\) can be achieved. In this sense, with specification of the asymptotic behavior and the periodicity, the SuperFactorial is unique.
The SuperFactorial above seems to be the simplest among various SuperFunctions of Factorial, if one exclude functions that are identically equal to a constant. Other non-trivial superfunctions of Factorial show complicated behavior: and even the holomorphism in the left hand side of the complex plane cannot be achieved. Up to year 2011, a statement has status of conjecture, and the rigorous proof may be matter for the good outstanding research.
Algorithmic implementation of Superfactorial
C++ implementation
For the efficient evaluation of SuperFactorial, the regular iteration is suitable; the reasonable number of terms in the partial sum is of order of dozen. Then, within few tens of operations, one can get of order of 15 decimal digits, that is sufficient for the complex double implementation. The C++ code for the evaluation of SuperFactorial used to generate the figures is expected to be loaded, as a common component of the generators of the figures.
In the final version, the SuperFactorial is expected to be implemented as
- complex<double> SuperFactorial(complex<double> z)
and its inverse function is expected to be implemented as
- complex<double> AbelFactorial(complex<double> z)
The preliminary versions of the routines can be uploaded upon request; the final version will appear after to check the compatibility with other codes that are already loaded in TORI and in the Citizendium.
Mathematica implementation
In version of 2011, Mathematica already has name reserved for the iteration of functions, namely, Nest. The call of such a function may have form
- Nest[f,a,z]
where \(f\) indicates the name of the function, \(z\) is number of iterations, and \(a\) is initial value.
Then, \(\mathrm{SuperFactorial}(z)\) can be expressed with
- Nest[Factorial,3,z]
and the \(c\)th iteration of Factorial, id est, \(\mathrm{Factorial}^c(z)\) could be written as
- Nest[Factorial,z,c]
In the current version of Mathematica (year 2011), the Nest is implemented only for the case, when the last argument can be simplified to an constant , expressed with a natural number. [5]
The upgrade of the implementation of Nest may include the table of SuperFunctions and corresponding Abel functions, their properties and ways of the efficient evaluation with required precision.
Confusion
Term SuperFactorial should not be confused with Superfactorial [6][7], that denotes function \[ g(n)= n\$ = ^{(n!)}\!(n!)=\underbrace{n!^{n!^{n!}..}}_{n!} \] Which means the factorial of \(n\) itetrated to itself or equivalently the factorial of \(n\) pentated to 2.
No any complex map of the "superfactorial" defined in such a way is supplied at [7], nor application is suggested, nor comparison with fastly growing Ackermann functions is supplied - in contrast with the \(\sqrt{\ !\ } \) for the SuperFactorial and AbelFactorial interpreted in the TORI notations.
In this sense, the First of the TORI axioms for the case of Googology causes doubts.
Before such an application is suggested, the Superfactorial in sense of [6][7] is not considered in TORI.
Conclusions
From the point of view of construction of superfunctions, there is nothing specific in the Factorial: the SuperFactorial is constructed in the same way as superfunction for \(\exp_b\) for \(1<b<\exp(1/\mathrm e)\), described in [4] or that for the logistic operator [8].
SupeFactorial, together with its inverse function (id est, AbelFactorial) allows to define the \(n\)th iterate of factorial for non-integer values of \(n\); in particular, the square root of factorial (that was believed to have no sense
[9][10]) appears as half-iteration of factorial.
This symbol of this function, id est, \(\sqrt{!\,}\) is used as central part of logo of TORI in years 2009-2018. Then, during unfolding of the Putin world war, any allusion with Russia and with any Moscovian organization (even the University) becomes toxic; so, the LOGO had been changed to four simple formulas related to Square root of exponential.)
References
- ↑ 1.0 1.1 http://www.ils.uec.ac.jp/~dima/PAPERS/2009supefae.pdf D.Kouznetsov, H.Trappmann. Superfunctions and square root of factorial. Moscow University Physics Bulletin, 2010, v.65, No.1, p.6-12.
- ↑ http://mathworld.wolfram.com/Hyperfactorial.html
- ↑ However, in the current (for year 2011) implementation of Nest function in the Mathematica software allows to evaluate the SuperFactorial only for very few values of the argument; in the most of cases, the attempt to use the Nest function for evaluation of SuperFactorial causes the only diagnostic message and cannot be used to plot the SuperFactorial.
- ↑ 4.0 4.1 http://www.ams.org/journals/mcom/2010-79-271/S0025-5718-10-02342-2/home.html D.Kouznetsov, H.Trappmann. Portrait of the four regular super-exponentials to base sqrt(2). Mathematics of Computation, 2010, v.79, p.1727-1756.
- ↑ http://reference.wolfram.com/mathematica/ref/Nest.html BUILT-IN MATHEMATICA SYMBOL Tutorials. Nest.
- ↑ 6.0 6.1 https://mathworld.wolfram.com/Superfactorial.html The Superfactorial of n is defined by Pickover (1995) as // n$=n!^(n!^(·^(·^(·^(n!)))))_()_(n!). (1) // The first two values are 1 and 4, but subsequently grow so rapidly that 3$ already has a huge number of digits. ..
- ↑ 7.0 7.1 7.2 https://googology.fandom.com/wiki/Talk:Superfactorial .. The Kouznetsov superfactorial is another kind of superfactorial. Should it be included? ..
- ↑ http://www.springerlink.com/content/u712vtp4122544x4 D.Kouznetsov. Holomorphic extension of the logistic sequence. Moscow University Physics Bulletin, 2010, No.2, p.91-98.
- ↑ https://www.phys.msu.ru/rus/about/sovphys/ISSUES-2007/5(58)-2007/58-5/ V.P.Kandidov. About the time and myself. 1987.05.18. (In Russian) .. О ВРЕМЕНИ И ФАКУЛЬТЕТЕ, О КАФЕДРЕ И О СЕБЕ. 70-тилетие профессора В.П.Кандидова. .. « По итогам студенческого голосования победителями оказались значок с изображением рычага, поднимающего Землю, и нынешний с хорошо известной эмблемой в виде корня из факториала, вписанными в букву Ф. Этот значок, созданный студентом кафедры биофизики А.Сарвазяном, привлекал своей простотой и выразительностью. Тогда эмблема этого значка подверглась жесткой критике со стороны руководства факультета, поскольку она не имеет физического смысла, математически абсурдна и идеологически бессодержательна. ..»
- ↑ https://www.nkj.ru/archive/articles/1023/ 250 anniversary of the Moscow State University. (In Russian) ПЕРВОМУ УНИВЕРСИТЕТУ СТРАНЫ - 250! Наука и жизнь, 2005, N1 «На значке физфака в букву "Ф" вписано стилизованное изображение корня из факториала (√!) - выражение, математического смысла не имеющее.»
Keywords
«AbelFactorialR.png», «ArcCosc», «Complex map», «FacIteT.jpg», «Factorial», «IterfacPlotT.png», «Iteration», «Mathematica», «Moscow University Physics Bulletin», «Name of function», «Pentation», «QFacMapT.png», «QFactorialQexp.jpg», «Regular Iteration», «Sfaczoo300.png», «Special function», «SuFac», «SuperFactorial.cin», «Superfactorial.cin», «Superfactorial (That caused fonfusions)», «Superfunction», «Superfunctions», «Square root of factorial», «Square root of exponential», «SuZex», «SuZex approximation», «SuperFacMapT.png», «SuperFacPlotT.png», «Superfactocomple1.png», «Superfactorea500.png», «SuperFacZoomT.png», «Superfac.cin», «Superfunctions», «Table of superfunctions»,