Square root of exponential
Square root of exponential \(\varphi=\sqrt{\exp}=\exp^{1/2}\) is half-iteration of the exponential, id est, such function that its second iteration gives the exponential:
- \( (1) ~ ~ ~ \varphi(\varphi(z))=z\)
Such a \(\varphi\) is assumed to be holomorphic function for some domain of values of \(z\).
Explicit plot \(y=\varphi(x)=\exp^{1/2}(x)\) is shown with thick blue curve in figure at right.
For comparison, other iterates of exponential, id est, \(y=\exp^{n}(x)\) are shown with thin lines.
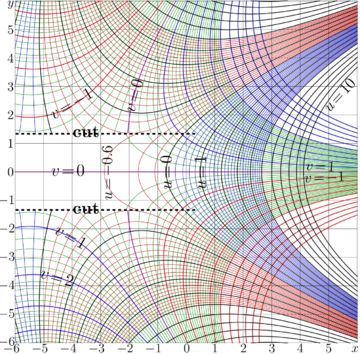
Complex map of function \(\varphi\) is shown in figure below.
Function \(\sqrt{\exp}\) should not be confused with \(z\mapsto \exp(z)^{1/2}\); in the range of holomorphism, the last can be reduced to \(\exp(z/2)\).
History
There exist many solutions of equation (1). Some of them are considered in y.1950 by Helmuth Kneser [1] in the middle or 20 century. But the real-holomorphic solution was not constructed that time.
In the beginning of century 21, the real-holomorphic solution \(\varphi\) has been suggested [2] in terms of tetration \(\mathrm{tet}\) and ArcTetration \(\mathrm{ate}\),
- \( (2) ~ ~ ~ \displaystyle \varphi(z)=\sqrt{\exp}(z) = \exp^{1/2}(z)=\mathrm{tet}\Big(\frac{1}{2}+\mathrm{ate}(z)\Big)\)
and namely this function is considered as default square foot of exponential. Expression (2) is just special case of the general expression of the \(c\)th iteration of some transfer function \(T\) through its superfunction \(F\) and the corresponding Abel function \(G=F^{-1}\):
- \((3) ~ ~ ~ \displaystyle T^c(z)=F(c+G(z))\)
In the equation (3), the number \(c\) of iteration can no need to be integer; it can be fractional, irrational or even complex. However, \(T^c(z)\) should not be confused with \(T(z)^c\). Equation (2) comes from (3) at \(T\!=\!\exp\), \(F\!=\!\mathrm{tet}\) and \(G\!=\!\mathrm{ate}\).
The square root of exponential seems to be the first non-trivial function for which the non-trivial non-integer iterations were reported, a "Holy Graal cup" [3] that opened the research of various superfunctions. In the similar way, the half-iteration of the logistic sequence [4] is constructed in terms of the superfunction and the Abel function, and similarly, the square root of factorial [5] can be expressed in therms of the SuperFactorial and AbelFactorial (or "ArcSuperFactorial") functions.
Uniqueness
The additional conditions on the behavior of the ArcTetration in vicinity of the fixed points of the logrithm provide the uniqueness of the ArcTetration [6], and, therefore, the uniqueness of the suggested real-holomorphic square root of the exponential.
Generalization
Equation (2) defines the square root of exponential as the \(\frac{1}{2}\)th iteration of the exponentis. It is special case of equation (3).
The similar expression for the evaluation of the half-iteration can be used also for the exponentials to various values of base, \(\exp_b\) for \(b\!>\!1\), as soon as the corresponding tetration and arctetration are implemented [7][8][9].
Square root of various functions can be interpreted as a halfiteration. However, the writing \(T^c(z)\) should not be confused with \(T(z)^c\), nor with \(T(z^c)\); these are pretty different expressions.
Keywords
«Abel equation», «Abel function», «ArcTetration», «Exponential», «Superfunction», «Table of superfunctions», «Tetration», «Transfer equation», «Transfer function»,
References
- ↑ http://www.digizeitschriften.de/dms/img/?PPN=GDZPPN002175851 H.Kneser. Reelle analytische Lösungen der Gleichung \(\varphi(\varphi(x))=e^x\). Equationes Mathematicae, Journal fur die reine und angewandte Mathematik 187 56–67 (1950)
- ↑ http://www.ils.uec.ac.jp/~dima/PAPERS/2009analuxpRepri.pdf D.Kouznetsov. Analytic solution of F(z+1)=exp(F(z)) in complex z-plane. Mathematics of Computation, v.78 (2009), 1647-1670.
- ↑ http://en.wikipedia.org/wiki/Holy_Grail
- ↑ http://www.springerlink.com/content/u712vtp4122544x4/ D.Kouznetsov. Holomorphic extension of the logistic sequence. Moscow University Physics Bulletin, 2010, No.2, p.91-98.
- ↑ http://www.ils.uec.ac.jp/~dima/PAPERS/2009supefae.pdf D.Kouznetsov, H.Trappmann. Superfunctions and square root of factorial. Moscow University Physics Bulletin, 2010, v.65, No.1, p.6-12.
- ↑ http://www.springerlink.com/content/u7327836m2850246/ H.Trappmann, D.Kouznetsov. Uniqueness of Analytic Abel Functions in Absence of a Real Fixed Point. Aequationes Mathematicae, 81, p.65-76 (2011)
- ↑ http://www.ils.uec.ac.jp/~dima/PAPERS/2010vladie.pdf D.Kouznetsov. Superexponential as special function. Vladikavkaz Mathematical Journal, 2010, v.12, issue 2, p.31-45.
- ↑ http://www.ams.org/journals/mcom/2010-79-271/S0025-5718-10-02342-2/home.html D.Kouznetsov, H.Trappmann. Portrait of the four regular super-exponentials to base sqrt(2). Mathematics of Computation, 2010, v.79, p.1727-1756.
- ↑ http://www.ils.uec.ac.jp/~dima/PAPERS/2011e1e.pdf H.Trappmann, D.Kouznetsov. Computation of the Two Regular Super-Exponentials to base exp(1/e). Mathematics of Computation, in press, 2011.
Keywords
«Abel function», «ArcTetration», «Hellmuth Kneser», «Square root of exponential», «Square root of factorial», «Superexponential», «SuperFactorial», «Superfunction», «Superfunctions», «Tetration»,