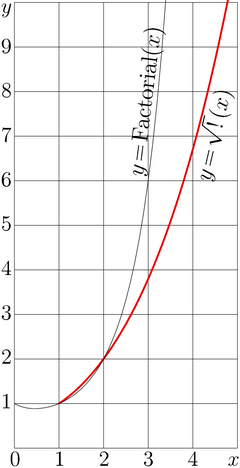
Square root of factorial
Square root of factorial (half-iteration of Factorial), or \(\sqrt{\ !\ }\) is solution \(h\) of equation
\[h(h(z))=z!\]
Square root of factorial is described in chapter 8 of book «Superfunctions»[1][2]
in order to give sense of the LOGO of the Physics department
of the Moscow State University; but also as an example of non-integer iterate of a growing holomorphic function (Factorial) treated as a Transfer function.
\(\sqrt{!\,}(z)= \sqrt{\mathrm{Factorial}}(z) =\ \)Factorial\(^{1/2}(z)\ \) should not be confused with
\(\sqrt{z!}=\sqrt{\mathrm{Factorial}(z)} =\big( \)Factorial\((z) \big)^{1/2} \ \)
nor with \(\sqrt{z}\ ! = \)Factorial\((z^{1/2}) \ \).
General view
It is assumed, that \(h\) is holomorphic function al least in some vicinity of halfline along the real axis, \(h\circ h=\mathrm{Factorial}\).
It is assumed that \(z\!=\!2\) is regular point of \(\sqrt{!\,}(z)\), and \(\sqrt{!\,}(2)=2\). Along the real axis, the square root of factorial grows faster than any polynomial, but slower than any exponential.
The square foot of factorial appears as the half iteration of factorial. Such a half iterate can be expressed through the superfactorial \(F\) and the Abelfactorial \(G\), which are the superfunction and the Abel function of factorial:
- \(\sqrt{!\,}(z)=F\left(\frac{1}{2}+G(z)\right)\)
Similar representation can be written using the Schroeder function of Factorial.
Square root of factorial is constructed in 2009 at the Institute for Laser Science, Japan, and described [3] in collaboration with Henryk Trappmann from the Berlin University, Germany.
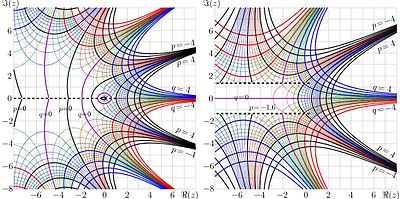
Complex maps: \(p\!+\!\mathrm iq\!=\!\sqrt{!}(z)\) and \(p\!+\!\mathrm iq\!=\!\sqrt{\exp}(z)\) by [3]
The complex map of the Square root of factorial is compared to that of the Square root of exponential in figure at right.
Other interpretations
The term square root of factorial is not so good and causes confusions. Some colleagues interpret the square root of factorial as function \(z \mapsto \sqrt{z!~}~\). However, it this case, it is difficult to understand, why is it interesting, why one used to claim that it has no physical meaning, and why such a function needs a special name.
In future, the name Half iteration of Factorial may be better to use instead of "Square root of factorial".
History

Creation of symbol
Since year, approхimately, 1950, the character \(\sqrt{!\,}\) is used as logo of the Physics department of the Moscow State University [4] . That time, the concept of square root of a function was considered as a nonsense, several authors claim that \(\sqrt{!\,}\) has no meaning [5][6].
Kneser and the pre-historic mathematicians
Perhaps, because of the Iron Curtain, the soviet colleagues did not know, that in Germany, the great mathematician Helmuth Kneser works on the \(\sqrt{\exp}\), and, to the year 1950, already has certain achievements in this area [7]. At least, Kneser had proved, that there exist hlomorphic function \(\varphi\) such that \(\varphi(\varphi(z))=\exp(z)\) in wide range of values of \(z\). The Kneser's function is even entire, but it is not real along the real axis, and Kneser did not provide any plot of his function. Kneser boiled up the old works by Heils Henryk Abel and Ernst Schröder (even in his time, those works were pretty old), that gave the hint to the evaluation of any, even the non-integer (and even complex) iteration of almost every holomorphic function.
Both the square root of factorial and the square root of exponential appear approximately in year 1950.
That time, there was no implementations for these functions that would allow to plot their complex maps.
The first attempt to analyze \(\sqrt{!\,}\) refers to year approximately 1978; such a function was suggested as one of the complementary (id est "very difficult") problems in the course of non-relativistic Quantum Mechanics by Vladimir Krivchenkov and Pavel Elutin. However, that time, none of students, nor even professors had advanced in the evaluation.
Breakthrough in century 21
It would be natural, first, to drill works by Schroeder and Abel, to analyze the \(\sqrt{\exp}\) by Kneser [7], then to consider the simple example of the logistic operator and the holomorphic extension of the logistic sequence [8], then to formulate the general theory of the regular iterations [9]; then, with this theory, to make the efficient algorithm for the tetration to base \(b\!<\! \exp(1/\mathrm e)\) [10], construct the general theory of regular iteration, and apply it to the evaluation of the SuperFactorial \(F\) and the AbelFactorial \(G\) [3]. Then, the square root of factorial, as half iterate of factorial, can be expressed as follows:
- \((1)~ ~ ~ \sqrt{!\,}(z)= F(1/2+G(z))\)
Practically, the events happened in a reverse order. First, the most complicated case with natural tetration was considered [11] and the algorithms for the efficient evaluation were suggested [12], then it was revealed that these algorithms cannot be used to evaluate theration to base \(b=\sqrt{2}\), and the regular iteration was developed [10][9]. In parallel, the holomorphic SuperFactorial and AbelFactorial were implemented [3] . These two functions allow to express the \(\sqrt{!\,}\). En in fin, by the request from Pawel Elutin, this stuff was applied to evaluate the holomorphic extension of the logistic sequence [8], with the resulting square root of the logistic operator; with all the tools prepared, the last step is pretty straightforward and easy, compared to the real-holomorphic \(\sqrt{\exp}\) and the \(\sqrt{!\,}\).
Superfactorial and Abelfactorial
The Superfactorial() is solution of the transfer equation
- \( (2) ~ ~ ~ F(z\!+\!1)=\mathrm{Factorial}(F(z))\)
holomorphic at least in the left hand side part of the complex plane, such that
- \( (3) ~ ~ ~ \displaystyle \lim_{x \rightarrow -\infty} F(x+\mathrm i y)=2 \)
The AbelFactorial \(G=F^{-1}\), id est, inverse function of SuperFactorial. The AbelFactorial satisfies the Abel equation
- \( (4) ~ ~ ~ G(z!)=G(z)+1 \)
For the convenience it is assumed that \(F(0)=3\); hence, \(G(3)=0\).
With SuperFactorial \(F\) and AbelFactorial \(G\), the \(c\)th iteration of factorial can be expressed as follows:
- \( (5)~ ~ ~ \mathrm{Factorial}^{c}(z)=F(c+G(z))\)
This representation can be used not only for integer \(c\) but also for the reals and even for complex values of \(c\). In particular, for \(c\!=\! 1/2\), this gives the \(\sqrt{!\,}\) as halfiteration of factorial.
Nest
In Mathematica, the square root of Factorial could be expressed through the function Nest,
- \(\sqrt{!\,}(z)=\mathrm{Factorial}^{1/2}(z)= \mathrm{Nest}\left(\mathrm{Factorial}, z,\frac{1}{2}\right)\)
The first argument of the Nest function is interpreted as name of iterated function, and the last argument is interpreted as number of iterations [13]. Unfortunately, the implementation of function Nest in version "Mathematica 8" does not support the use in general case; the only case supported is when the last argument is expresed with (or can be simplified to) a natural number, constant. The intents to use the Nest function with any other expressions as the last argument cause the error message. (For this reason, the C++ implementations of SuperFactorial and AbelFactorial were used to plot graphics.) One may expect, in the future versions of Mathematica, this fault will be corrected - at least for a function that allows to express its superfunciton and the abelfunction in terms of special functions. Then Mathematica's Nest will be easy-to-use tool for the evaluation of arbitrary (not necessary integer) iteratess of functions and algebraic analysis of such iterates.
References
- ↑ https://www.amazon.co.jp/Superfunctions-Non-integer-holomorphic-functions-superfunctions/dp/6202672862 Dmitrii Kouznetsov. Superfunctions: Non-integer iterates of holomorphic functions. Tetration and other superfunctions. Formulas,algorithms,tables,graphics - 2020/7/28
- ↑ https://mizugadro.mydns.jp/BOOK/468.pdf Dmitrii Kouznetsov (2020). Superfunctions: Non-integer iterates of holomorphic functions. Tetration and other superfunctions. Formulas, algorithms, tables, graphics. Publisher: Lambert Academic Publishing.
- ↑ 3.0 3.1 3.2 3.3 http://www.springerlink.com/content/qt31671237421111/fulltext.pdf?page=1 D.Kouznetsov, H.Trappmann. Superfunctions and square root of factorial. Moscow University Physics Bulletin, 2010, v.65, No.1, p.6-12
- ↑ http://zhurnal.lib.ru/img/g/garik/dubinushka/index.shtml Logo of the Physics Department of the Moscow State University. (In Russian);
- ↑ http://ofvp.phys.msu.ru/pdf/Kandidov_70.pdf: V.P.Kandidov. About the time and myself. (In Russian) «.. По итогам студенческого голосования победителями оказались значок с изображением рычага, поднимающего Землю, и нынешний с хорошо известной эмблемой в виде корня из факториала, вписанными в букву Ф. Этот значок, созданный студентом кафедры биофизики А.Сарвазяном, привлекал своей простотой и выразительностью. Тогда эмблема этого значка подверглась жесткой критике со стороны руководства факультета, поскольку она не имеет физического смысла, математически абсурдна и идеологически бессодержательна. ..»
- ↑ http://nauka.relis.ru/11/0412/11412002.htm 250 anniversary of the Moscow State University. (In Russian) ПЕРВОМУ УНИВЕРСИТЕТУ СТРАНЫ - 250! «.. На значке физфака в букву "Ф" вписано стилизованное изображение корня из факториала (√!) - выражение, математического смысла не имеющее. ..»,
- ↑ 7.0 7.1 http://www.digizeitschriften.de/dms/img/?PPN=GDZPPN002175851 H.Kneser. Reelle analytische Lösungen der Gleichung φ(φ(x))=ex. Equationes Mathematicae, Journal fur die reine und angewandte Mathematik {\bf 187} 56–67 (1950)
- ↑ 8.0 8.1 http://www.springerlink.com/content/u712vtp4122544x4 D.Kouznetsov. Holomorphic extension of the logistic sequence. Moscow University Physics Bulletin, 2010, No.2, p.91-98
- ↑ 9.0 9.1 http://www.springerlink.com/content/u7327836m2850246/ H.Trappmann, D.Kouznetsov. Uniqueness of Analytic Abel Functions in Absence of a Real Fixed Point. Aequationes Mathematicae, v.81, p.65-76 (2011)
- ↑ 10.0 10.1 http://www.ams.org/journals/mcom/2010-79-271/S0025-5718-10-02342-2/home.html D.Kouznetsov, H.Trappmann. Portrait of the four regular super-exponentials to base sqrt(2). Mathematics of Computation, 2010, v.79, p.1727-1756.
- ↑ http://www.ams.org/mcom/2009-78-267/S0025-5718-09-02188-7/home.html D.Kouznetsov. Analytic solution of F(z+1)=exp(F(z)) in complex z-plane. Mathematics of Computation, v.78 (2009), 1647-1670.
- ↑ http://www.ils.uec.ac.jp/~dima/PAPERS/2010vladie.pdf D.Kouznetsov. Superexponential as special function. Vladikavkaz Mathematical Journal, 2010, v.12, issue 2, p.31-45.
- ↑ http://reference.wolfram.com/mathematica/ref/Nest.html
Keywords
«Abelfactorial», «Gamma function», «Superfactorial», «Superfunctions», «Square root of exponential», «Square root of factorial», «Корень из факториала»,