Natural tetration
Natural tetration is tetration to base \(\mathrm e=\exp(1)\approx 1.71~\).
Natural tetration is denoted as \(\mathrm {tet}\) or \(\mathrm {tet}_{\mathrm e}\); it satisfies the transfer equation
- \(\exp(\mathrm{tet}(z))= \mathrm{tet}(z\!+\!1)\)
Also the initial condition \(\mathrm{tet}(0)=1\) and behavior at \(\rm i\infty\) is assumed; the tetration approaches the fixed points \(L\) and \(L\)^* of exponential.
History
Existence of natural tetration been indicated in 1950 by Hellmuth Kneser in 1950 [2]. Keser indicated, that the natural tetration can be constructed for the holomorhix solution \( \varphi\) of equation
\( \varphi(\varphi(x))=\mathrm e^x \).
Since that, during 60 years, no efficient algorithm for the evaluation had been reported. Then the natural tetration and tetrations to other bases had been plotted.
Hisotrically, the natural tetration appears to be first non-trivial superfunction, that had been precisely evaluated with numerical solution of the Transfer equation \( \mathrm{tet}(z\!+\!1)=\exp(\mathrm{tet}(z)) \). The, the same had been done for tetrations to other values of baze and for other funcitons, including factorial and polunomials.
Asympotics
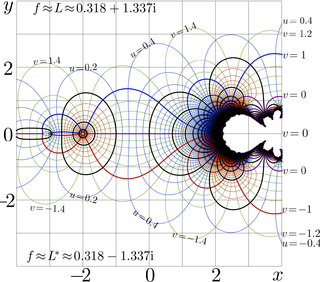
The asymptotic behavior at large values of the imaginary part of the argument is exponential approach the fixed point \(L\) of logarithm
\(\!\!\!\! L=\mathrm{Filog}(1)\approx 0.31813150520476413531+1.3372357014306894089\, i \)
in the upper half-plane and
\(L^*\)
in the lower half-plane. See the spacial article Filog about this constant.
Evaluation
Natural tetration can be evaluated with the Iterated Cauchi algorithm [3].
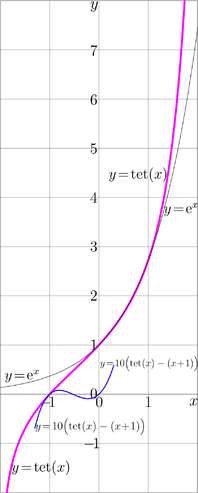
Along the real axis, the natural tetration shows fast growth, faster than any exponential and faster than any finite combinaiton of exponentials.
Function \(\mathrm {tet}(z)\) is holomorphic in the whole complex plane except the line \(\Re(z)\le -2\). Due to the wide range of holomorphism, and the simple properties, tetration is most important among various superfunctions of the exponential; an other supedfunciotn can be expressed with
- \(\mathrm{sexp}(z)=\mathrm{tet}(z+\eta(z))\)
where \(\eta\) is holomorphic periodic function with period unity, The exponential growth of \(\eta(z)\) in the direction of the imaginary axis reduces the range of holomorphism of such a superexponential, destroying its apymptotic approach to \(L\) and \(L^*\).
Inverse of the natiral tetration is denoted with symbol \(\mathrm {ate}=\mathrm {tet}^{-1}\).
The pair of functions \(\mathrm {tet}\) and \(\mathrm{ate}\) allows the efficient evaluation of the iteration of exponential,
- \(\exp^c(z)=\mathrm{tet}(c+\mathrm{ate}(z))\)
The number \(c\) of iterations has no need to be integer; in particular, it can be a fration, an irrational number of even a complex number.
The non–integer iterations of exponential give the class of functions that grow faster than any polynomial but slower than any exponential.
Approximations with elementary functions
Several approximations of tetration and arctetration are described [3][4].
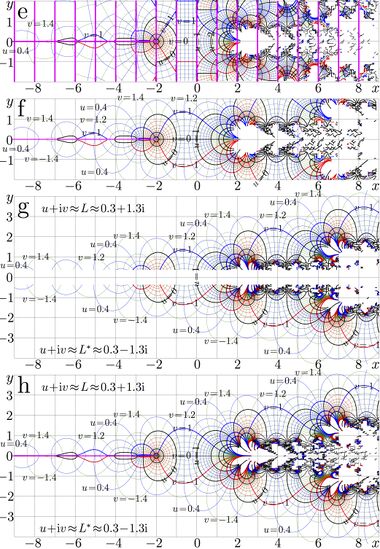
Complex maps for four such approximations of tetration are shown in figure at left. Numeration of maps begins with letter e, in order to avoid confusion with similar figure 1 from [3], where equilimes of logamplitude and phase are drown, instead of real and imaginary parts in figure at right. The numbering letters are placed in the top left corner of each map.
Due to the transfer equation, the change from logamplitude and phase to real and imaginary part are almost equivalent to the translation of all the map for unity along the real axis. Natural tetration seems to be the only non-trivial function with this property.
Map e at the top of the figure corresponds to the "linear" approximation \(f=\mathrm{uxp}\) by M.H.Hooshmand
[5]
\( \displaystyle \!\! f(z)=\mathrm{uxp}(z)=\!\left\{ \begin{array}{ccccccc} \ln\!\big({\rm uxp}(z\!+\!1)\big) &{\rm at} &~ \!&\! \!&\! \Re(z) \!&\! \le \!&\!\! -1\! \\ z + 1 &{\rm at} & -1 \!&\! < \!&\! \Re(z) \!&\! \le \!&\! 0 \\ \exp\!\big({\rm uxp}(z\!-\!1)\big) &{\rm at} &~ 0 \!&\! < \!&\! \Re(z) \!& \end{array} \right. \)
The sequence of vertical cutlines separate the complex plane to the set of almost iindependent strips, where the approximation is holomorphic. This cutting was one of motivations to build-up the real-holomorphic tetration tet.
Map f corresponds to the approximation \(\mathrm{Fit}_3\) constructed in the following way:
\(s_2(z)= \exp\!\Big(\exp(z-2.51)\Big)-0.6+0.08(z\!+\!1)\)
\(\mathrm{fit}_2(z) \!=\!\) \( \ln(2\!+\!z) + (1\!+\!z)\left( 1 + \frac{z}{2}\exp\!\Big((z\!-\!1)s_2(z)\Big) \Big(\!\mathrm e\! -2\! +\! \ln\frac{4}{3} \Big) - \ln 2 \right)\)
\(\mathrm{fit}_3(z)=0.6\!~\mathrm{fit}_{2}(z)+0.4\!~\ln\big( \mathrm{fit}_{2}(z+1)\big)\)
\(\mathrm{Fit}_3(z)= \left\{\!\! \begin{array}{ccccc cc} \ln\!\big({\rm Fit}_{3}(z\!+\!1)\big) &{~\rm at}&~ \!&\! \!&\! \Re(z) \!&\! \le \!&\! -1 \!\\ \mathrm{fit}_{3}(z) &{~\rm at}& -1 \!&\! < \!&\! \Re(z) \!&\! \le \!&\! 0 \!\\ \exp\!\big({\rm Fit}_{3}(z\!-\!1)\big) &{~\rm at}&~ 0 \!&\! < \!&\! \Re(z) \!& \end{array} \right.\)
Constants in definition of function \(s\) have rather historical than mathematical meaning, because they were used to guess the asymptotic behavior of tetration, while the precise algorithm for the evaluation had not yet been discovered. Using the precise implementation, the approxximation can be improved.
Map g corresponds to the asymptotic representation
\(f(z)=\mathrm{fit}_6(z) =\) \( \left\{ \begin{array} ~ L+\exp(kz+r) ~, ~ \Re(z)<-8\\ \exp\Big(\mathrm{fit}_6(z\!-\!1)\Big)~,~ \Re(z)\ge -8 \end{array} \right.\)
for \(\Im(z)>0.5\) and \(f(z)=\mathrm{fit}_6(z^*)^*\) for \(\Im(z)<0.5\) ; In the map, the strip of intermediate values \(|y|<1/2\) is left empty. In formula above, \(L\approx 0.31813150520476413 + 1.3372357014306895 \,\mathrm i\) is fixed point of logarithm, \(L=\ln(L)\). For Natural tetration, the increment \(k=L\). Parameter \(r\) provides the match of the two asymptotics. It is fundamental mathematical constant; \(r \approx 1.075820830781 - 0.9466419207254 \, \mathrm i\) . This precision seems to be sufficient for the applications; however, the improvement of the precision may be subject of the additional research.
Map h shows the precise implementation of tetration with 14 decimal digits through the Cauchi integral [3].
In principle, the approximations \(\mathrm{Fit}_3\), shown in map e, and \(\mathrm{Fit}_6\), shown in map f, allow to implement tetration in the whole complex plane with at least 3 defimal figures; this precision is sufficient to make camera–ready illustrations of properties of tetration. Historically, approximations \(\mathrm{fit}_6\) and \(\mathrm{Fit}_6\) were obtained after to implement the tetration through the Cauchi integral, when not only the limiting value \(L\) of tetration had been revealed, but also the exponential approaching of tetration to this value.
Numerical implementation
Up to date, the most reliable complex double implementation of natural tetration tet in C++ is loaded as fsexp.cin, and called FSEXP. This name happened to be not woo good, because the search engines for this name offer many cites that have nothing to do with super functions, exponentials, nor even mathematics. I hope, the improved implementation will have more suitable name.
Implementation of the corresponding arctetration is loaded as fslog.cin. The name of the routine, FSLOG, corresponds the the idea to name arctetration with identifier "super logarithm". The name Superlogarithm causes confusions, it makes an impression that it is superfunction of logarithm. One superfunction \(G\) of logarithm can be expressed through the tetration, namely, \(G(z)=\mathrm{tet}(-z)\), which is not arctetration. For this reason, the name "fslog" is not good. However, for the historic reason, the name of the routine remains. As soon as the most efficient algorithms for evaluation of tetration and arctetration will be implemented, the implementations may have more understandable names TET and ATE.
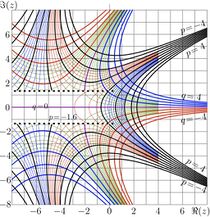 \( p\!+\!\mathrm i q=\varphi(z) \) [6]
\( p\!+\!\mathrm i q=\varphi(z) \) [6]
Square root of exponential
Tetration tet and arctetration ate allow to express the non-integer iterates of the exponential:
\( \exp^n(z)=\mathrm{tet}(n+\mathrm{ate}(z)) \)
In praticilar, for \(n=1/2 \), this formula gives the square root of exp, or iteration half of exponent, id est, holomorphic function \(\varphi\) such that
\( \varphi(\varphi(z)) = z ~ \) in wide range of values of \( z \).
This function is mentioned in the title of article [2] by Hellmuth Kneser.
The complex map of function \(\varphi\) had been constructed in 2009; its map is shown in figure at left.
Fixed points and Superfunction
For natural tetration, the real fixed point \(L_{\mathrm e,4,0} \!=\! L_{\mathrm e, 4,0} \!\approx\! -1.8503545290271812\) is used to construct the superfunction of tetration, the fifth Ackermann function, called natural pentation;
\(\mathrm{pen}=A_{\mathrm e,5}\)
For pentation, the tetration tet is interpreted as the transfer function. Pentation satisfies the transfer equation
\(\mathrm{pen}(z\!+\!1)=\mathrm{tet}\Big(\mathrm{pen}(z)\Big)\)
References
- ↑ https://opc.mfo.de/detail?photo_id=7607 On the Photo: Kneser, Hellmuth Location: Oberwolfach Author: Danzer, Ludwig (photos provided by Danzer, Ludwig) Source: L. Danzer, Dortmund Year: 1958 Copyright: L. Danzer, Dortmund Photo ID: 7607
- ↑ 2.0 2.1 http://www.digizeitschriften.de/dms/img/?PID=GDZPPN002175851&physid=phys63#navi Hellmuth Kneser. Reelle analytische Lösungen der Gleichung \( \varphi(\varphi(x))=\mathrm e^x \) und verwandter Funktionalgleichungen. Journal für die reine und angewandte Mathematik / Zeitschriftenband (1950) / Artikel / 56 - 67
- ↑ 3.0 3.1 3.2 3.3
http://www.ams.org/mcom/2009-78-267/S0025-5718-09-02188-7/home.html
http://www.ils.uec.ac.jp/~dima/PAPERS/2009analuxpRepri.pdf D.Kouznetsov. Analytic solution of F(z+1)=exp(F(z)) in complex z-plane. Mathematics of Computation, v.78 (2009), 1647-1670. - ↑
http://www.vmj.ru/articles/2010_2_4.pdf
D.Kouznetsov. Superexponential as special function. Vladikavkaz Mathematical Journal, 2010, v.12, issue 2, p.31-45, In Russian. English version:
http://www.ils.uec.ac.jp/~dima/PAPERS/2010vladie.pdf
https://mizugadro.mydns.jp/PAPERS/2010vladie.pdf - ↑ http://www.tandfonline.com/doi/full/10.1080/10652460500422247 M. H. Hooshmand, (2006). "Ultra power and ultra exponential functions". Integral Transforms and Special Functions 17 (8): 549–558. %doi:10.1080/10652460500422247.
- ↑
https://link.springer.com/article/10.3103/S0027134910010029
https://mizugadro.mydns.jp/PAPERS/2010superfae.pdf (English)
https://mizugadro.mydns.jp/PAPERS/2010superfar.pdf (Russian)
D.Kouznetsov, H.Trappmann. Superfunctions and square root of factorial. Moscow University Physics Bulletin, 2010, v.65, No.1, p.6-12. (Russian version: p.8-14)
https://link.springer.com/article/10.1007%2Fs00010-010-0021-6 H.Trappmann, D.Kouznetsov. Uniqueness of holomorphic Abel functions at a complex fixed point pair. Aequationes Mathematicae, v.81, p.65-76 (2011)
http://link.springer.com/article/10.1007/s10444-017-9524-1 William Paulsen and Samuel Cowgill. Solving \(F(z+1)=b^{F(z)}\) in the complex plane. Advances in Computational Mathematics, 2017 March 7, p. 1–22
http://en.citizendium.org/wiki/Tetration
Keywords
Ackermann function, Exponential, exp, Fixed point, fsexp.cin, fslog.cin, Superfunction, Tetration, Transfer equation, Superfunction, Superfunctions