Filog
Filog is holomorphic function that expresses the fixed points of logarithm to complex base.
\(f=\mathrm{Filog}(z)\) is solution of the equation
- \(\log_b(f)\!=\!f\)
for base \(b\!=\!\exp(z)\).
Another fixed point to the same base can be expressed with \(\mathrm{Filog}(z^*)^*\)
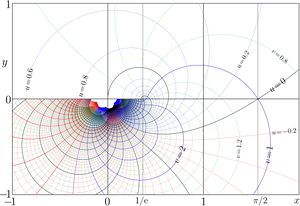
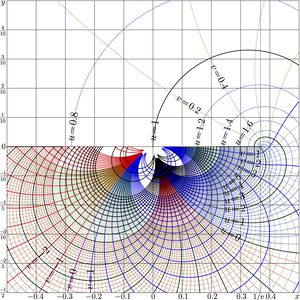
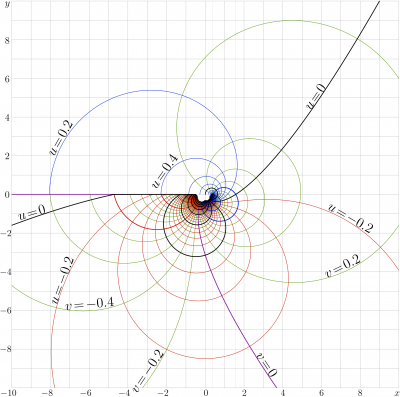
Complex map of Filog
\(f=\mathrm{Filog}(x+\mathrm{i} y)\) is shown in the \(x,y\) plane with levels \(u\!=\!\Re(f)\!=\!\mathrm{cont}\) and levels \(v\!=\!\Im(f)\!=\!\mathrm{cont}\); thick lines correspond to the integer values.
The additional thin gridlines \(x\!=\!\exp(-1)\) and \(x\!=\!\pi/2\) are drawn. The first of them goes through the branchpoint \(z=1/\mathrm e\); the second goes through the point \(z\!=\!\pi/2\), where the fixed points of logarithm are \(\pm \mathrm i\).
Properties of the function
\(\mathrm{Filog}(z)\) has the branch point at \(~z\!=\!\exp(-1)~\); the cutline is directed to the negative part of the real axis.
The lower list has also singularity, at \(~z\!=\!0~\).
Except the cutline, the function is holomorphic. At the real values of the argument \(0\!<\!z\!<\!\exp(-1)\), both at the upper side of the cut and at the lower side of the cut, the function has real values; in addition, at \(z=\ln\big(\sqrt{2}\big)\), these values are integer [1]:
- \(\mathrm{Filog}(z+\mathrm i o)=2\)
- \(\mathrm{Filog}(z-\mathrm i o)=4\)
At the branchpoint, the jump at the cut vanishes:
- \( \displaystyle \lim_{x\rightarrow 1/\mathrm e} \mathrm{Filog}(x+\mathrm i o)= \lim_{x\rightarrow 1/\mathrm e} \mathrm{Filog}(x-\mathrm i o)= \mathrm e\)
Relation with Tania function
Filog can be expressed through the Tania function and with the WrightOmega function.
For moderate valus of \(\Im(\ln (z))\), the relation through function WrightOmega can be used
\(\displaystyle \mathrm{Filog}(z)= \frac{\mathrm{WrightOmega}\!\big(\ln(z)-\pi \mathrm{i}\big)}{-z}\)
More robust is relation through the Tania function,
\(\displaystyle \mathrm{Filog}(z)= \frac{\mathrm{Tania}\!\big(\ln(z)-1- \pi \mathrm{i}\big)}{-z} \)
where Tania function is solution of equations
\(\displaystyle \mathrm{Tania}'(z)=\frac{\mathrm{Tania}(z)}{1+\mathrm{Tania}(z)} ~ ~,\) \( ~ ~ ~ \mathrm{Tania}(0)=1\)
The efficient implementation for the Tania function is available. The representation through the Tania function above is used for the evaluation (and plotting) of the Filog function.
The Tania function has slow growth at infinity, and Filog at infinity decays to zero:
- \(\displaystyle \lim_{|z|\rightarrow \infty} \mathrm{Filog}(z) =0 \)
Application of Filog
Filog is important for the evaluation of tetration of complex argument: in the upper half-plane, the tetration to base \(b\!=\!\exp(a)\) should asymptotically approach to value \(\mathrm{Filog}(a)\), while in the lower half-plane, the limiting value should be \(\mathrm{Filog}(a^*)^*\).
References
- ↑ http://www.ams.org/journals/mcom/2010-79-271/S0025-5718-10-02342-2/home.html D.Kouznetsov, H.Trappmann. Portrait of the four regular super-exponentials to base sqrt(2). Mathematics of Computation, 2010, v.79, p.1727-1756.