Tetration
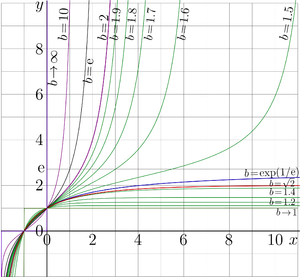


Tetration (Тетрация) is the superfunction of the exponential map. For a given base \(b\), the tetration \(\operatorname{tet}_b\) is defined as the function satisfying the transfer equation \[ \operatorname{tet}_b(z+1) = b^{\operatorname{tet}_b(z)} \] together with additional normalization and regularity conditions that select a unique solution among infinitely many possible superfunctions. For real values of the argunet, the explicit plots of \(\operatorname{tet}_b(x)\) versos \(x\) for various real values of base \(b\) is shown in figure at right.
The inverse function ArcTetration is denoted with symbol ate; \( \mathrm{ate}_b = \mathrm{tet}_b^{-1} \).
The iterates of Exponential can be expressed as follows:
\(
\exp_b^{\ n}=\operatorname{tet}_b\big(n+\operatorname{ate}_b(z)\big)
\).
Here, number \(n\) of the iterate has no need to be integer. In particular, \(\varphi=\exp^{1/2}\)
appears as solution of equation \( \varphi(\varphi(x))=\mathrm e^x \); this equation had been considered by Hellmuth Kneser [3], 1950.
Notations
The name tetration reflects its role as the next operation after exponentiation within the hyperoperation hierarchy:
Ackermann\(_1\), id est, the Addition appears as superfunction of unity increment;
Ackermann\(_2\), id est, the Multiplication appears as superfunction of additon;
Ackermann\(_3\), id est, the Exponential \(\exp\) appears as superfunction of multiplication;
Ackermann\(_4\), id est, the Tetration \(\mathrm{tet}\) appears as superfunction of exponential;
Ackermann\(_5\), id est, the Pentation \(\mathrm{pen}\) appears as superfunction of tetration;
and so on. These functions are qualified as ackermanns after the last name of
mathematician Wilhelm Ackermann.
The most studied case is the Natural tetration
[4][5]. It corresponds to base \(b=\mathrm e\); it can be written simply as
\[
\operatorname{tet}(z)=\operatorname{tet}_{\mathrm e}(z).
\]
For base \(\mathrm e\) the first five ackermanns are shown in figure at right.
The dashed line refers to the natural tetration.
In such a way, all the ackermanns are numerated.
In notation Ackermann\(_m (z)\), the number \(m\) is supposed to be positive integer (natural number).
To year 2025, the generalization of Ackermann\(_m(z)\) for non-integer values of \(m\) is not yet developed.
However, the argument \(z\) may have complex values.
Complex maps of tetration to various bases are shown in figures below. Lines \(u=\mathrm{const} \) and lines \(v=\mathrm{const} \) are drawn for \(u+\mathrm i v=\mathrm{tet}_b(x\!+\!\mathrm i y)\).
Definition
Let \(T_b(z)=b^z\). A function \(F\) is a superexponential (a superfunction of \(T_b\)) if \[ F(z+1) = T_b(F(z)). \]
A tetration to real base \(b\) is real-holomorphic superexponential \(F\) such that \(F(x+\mathrm i y)\) remains bounded at \(y\to\pm\infty\) and \(F(0)=1\).
Such a solution is believed to exists and to be unique [6][7].
Special cases


Decimal tetration, \(b=10\). The routine for the evaluation is loaded as F4ten.cin. It is used to plot the top picture.
Natural tetration, \(b=\mathrm e\). The complex map for this case is shown in figure above. The original description [4] and the fast C++ implementation [5] are published and mentioned in book Superfunctions [2]
Binary tetration, \(b=2\), see Base 2
tetration to base 1.5, see Base 1.5
Crytical tetration, \(b= \mathrm e^{1/\mathrm e}\), see Base e1e
Tetration to base sqrt2, \(b= \sqrt{2}\), see Base sqrt2
Tetration to Sheldon base \(b=1.52598338517+0.0178411853321\ \mathrm i\). The original algorithm [4] allows the straight-forward generalization for the case of complex values of base \(b\). After the request by Sheldon Levenstain, the complex map of this tetration had been generated; it is shown in figure at right.
Continuity at base b=exp(1/e)
This cartoon at right illustrates a philosophical point in tetration theory:
"The only we may conclude, that in this county, there is at least one sheep,
and at least the right-hand side of this animal is black".
The heuristic assumptions that appear “obvious’’ (e.g., that the right side of a sheep has the same color as its left side) appears without rigorous proof and, from point of a mathematician, may happen to be wrong.
The similar heuristic assumption refers to the continuity of tetration \(\mathrm{tet}_b(z) \) being considered as function of base \(b\) at point \(b=\exp(1/\mathrm e)\).
The maps above for \(b=1.5\), \(b=\exp(1/\mathrm e)\approx 1.44\) and \(b=\sqrt{2}\approx 1.41\) as well as the explicit plot at the top make an impression, that the tetration is continuous and perhaps holomorphic with respect to \(b\) at this point: the variation in the 3d significant figure causes small change of the view of the curves; at least for moderate valies of argument \(z\)
As in the case of the sheep in the cartoon, this assumptions about tetration is not obvious and require careful justification.
The preliminary numerical analysis indicates, that
\(\mathrm{tet}_b(z)\) for \(\Re(b)<\exp(1/\mathrm e)\)
is not analytical extension of
\(\mathrm{tet}_b(z)\) for \(\Re(b)>\exp(1/\mathrm e)\);
in the simplest way, the cut line along line \(\Re(b)=\exp(1/\mathrm e)\)
divides the complex plane to two almost independent parts,
and only in point \(b=\exp(1/\mathrm e)\), these two tetrations have the same limiting
tetration.
However, the cut at the complex \(b\)-plane has no need to follow the vertical line \(\Re(b)=\exp(1/\mathrm e)\); but this choice is simplest and has priority (following the last, 6th of the TORI axioms.)
Applications
The obvious application of the tetration may refer to representation of huge numbers.
For example the Googolplex number [8] can be expressed as follows:
\[
10^{10^{100}}=\mathrm{tet}_{10}^3(2)
\]
However, up to year 2025, Editor have not yet found any scientific concept
that deals with such a huge number.
The more realistic application may refer to the approximation of processes that grows faster than any polynomial but slower than any exponential. The non-integer iterates greatly extend the arsenal of functions available for construction of efficient fits, involving less fitting parameters and/or providing better precision and/or having wider range of approximation.
The \(n\)-th iterate of the exponential: \[ \exp_b^{\ n}(z) = \operatorname{tet}_b\!\big(n + \operatorname{ate}_b(z)\big), \] for real \(n\). One example of such a function is mentioned in the Preamble.
An additional extension could be generalization of ackermann\(_m\)
to non-integer values of \(m\), looking for the real-holomorphic solition \(A\) of equations
\[
A_m(z+1)=A_{m-1}(A_m(z)) \\
A_2(z)= \mathrm e\ z \\
Z_m(0)=1 \text{ for } m>2
\]
treating \(A_m(z)\) as holomorphic function of two variables \(m\) and \(z\).
Such a generalization can be matter for the future research.
Acknowledgement
ChatGPT helped to improve this article.
References
- ↑ 1.0 1.1 1.2 1.3 https://mizugadro.mydns.jp/BOOK/202.pdf Дмитрий Кузнецов. Суперфункции. Lambert Academic Publishing, 2014
- ↑ 2.0 2.1 2.2 2.3 2.4 2.5 2.6
https://www.amazon.co.jp/Superfunctions-Non-integer-holomorphic-functions-superfunctions/dp/6202672862
https://mizugadro.mydns.jp/BOOK/468.pdf Dmitrii Kouznetsov. Superfunctions. Lambert Academic Publishing, 2020. - ↑ http://www.digizeitschriften.de/dms/img/?PID=GDZPPN002175851&physid=phys63#navi Hellmuth Kneser. Reelle analytische Lösungen der Gleichung \( \varphi(\varphi(x))=\mathrm e^x \) und verwandter Funktionalgleichungen. Journal für die reine und angewandte Mathematik / Zeitschriftenband (1950) / Artikel / 56 - 67
- ↑ 4.0 4.1 4.2
https://www.ams.org/journals/mcom/2009-78-267/S0025-5718-09-02188-7/home.html
http://mizugadro.mydns.jp/PAPERS/2009analuxpRepri.pdf Dmitrii Kouznetsov. Solution of F(z+1)=exp(F(z)) in complex z-plane. Mathematics of Computation, 2009, V.78, p.1647-1670. - ↑ 5.0 5.1
https://mizugadro.mydns.jp/PAPERS/2010vladie.pdf
https://www.vmj.ru/articles/2010_2_4.pdf
https://mizugadro.mydns.jp/PAPERS/2010_2_4.pdf D.Kouznetsov. Tetration as special function. (In Rusian) Vladikavkaz Mathematical Journal, 2010, v.12, issue 2, p.31-45. - ↑ https://link.springer.com/article/10.1007/s00010-010-0021-6 https://mizugadro.mydns.jp/2011uniabel.pdf H.Trappmann, D.Kouznetsov. Uniqueness of holomorphic Abel functions at a complex fixed point pair. Aequationes Mathematicae, v.81, p.65-76 (2011)
- ↑ https://math.stackexchange.com/questions/284868/uniqueness-of-tetration Let 𝑓(0)=1 and 𝑓(𝑥+1)=2^𝑓(𝑥) // Also let f be infinitely differentiable. Then does f exist and is it unique? // If f is merely continuous, then any continuous function such that f(0)=1 f(1)=2 satisfies the conditions(if f is defined in [0,1] ,we can use the property to define it everywhere else). Similar things can be said for differentiability. But I don't how to solve the problem if it's infinitely differentiable.
- ↑ https://en.wikipedia.org/wiki/Googolplex A googolplex is the large number \(10^{10^{100}}\), that is, 10 raised to the power of a googol. If written out in ordinary decimal notation, it would be 1 followed by a googol (10100) zeroes – a physically impossible number to write explicitly.
https://en.wikipedia.org/wiki/Ackermann_function This function is defined from the recurrence relation \(\operatorname{A}(m+1, n+1) = \operatorname{A}(m, \operatorname{A}(m+1, n)) \) with appropriate base cases.
https://en.wikipedia.org/wiki/Tetration In mathematics, tetration (or hyper-4) is an operation based on iterated, or repeated, exponentiation. There is no standard notation for tetration, though Knuth's up arrow notation \(\uparrow \uparrow\) and the left-exponent \({}^{x}b\) are common.
https://en.citizendium.org/wiki/Tetration Tetration is a rapidly growing mathematical function, which was introduced in the 20th century and proposed for the representation of huge numbers in the Mathematics of Computation.
https://tetrationforum.org/search.php?action=results&sid=094d9363dba94b4cfc99575883e4e5bb&sortby=&order=desc Tetration Forum
https://www.numdam.org/item?id=BSMF_1919__47__161_0 P. Fatou. Sur les ´equations fonctionnelles. Bulletin de la Soci´et´e Math´ematique de France, 47 (1919), p. 161-271.
https://eretrandre.org/rb/files/Ackermann1928_126.pdf Wilhelm Ackermann. Zum Hilbertschen Aufbau der reellen Zahlen. Mathematische Annalen 99, Number 1(1928), Z.118-133.
https://projecteuclid.org/journals/acta-mathematica/volume-100/issue-3-4/Regular-iteration-of-real-and-complex-functions/10.1007/BF02559539.full G.Szekeres. Regular iteration of real and complex functions. Acta Mathematica 1958, Volume 100, Issue 3-4, pp 203-258.
https://www.ams.org/journals/bull/1993-29-02/S0273-0979-1993-00432-4/S0273-0979-1993-00432-4.pdf W.Bergweiler. Iteration of meromorphic functions. Bulletin (New Series) of the American Mathematical society, v.29, No.2 (1993) p.151-188.
https://www.tandfonline.com/doi/full/10.1080/10652460500422247 M.H.Hooshmand, (2006). Ultra power and ultra exponential functions. Integral Transforms and Special Functions 17 (8): 549–558
https://sciencepublishinggroup.com/article/10.11648/j.acm.20140306.14 Dmitrii Kouznetsov. Evaluation of Holomorphic Ackermanns. Published in Applied and Computational Mathematics (Volume 3, Issue 6) Received: 21 November 2014 Accepted: 17 December 2014 Published: 27 December 2014, Page(s) 307-314.
https://www.proquest.com/openview/cb7af40083915e275005ffca4bfd4685/1?pq-origsite=gscholar&cbl=18750 Samuel Cowgill. EXPLORING TETRATION IN THE COMPLEX PLANE EXPLORING TETRATION IN THE COMPLEX PLANE A Thesis presented to the faculty of Arkansas State University in partial. fulfillment of the requirements for the Degree of MASTER OF SCIENCE IN MATHEMATICS ARKANSAS STATE UNIVERSITY //MAY 2017 Approved by: Dr. William Paulsen, Thesis Advisor Dr. Jie Miao, Committee Member Dr. Jeongho Ahn, Committee MemberPREVIE
https://link.springer.com/article/10.1007/s10444-018-9615-7 William Paulsen. Tetration for complex bases. Advances in Computational Mathematics. Published: 02 June 2018// Volume 45, pages 243–267, (2019)
https://www.researchgate.net/publication/325532999_Tetration_for_complex_bases
https://www.researchgate.net/figure/Level-curves-for-Rk-b-z-and-Ik-b-z-0-1-2-3-4-for-b-i_fig1_325532999
William Harold Paulsen. Tetration for complex bases.
Advances in Computational Mathematics 45(6),
February 2019
DOI:10.1007/s10444-018-9615-7
http://myweb.astate.edu/wpaulsen/tetration2.pdf William Paulsen and Samuel Cowgil. Solving F(z+1)=b^F(z) in the complex plane.
Keywords
«Abel function», «Ackermann», «ate», «Base e1e», «Base sqrt2», «Exponential», «Filog», «fit1.cin», «Fixed point», «Fsexp.cin», «Fslog.cin», «Hellmuth Kneser», «Iterates», «Iterate of exponential», «Maps of tetration», «Mathematics of Computation», «Logarithm», «Superfunction», «Superfunctions», «tet», «Tetration», «Transfer equation»,
