Doya function
The Doya function and its iterates appear as the transfer function of an optical amplifier with simplest kinetic model.
In vicinity of the real axis (While \(|\Im(z)| \!<\! \pi\)), the Doya function can be expressed through the LambertW function (called also "ProductLog")
- \(\displaystyle\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\! (1) ~ ~ ~ \mathrm{Doya}(z)=\mathrm{LambertW}\Big( z~ \mathrm{e}^{z+1} \Big)\)
The LambertW is build-in function in Mathematica, Maple, Matlab and perhaps many other languages.
Contents
Tania function
For the comlex argument, the Doya function can be defined in terms of the Tania function and its inverse function with equation
- \( \displaystyle \!\!\!\!\!\!\!\!\!\!\!\!\!\!\! (2) ~ ~ ~ \mathrm{Doya}(z)= \mathrm{Tania}\!\Big(1+\mathrm{ArcTania}(z)\Big)\)
where \(\mathrm{Tania}\) is solution of equations
- \(\displaystyle \!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\! (3) ~ ~ ~ \mathrm{Tania}'(z)= \frac{ \mathrm{Tania}(z)}{1\!+\!\mathrm{Tania}(z)}~\), \(~\mathrm{Tania}(0)\!=\!1\)
and ArcTania function is its inverse function, it can be expressed as
- \(\displaystyle\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\! (4) ~ ~ ~ \mathrm{ArcTania}(z)=z+\ln(z)-1\)
Also, for moderate values of the imaginary part of the argument, the Tania function can be expressed through the WrightOmega function,
- \(\displaystyle\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\! (5) ~ ~ ~ \mathrm{Tania}(z)=\mathrm{WrightOmega}(z\!+\!1)\)
However, for comparison of superfunctions \(F\) for various cases, it is convenient to keep relation \(F(0)=1\) (as it is accepted for tetration, which is superfunction of exponential); for this reason, the Tania function is used in TORI even after the "discovery" of its relation (5) with known function WrightOmega.
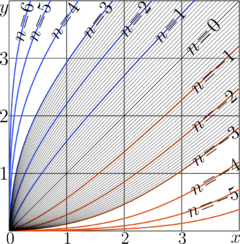
The top figure at right shows graphics of the \(t\)th iterate of Doya for
- \(t\!=\!3\), id est, \(~\mathrm{Doya}^3(x)=\mathrm{Doya}\Big(\mathrm{Doya}\big(\mathrm{Doya}(x)\big)\Big)\)
- \(t\!=\!2\), id est, \(~\mathrm{Doya}^2(x)=\mathrm{Doya}\big(\mathrm{Doya}(x)\big)\)
- \(t\!=\!1\), id est, \(~\mathrm{Doya}^1(x)=\mathrm{Doya}(x)\)
- \(t\!=\!0\), id est, \(~\mathrm{Doya}^0(x)=x\)
- \(t\!=\!-1\), id est, \(~\mathrm{Doya}^{-1}(x)=\mathrm{ArcDoya}(x)\)
and so on versus real \(x\). These iterates can be expressed through the Tania function and the ArcTania with slight modification of equation (2):
- \( \displaystyle \!\!\!\!\!\!\!\!\!\!\!\!\!\!\! (6) ~ ~ ~ \mathrm{Doya}^t(z)=\mathrm{Tania}\!\Big(t+\mathrm{ArcTania}(z)\Big)\)
As properties, as the numerical implementation of the Tania function are simpler than those of the LambertW function. For these reason, in TORI, the Tania function is considered as principal; both Doya function and the LambertW function are implemented through the Tania function.
the as Doya function, as Tania function
Doya function as transfer function
The Doya function is transfer function for the Tania function, id est, the Tania function is superfunction of the Doya function satisfying the transfer equation
- \(\displaystyle\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\! (7) ~ ~ ~ \mathrm{Doya}(\mathrm{Tania}(z))=\mathrm{Tania}(z\!+\!1)\)
This means that for the First Doya function, the Tania function is superfunction. In more general form, the same equation can be written as
- \(\displaystyle\!\!\!\!\!\!\!\!\!\!\!\!\!\! \!\!\! (8) ~ ~ ~ \mathrm{Doya}^t(\mathrm{Tania}(z))=\mathrm{Tania}(z\!+\!t)\)
at least in some vicinity of real values of \(z\) and \(t\).
In the similar way, for the Doya function, the ArcTania function is the Abel function, satisfying the Abel equation
- \(\displaystyle \!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\! (9) ~ ~ ~ \mathrm{ArcTania}\!\Big( \mathrm{Doya}(z)\Big)=\mathrm{ArcTania}(z)+1\)
As any transfer function, the Doya function commutes with its superfunction,
- \(\displaystyle \!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\! (10) ~ ~ ~ \mathrm{Doya}^t(\mathrm{Tania}(z))= \mathrm{Tania}(\mathrm{Doya}^t(z))=\mathrm{Doya}^{t+1}(z)\)
Properties of the Doya function
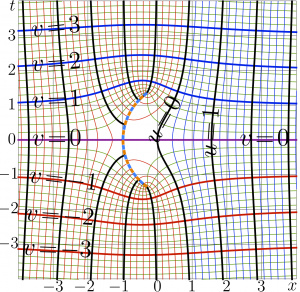
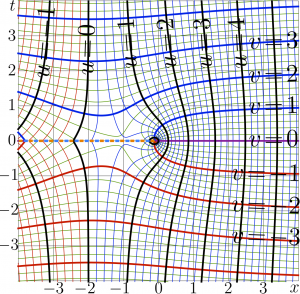
The complex map of the Doya function and its iterates is shown in figures at left; \(f\!=\!\mathrm{Doya}_t(x\!+\! \mathrm{i} y)\) is shown with Lines \(u\!=\!\Re(f)\!=\!\mathrm{const}\) and lines \(v\!=\!\Im(f)\!=\!\mathrm{const}\). However, \(F^{-1}(z)~\) should not be confused to \(F(z)^{-1}\!=\!\frac{1}{F(z)}\), and \(F^{2}(z)=F(F(z))~\) should not be confused to \(F(z)^{2}\!=\!\ F(z)\!\cdot\! F(z)\).
In vicinity of the real axis, the Doya function and its itetates can be expressed through the LambertW function as follows:
- \(\displaystyle \!\!\!\!\!\!\!\!\!\!\! (11) ~ ~ ~ \mathrm{Doya}^t(z)=\mathrm{LambertW}( z \exp(z\!+\!t))\)
Expansion at small values of the argument can be written as follows:
- \(\displaystyle \!\!\!\!\!\!\!\!\!\!\!\!\! (12) ~ ~ ~ \mathrm{Doya}^t(z)= e^t z-e^t \left(e^t-1\right) z^2\) \( +\frac{1}{2} e^t \left(-4 e^t+3 e^{2 t}+1\right) z^3\) \( -\frac{1}{6} e^t \left(12 e^t-27 e^{2 t}+16 e^{3 t}-1\right) z^4\) \( +O\left(z^5\right)\)
Expansion at large values of the argument can be written as follows:
- \(\displaystyle \!\!\!\!\!\!\!\!\!\!\!\!\! (13) ~ ~ ~ \mathrm{Doya}^t(z)= z +t\) \( - t z^{-1}\) \( +\frac{t (t+2)}{2} z^{-2}\) \( -\frac{t \left(2 t^2+9 t+6\right)}{6} z^{-3}\) \( +~\Big(\frac{t^4}{4}+\frac{11 t^3}{6}+3 t^2+t \Big) z^{-4}\) \( +~O(z^{-5}) \)
Expansion at small value of the parameter:
- \(\displaystyle \!\!\!\!\!\!\!\!\!\!\!\!\! (14) ~ ~ ~ \mathrm{Doya}^t(z)= z +\frac{t z}{z+1}\) \( +\frac{t^2 z}{2 (z+1)^3} \) \( +\frac{t^3 z (1-2 z)}{6 (z+1)^5} \) \( +\frac{t^4 z (6 z^2-8 z+1)}{24 (z+1)^7}\) \( +O(t^5) \)
Implementation of the Doya function
In principle, with the properties above, the Doya function could be implemented as the appropriate combination of the truncated series. However, the implementation through the Tania function is simpler. This implementation is suggested at the file doya.cin. It is implemented as complex[double) function of two complex(double) parameters. the first of them transfers the value of parameter, denoted with \(t\) above; the second is just argument denoted with \(z\) above.
The correct treating of the complex argument is essential for the uniqueness of the function. For example, the two different super–exponentials, constructed at two different fixed points, may coincide along the real axis with 24 decimal digits [1], and the high precision arithmetic is necessary to see the difference while working with real numbers. However, the difference become clearly seen is these functions are plotted in the complex plane. In such a way, the tests of this function for complex values of argument gives the hope, that "the true and the only" transfer function is implemented.
The similar function can be implemented through the LambertW function (called also "ProductLog"), at the real axis such an implementation should give the same values as the doya.cin does. The function is supposed to return of order of 14 correct decimal digits; but if any peculiarities at the use, the feedback should be greatly appreciated.
Application of the Doya function
Scientific application
In the simple model of a nonlinear amplifier, the transfer function can be expressed in terms of the Doya function as follows:
- \( \displaystyle \!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\! (15) ~ ~ ~ T(z)= P_{\rm sat} \mathrm{Doya}_t(z/P_{\rm sat})\)
where \(P_{\rm sat}\) is the saturation power; roughly the product of \(I_{\rm sat}\) and the area of cross-section of the active region. In this case, \(t\) has sense of the unsaturated at the length of the amplifier. In that model, the transfer function is determined by the two parameters \(P_{\rm sat}\) and \(t\) through the known functions Doya and Tania. Such a model seems to be applied, in particular, for the Yb-doped laser materials; realistic values for the saturation intensity can be of order of a hundred Watt/cm\(^2\) [2]; at the transversal size of active zone of order of a hundred micron, the saturation power \(P_{\rm sat}\) is of order of one watt. The unsaturated gain \(t\) can be of order of unity or smaller for the crystal lasers or ceramic lasers (and much smaller than unity for the powerful disk lasers [3]) and much larger than unity for the fiber disk lasers [4]. However, at the optimization of the performance of the device, the realization usually gets out from the limits of applicability of a simple model; for this reason, the approximation of transfer function of the commercial laser amplifier with the Doya function is expected to give only qualitative agreement with the actual characteristics of the device. The comparison to the experiments (and setting limits of applicability of the simplest model) may be good topic for the scientific research.
In physical experiments, it is much easier to measure the transfer function of an optical fiber than to trace the evolution of the power of the amplified light along its propagation. For this reason, the Doya function is expected to be useful tool in the laser science.
Keller function
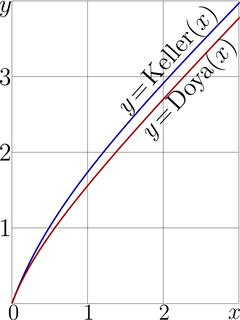
The Doya function describes the amplification of a continuous waves in a laser medium with unsaturated gain unity, id est, with coefficient of amplivication of small signal equal to the base of natural logarithm; the simple two–level model for the kinetics of the excitations is used. In this case, the argument of the Doya function is intensity at the input, normalized for the saturation intensity.
Similar transfer function can be obtained within the same model for the amplification of short pulses; on TORI, it is called Keller function. The argument of this function may have sense of the input fluence of the amplifier; and the returned value corresponds to the output fluence in the same units. The Keller function can be expressed through the exponential and logarithm as follows:
- \( \displaystyle \!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\! (16) ~ ~ ~ \mathrm{Keller}(z)=z+\ln\!\Big(\mathrm e - \mathrm e^{-z}(\mathrm e-1) \Big)\)
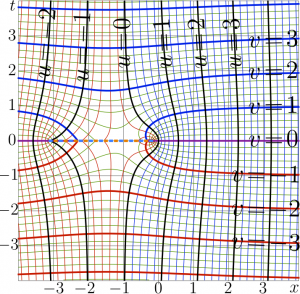
Figure at right shows the comparison of the Keller function to the Doya function.
Up to beginning of century 21, the quality of measurement of the transfer functions for the samples of the nonlinear optical materials is not high. Looking at the experimental data, it is difficult to guess, which function would better fit the dots, the Doya function or the Keller function, id est, to distinguish the case of amplification of the continuous wave (when the intensity is normalized for the saturation intensity) from the case of short pulses (when the fluence is normalized for the saturation fluence); the curves at teh figure look similar.
"Recovery" of Tania function from Doya function
The representation of Doya function through the Tania function is explicit. However, the experimental situation is opposite: one can measure the transfer function and try to recover the superfunction [5]. This situation is modeled in this section. The Regular iteration is applied to the Doya function in order to show that it leads to the Tania function.
The transfer equation has form
- \( \displaystyle \!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\! (16) ~ ~ ~ \mathrm{Doya_t}(\mathrm{Tania}(x))=\mathrm{Tania}(x\!+\!1)\)
Following the general case of the Regular iteration, search the solution \(P\) in the following form:
- \(\displaystyle \!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\! (17) ~ ~ ~ P(x)=\varepsilon+ a_2 \varepsilon^2 + a_3 \varepsilon^3 + ...\)
where \(\varepsilon=\exp(kx)\); \(k\) and coefficients \(a\) are parameters that might depend on \(t\), but not on \(x\). This \(\varepsilon\) appears as small parameter at the expansion of the superfunction at larhe negative values of the argument. Then, \(P(x\!+\!1)\) can be expressed as follows:
- \( \displaystyle \!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\! (18) ~ ~ ~ P(x\!+\!1)=k \varepsilon + k^2 a_2 \varepsilon^2 + k^3 a_3 \varepsilon^3 + ...\)
The substitution of the series to the Transfer Equation gives value of increment \(k=\exp(t)\) and the coefficients \(a_2\!=\!-1\), \(a_3\!=\!3/2\), etc.. The iteration of the transfer equation allows the evaluation of Tania function at least along the real axis.
The expansion of \(P\) agrees with (8); at \(t\!=\!1\), the condition \(\mathrm{Tania}(0)\!=\!1\) allows to express Tania as
- \( \mathrm{Tania}(x)=P(x\!+\!1)\)
The asymptotic agreement gives hopes to have agreement also with the experimental data; the measured transfer functions for the optical systems should be greatly appreciated.
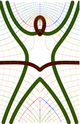
Artistic application
According to eq.(11), at large values of the argument, the Doya function behaces in a way, similar to its argument. The compex map can be used in the artistic works. The example is shown in the figure at right. The levels \(\Im(\mathrm{Doya}_1(y\!+\!{\rm i} x)=\pm 1.2\) and \(\Im(\mathrm{Doya}_1(y\!+\!{\rm i} x)=\pm 1.4\) and \(\Re(\mathrm{Doya}_1(y\!+\!{\rm i} x)=\pm -0.4\) are shown with thick lines. This image is used in the article Science.
About the name of the function
The Doya function is named after Valérie Doya [6], who works in the University of Nice, together with Olivier Legrand, Fabrice Mortessagne and other colleagues. In 2008 June, the joint attempt to apply the superfunctions to the physical research took place. That time, it was not recognized that formalism of superfunctions [7][8][9][10][1][11][12] should be carefully built-up first; and this took several years [13] needs few years of research, instead of one month, as it was planned in 2008, before the application.
Conclusion
The Doya function of a single variable with a single additional parameter is introduced to describe the transfer function of the laser amplifiers within the simple model of the laser kinetics. The transfer function of a realistic device is suggested to be approximated by expression (21) with two parameters: unsaturated gain \(t\) and the saturation power \(P_{\rm sat}\). The comparison of such approximation to the experimental measurements should be greatly appreciated.
Keywords
LambertW function, Laser science, Superfunction, Tania function, Transfer equation, Transfer function
References
- ↑ 1.0 1.1 http://www.ams.org/journals/mcom/2010-79-271/S0025-5718-10-02342-2/home.html D.Kouznetsov, H.Trappmann. Portrait of the four regular super-exponentials to base sqrt(2). Mathematics of Computation, 2010, v.79, p.1727-1756.
- ↑ http://tori.ils.uec.ac.jp/PAPERS/2005josab.pdf D.Kouznetsov, J.-F.Bisson, K.Takaichi, K.Ueda. High-power single-mode solid-state laser with a short, wide unstable cavity. JOSA B, v.22, Issue 8, p.1605-1619 (2005).
- ↑ http://www.ils.uec.ac.jp/~dima/PAPERS/2009optmat.pdf D.Kouznetsov, J.-F.Bisson, K.Ueda. Scaling laws of disk lasers. Optical Materials, 31 (2009) 754–759.
- ↑ http://en.wikipedia.org/wiki/Fiber_disk_laser
- ↑ http://tori.ils.uec.ac.jp/PAPERS/2011singapo.pdf D.Kouznetsov. Transfer function of an amplifier and characterization of Materials. Singapore, 2011.
- ↑ http://valerie.doya.free.fr/Doya_CV.html Valérie DOYA. Doctor in Physics. Researcher and teacher at the University of Nice. (2004)
- ↑ http://www.ams.org/mcom/2009-78-267/S0025-5718-09-02188-7/home.html D.Kouznetsov. Solutions of F(z+1)=exp(F(z)) in the complex zplane. Mathematics of Computation, 78 p.1647-1670 (2009)
- ↑ http://www.ils.uec.ac.jp/~dima/PAPERS/2009supefae.pdf D.Kouznetsov, H.Trappmann. Superfunctions and square root of factorial. Moscow University Physics Bulletin, 2010, v.65, No.1, p.6-12.
- ↑ http://www.springerlink.com/content/u712vtp4122544x4 D.Kouznetsov. Holomorphic extension of the logistic sequence. Moscow University Physics Bulletin, 2010, No.2, p.91-98. (Russian version: p.24-31)
- ↑ http://tori.ils.uec.ac.jp/PAPERS/2010vladie.pdf D.Kouznetsov. Superexponential as special function. Vladikavkaz Mathematical Journal, 2010, v.12, issue 2, p.31-45.
- ↑
http://tori.ils.uec.ac.jp/PAPERS/2012e1eMcom2590.pdf and/or
http://tori.ils.uec.ac.jp/PAPERS/2011e1e.pdf H.Trappmann, D.Kouznetsov. Computation of the Two Regular Super-Exponentials to base exp(1/e). Mathematics of Computation. Math. Comp., v.81 (2012), p. 2207-2227. - ↑ http://www.springerlink.com/content/u7327836m2850246/ H.Trappmann, D.Kouznetsov. Uniqueness of Analytic Abel Functions in Absence of a Real Fixed Point. Aequationes Mathematicae, v.81, p.65-76 (2011)
- ↑
http://link.springer.com/article/10.1007/s10043-013-0058-6
http://mizugadro.mydns.jp/PAPERS/2013or1.pdf single column version dor reading
http://mizugadro.mydns.jp/PAPERS/2013or2.pdf two column version for printing
D.Kouznetsov. Superfunctions for amplifiers. Optical Review, July 2013, Volume 20, Issue 4, pp 321-326.
http://www.rp-photonics.com/gain_saturation.html Gain Saturation
