AuNem

\(q\!=\!0\), \(q\!=\!1\) and \(q\!=\!2\)]]



AuNem is Abel function of the Nemtsov function, \(\mathrm{Nem}_q(z)=z+z^3+q z^4 ~ ~\), where \(q~\) is positive parameter.
Limiting case \(q\!\rightarrow\!0\) also can be considered.
Value of \(q\) can be indicated as subscript after the name of the function.
AuNem is inverse function of function SuNem;
\(\mathrm{SuNem}_q(\mathrm{AuNem}_q(z))=z\)
\(G=\mathrm{Nem}_q\) is solution of the Abel equation for the transfer function \(T=\mathrm{Nem}_q\) :
\(G(T(z))=G(z)+1\)
For real values of the argument, explicit plot of AuNem is shown in Fig.1; \(y\!=\!\mathrm{AuNem}_q(z)~\) is drawn versus \(x\) for \(q\!=\!0\), \(q\!=\!1\) and \(q\!=\!2\).
For \(q\!=\!0\), \(q\!=\!1\) and \(q\!=\!2\), complex map of function \(\mathrm{AuNem}_q\) is shown in figures 2,3,4.
Asymptotic behaviour of AuNem
The asymptotix behaviour of AuNem at small valies of the argiment (at least for positive argument) is determined by the asymptotic behaviour of function SuNem at large negative values of the real part of the argument. Inverting the corresponding expansion for SuNem, the asymptic can be written as follows. For some positive integer \(M\), let
\(\mathrm{AuNe}_{q,M}(z)= \) \( \displaystyle -\frac{1}{2 z^2}+\frac{q}{z}\) \( \displaystyle +\frac{1}{2} \left(2 q^2+3\right) \log (z)\) \( \displaystyle +\frac{q^2}{2}+\frac{1}{4} \left(2 q^2+3\right) \log (2)\) \( \displaystyle +\sum _{n=1}^M c(n) z^n \)
\(\mathrm{AuNem}_{q}(z)=\mathrm{AuNem}_{q,M}(z) +O(z^{M+1})\)
Coefficients \(c\) can be found from the asymptotic analysis of equation \(\mathrm{SuNem}_q(\mathrm{AuNem}(z))=0\). The coefficients can be deduced also from the Abel equation; in this case, some tens of coefficients can be evaluated with the Mathematica. The mathematica code is copypasted below:
T[z_] = z + z^3 + q z^4
P[m_, L_] := Sum[a[m, n] L^n, {n, 0, IntegerPart[m/2]}]
F[m_, z_] := 1/(-2 z)^(1/2) (1 - q/(-2 z)^(1/2) + Sum[P[n, Log[-z]]/(-2 z)^(n/2), {n,2,m}])
G[m_, x_] := -1/(2 x^2) + q/x + q^2/2 + 1/4 (3 + 2 q^2) Log[2] + 1/2 (3 + 2 q^2) Log[x] + Sum[c[n] x^n, {n,1,m}]
Series[ReplaceAll[F[3, h + G[3, z]], a[2, 1] -> 1/4 (3 + 2 q^2)], {z,0,4}]
m = 1; sg[m] = Coefficient[Series[G[m + 3, T[z]] - G[m + 3, z] - 1, {z,0,3}], z^(m + 2)]
st[m] = Solve[sg[m] == 0, c[m]]
su[m] = Extract[st[m], 1]
SU[m] = su[m];
m = 2;
sf[m] = Series[ ReplaceAll[G[m + 3, T[z]] - G[m + 3, z] - 1, SU[m-1]], {z,0,m+2}]
sg[m] = Simplify[Coefficient[sf[m] 2^m, z^4]]
st[m] = Solve[sg[m] == 0, c[m]]
SU[m] = Join[SU[m - 1], su[m]]
m = 3;
sf[m] = Series[ ReplaceAll[G[m + 3, T[z]] - G[m + 3, z] - 1, SU[m-1]], {z,0,m+2}]
sg[m] = Simplify[Coefficient[sf[m] 2^m, z^(m+2)]]
st[m] = Solve[sg[m] == 0, c[m]]
su[m] = Extract[st[m], 1]
SU[m] = Join[SU[m-1], su[m]]
(*and so on.. *)
After to accumulate 40 substitutions in variable SU, the C++ code for evaluation of the truncated asymptotic can be generated with the command below:
For[m=1,m<41, Print["C[", m, "]=", CForm[ReplaceAll[HornerForm[ReplaceAll[c[m],SU[m]]], {q^2->K, q->Q}]], ";"]; m++;]
The resulting output is stored in file aunemco.txt; this file is used at the C++ implementation of function AuNem. Values of \(q\) and \(q^2\) should be stored in the global variables Q and K.
Extension to the whole complex plane
The asymptotic expansion of function AuNem above is valid only for the small part of vicinity of the positive part of the real axis, while the argument is small.
This representation can be extended, using the inverse function of the Nemtsov function; this inverse function is denoted as ArqNem. It is important to use namely ArqNem, while two other inverse functions, ArcNem and ArkNem do not provide the convergence of the iterative procedure below.
For some fixed integer \(M\!>\!0\), the Abel function \(G=\mathrm{AuNem}_q=\mathrm{SuNem}_q^{-1}\) appears as limit:
\(\displaystyle G(z)=\lim_{n\rightarrow \infty} \Big(G_M(\mathrm{ArqNem}^n(z))+n\Big)\)
where
\(G_{M}(z)=\) \( \displaystyle -\frac{1}{2 z^2}+\frac{q}{z} +\frac{1}{2} \left(2 q^2+3\right) \log (z) +\frac{q^2}{2}+\frac{1}{4} \left(2 q^2+3\right) \log (2)\) \( \displaystyle +\sum _{n=1}^M c(n) z^n \)
The limit does not depend on \(M\), although, for higher \(M\), the rate of convergence is higher. Practically, at \(M\!=\!40\), to get at least 14 decimal digits, it is sufficient to use the approximation of limit with \(n\!=\!10\); id est, the complex double implementation evaluates function ArqNem 20 times, and once evaluates the approximation \(G\) above.
As function \(\mathrm{AuNe}_q\) is defined, the inverse of the superfunction SuNem appears as follows:
\(\mathrm{AuNem}_q(z)=\mathrm{AuNe}_q(z)-\mathrm{AuNe}_q(1)\)
Such a definition automatically provides the relation \(\mathrm{AuNem}_q(1)=0\), as it is supposed to while \(\mathrm{SuNem}(0)\!=\!1\).
The precision of the implementation of function AuNem can be verified by evaluation of the agreement
\(\displaystyle A_{\mathrm{inver}}(z)= -\lg\left(\frac {|\mathrm{SuNem}_q(\mathrm{AuNem}_q(z))-z|} {|\mathrm{SuNem}_q(\mathrm{AuNem}_q(z))|+|z|} \right) \)
with function SuNem, and also by the substituiton into the Abel equation and evaluation of agreement
\(\displaystyle A_{\mathrm{abel}}(z)= -\lg\left(\frac {|\mathrm{AuNem}_q(\mathrm{Nem}_q(z))-(\mathrm{AuNem}_q(z)\!+\!1)|} {|\mathrm{AuNem}_q(\mathrm{Nem}_q(z))|+|\mathrm{AuNem}_q(z)\!+\!1|} \right)\)
Roughly, these agreements indicate, how many decimal digits can one expect to get at the numerical implementation. The numerical implementations used to plot figures provide of order of 14 significant figures; this is close to the maximal precision reachable with the complex double variables.
Branch points and the cut lines
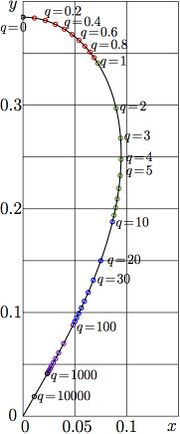
The definition of AuNem and its representation above are used to plot figure 1 and to make the complex maps in figures 2,3,4. In these figures, the additional grid lines are adder, that correspond to \(x\!=\!x_0\) and to \(y\!=\!\pm y_0\) such that \(x_0\!+\!\mathrm i y_0\) is branch point of function ArqNem; it is also branch point of function AuNem. Definition of function AuNem indicates, that its branch points and the cut lines coincide with those of function ArqNem.
Values of \(x_0\) and \(y_0\) are determined by parameter \(q\) through function NemBran:
\(x_0\!+\!y_0 = \mathrm{NemBran}(q)\)
Parametric plot \(x+\mathrm i y= \mathrm{NemBran}(q)\) is shown in figure 5 for real valies of \(q\) from zero to infinity.
Note, that at increment of value of function AuNem or, that is equivalent, at modification of its argument with function AuNem, its argument becomes farther from the cut lines, except values at vicinity of the real axis. This means, that at iterates of function ArqNem, the argument of AuNem gradual approaches to range of validity of the asymptotic approximation, until the approximation provides the required precision. In the figures, the routines are used that provide of order of 14 significant figures, that greatly exceed the precision, required for the camera–ready versions of the figures, but some extra digits are useful for the numerical, computational test of performance of the C++ implementations, mapping the agreements \(A_{\mathrm{inverse}}(x\!+\!\mathrm i y)\) and \(A_{\mathrm{Abel}}(x\!+\!\mathrm i y)\) in the \(x\), \(y\) plane.
Such a phenomenon did not happen by itself; it is due to the special choice of the cut lines of function ArqNem. Other inverse functions for the Nemtsov function do not provide this property and, therefore, cannot be used for approximation of AuNem in the whole complex plane. However, they can be used too for evaluation of function AuNem in vicinity of the real axis, where values of functions ArqNem, Arknem and ArcNem coincide.
Iterates of the Nemtsov function
Functions \(F\!=\!\mathrm{SuNem}_q\) and \(G\!=\!\mathrm{AuNem}_q\) are Superfunction and Abel function for the Nemtsov function \(\mathrm{Nem}_q\).
Iterates of the Nemtsov function can be expressed through functions SuNem and AuNem
\(\mathrm{Nem}_q^{~n}=F(n+G(z))\)
In this representation, the number \(n\) of iterates has no need to be integer.
References
Keywords
Abel function, ArqNem, Book, Exotic iterate, Iterate, Nemtsov function, SuNem, Superfunctions