File:FactoriAsymptoAgreeT.png
Original file (800 × 667 pixels, file size: 51 KB, MIME type: image/png)
Summary
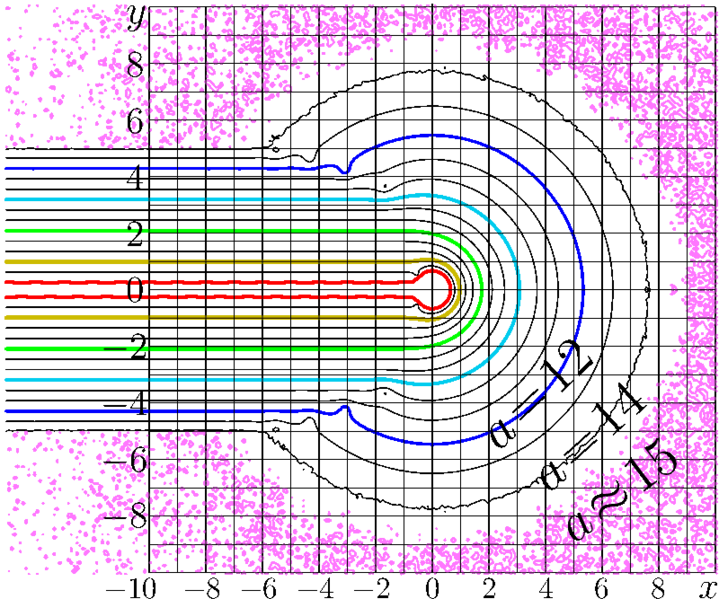
Map of agreement \[ a(z) = - \lg \left(\frac {|z!-A(z)|} {|z!|+|A(z)|} \right) \] of the asymptotic \[ A(z)= \sqrt{2\pi z}\ \exp\left(\log\left(\frac{z}{\mathrm e} \right) z + \frac{1}{12 z}\left(1+ \frac{1}{z^2}\left(\frac{-1}{30}+ \frac{1}{z^2}\left(\frac{1}{105}+ \frac{1}{z^2}\left(\frac{-1}{140}+ \frac{1}{z^2}\left(\frac{1}{99}+ \frac{1}{z^2}\left(\frac{-1}{42} \right) \right) \right) \right) \right) \right) \right) \] with function Factorial \( z \mapsto z!\).
The agreement \(a=a(x\!+\!\mathrm i y)\) is shown with levels \(a=\mathrm{const}\) in the \(x,y\) plane
Levels \(a\!=\!1\), \(a\!=\!3\), \(a\!=\!6\), \(a\!=\!9\), \(a\!=\!12\) are appear as thick colored curves.
The pink shade is an attempt to draw level \(a\!=\!15\). Apparently, the rounding errors of the complex double variables do not allow to draw the smooth contour - at least with the current implementation fac.cin of the Factorial function. (Is someone can do it better, go ahead!)
The picture is prepared as an example for articles «Asymptotic», «Restricted asymptotic», «Sectorial asymptotic».
Also, the map serves as test for routines Conrec6.cin and fac.cin; the code below can be used as an example of the driver routine (program that calls the routine(s)).
Interpretation
The map suggests that the asymptotic \(A(z)\) above returns at least 14 significant figures of Factorial\((z)\) in the range \[ d = (\ \Re(z) \!\ge\! -6 , \ |z|\!>\!8\ )\ \lor \ (\Re(z)\!<\!-6 , \ |\Im(z)|\!>\!5 \ ) \]
Function \(A\) is interpreted as Restricted asymptotic:
It is the Sectorial asymptotic of Factorial at large values of its argument for sector \[ D= \{ z\in \mathbf C \ : |\arg(z)|< \alpha \} \] where \(\alpha\) is any positive real number such that \( \alpha < \pi \).
At large \(|z|\), the residual \(r(z)=\)Factorial\((z) - A(z) \) remains small compared to Factorial\((z)\) in the whole complex \(z\) plane except arbitrary narrow sector the includes the negative part of the real axis: \[ \lim_{|z|\to \infty, \ z \in D} \frac{r(z)}{z!} = 0 \]
C++
/* Routines
«ado.cin»,
«Conrec6.cin»,
«fac.cin»
should be loaded for the compilation of the code below.
Options « -std=c++11 -O2 » are strongly recommended. */
// c++ -std=c++11 FactoriAsymptoAgree.cc -O2 -o FactoriAsymptoAgree
#include <math.h>
#include <stdio.h>
#include <stdlib.h>
#define DB double
#define DO(x,y) for(x=0;x<y;x++)
using namespace std;
#include <complex>
typedef complex<double> z_type;
#define Re(x) x.real()
#define Im(x) x.imag()
#define I z_type(0.,1.)
#include"ado.cin"
#define M(x,y) fprintf(o,"%6.4f %6.4f M\n",1.*(x),1.*(y));
#define L(x,y) fprintf(o,"%6.4f %6.4f L\n",1.*(x),1.*(y));
#include "Conrec6.cin"
#include "fac.cin"
z_type facas(z_type z){ z_type c=1./z; z_type d=c*c;
return sqrt(M_PI*2.*z)*exp(log(z/M_E)*z+(1./12.)*c*(
1.+d*(-1./30.+d*(1./105.+d*(-1./140.+d*(1./99.+d*(-1./42.)))))
));
//(1.+c*(1./12.+c*(1./288.+c*(-139./51840.))));
}
int main(){ int j,k,m,n; DB x,y, p,q, t; z_type z,c,d;
int M=251,M1=M+1;
int N=201,N1=N+1;
DB X[M1],Y[N1], g[M1*N1];
//,f[M1*N1];
FILE *o;o=fopen("FactoriAsymptoAgree.eps","w");ado(o,252,202);
fprintf(o,"151 101 translate\n 10 10 scale\n");
DO(m,M1) X[m]=-15+.1*(m-.5);
DO(n,N1) Y[n]=-10+.1*(n-.5);
DO(m,M1)DO(n,N1){g[m+M1*n]=9999;}
DO(m,M1){x=X[m]; //printf("%5.2f\n",x);
DO(n,N1){y=Y[n]; z=z_type(x,y);
// c=Filog(z);
//c=z*z*sin(1./z);
c=fac(z);
d=facas(z);
p= - log( abs(c-d) / (abs(c)+abs(d)) )/log(10.);
//p=Re(c);q=Im(c);
g[m+M1*n]=p;
}}
fprintf(o,"1 setlinejoin 1 setlinecap\n"); p=5.;q=1;
p=15.;
Conrec6(o,g,X,Y,M1,N1, 1. ,p); fprintf(o,".12 W 1 0 0 RGB S\n");
Conrec6(o,g,X,Y,M1,N1, 2. ,p); fprintf(o,".04 W 0 0 0 RGB S\n");
Conrec6(o,g,X,Y,M1,N1, 3. ,p); fprintf(o,".12 W .6 .4 0 RGB S\n");
Conrec6(o,g,X,Y,M1,N1, 4. ,p); fprintf(o,".06 W 0 0 0 RGB S\n");
Conrec6(o,g,X,Y,M1,N1, 5. ,p); fprintf(o,".06 W 0 0 0 RGB S\n");
Conrec6(o,g,X,Y,M1,N1, 6. ,p); fprintf(o,".12 W 0 .8 0 RGB S\n");
Conrec6(o,g,X,Y,M1,N1, 7. ,p); fprintf(o,".06 W 0 0 0 RGB S\n");
Conrec6(o,g,X,Y,M1,N1, 8. ,p); fprintf(o,".06 W 0 0 0 RGB S\n");
Conrec6(o,g,X,Y,M1,N1, 9. ,p); fprintf(o,".12 W 0 .5 .6 RGB S\n");
Conrec6(o,g,X,Y,M1,N1, 10. ,p); fprintf(o,".06 W 0 0 0 RGB S\n");
Conrec6(o,g,X,Y,M1,N1, 11. ,p); fprintf(o,".06 W 0 0 0 RGB S\n");
Conrec6(o,g,X,Y,M1,N1, 12. ,p); fprintf(o,".12 W 0 0 1 RGB S\n");
Conrec6(o,g,X,Y,M1,N1, 13. ,p); fprintf(o,".06 W 0 0 0 RGB S\n");
Conrec6(o,g,X,Y,M1,N1, 14. ,p); fprintf(o,".06 W 0 0 0 RGB S\n");
Conrec6(o,g,X,Y,M1,N1, 15. ,p); fprintf(o,".07 W 1 .5 1 RGB S\n");
for(m=-10;m<11;m++){if(m!=0){M(m,-10)L(m,10)}}
for(n=-10;n<11;n++){M(-10,n)L(10,n)}
fprintf(o,"2 setlinecap .02 W 0 0 0 RGB S\n");
fprintf(o,"2 setlinecap .02 W 0 0 0 RGB S\n");
M(0,-10)L(0,11)
fprintf(o,"2 setlinecap .03 W 0 0 0 RGB S\n");
fprintf(o,"showpage\n%c%cTrailer",'%','%'); fclose(o);
system("epstopdf FactoriAsymptoAgree.eps");
system( "open FactoriAsymptoAgree.pdf"); //for mac
}
Latex
%I have no idea why I have to declare paper
%sizes 803x669 in order to get picture of
%sizes 800x667
\documentclass[12pt]{article}
\usepackage{geometry}
\paperwidth 803pt
\paperheight 669pt
\textwidth 800pt
\textheight 700pt
\topmargin -106pt
\oddsidemargin -116pt
\usepackage{graphicx}
\usepackage{rotating}
\newcommand \rot {\begin{rotate}}
\newcommand \ero {\end{rotate}}
\newcommand \rme {\mathrm{e}}
\newcommand \sx {\scalebox}
\begin{document}
\sx{3.15}{\begin{picture}(230,211)
\normalsize
%\put(40,0){\ing{oblakoV}}
%\put(10,10){\includegraphics{Z2sin1zMap}}
\put(10,8){\includegraphics{FactoriAsymptoAgree}}
\put(53,204){\sx{1.2}{\(y\)}}
\put(53,185){\sx{1.1}{\(8\)}}
\put(53,165){\sx{1.1}{\(6\)}}
\put(53,145){\sx{1.1}{\(4\)}}
\put(53,125){\sx{1.1}{\(2\)}}
\put(53,105){\sx{1.1}{\(0\)}}
\put(44,85){\sx{1.1}{\(-2\)}}
\put(44,65){\sx{1.1}{\(-4\)}}
\put(44,45){\sx{1.1}{\(-6\)}}
\put(44,25){\sx{1.1}{\(-8\)}}
\put(45, 0){\sx{.9}{\(-10\)}}
\put(73, 0){\sx{.9}{\(-8\)}}
\put(93, 0){\sx{.9}{\(-6\)}}
\put(113, 0){\sx{.9}{\(-4\)}}
\put(133, 0){\sx{.9}{\(-2\)}}
\put(159, 0){\sx{.9}{\(0\)}}
\put(179, 0){\sx{.9}{\(2\)}}
\put(199, 0){\sx{.9}{\(4\)}}
\put(219, 0){\sx{.9}{\(6\)}}
\put(239, 0){\sx{.9}{\(8\)}}
\put(256, 0){\sx{1.1}{\(x\)}}
%\put(8,194){\sx{1.4}{\rot{0}\(a\!\approx\!15\) \ero} }
%\put(132,196){\sx{1.6}{\rot{0}\(a\!\approx\!15\) \ero} }
%\put(132,176){\sx{1.6}{\rot{0}\(a\!=\!14\) \ero} }
%\put(132,156){\sx{1.6}{\rot{0}\(a\!=\!12\) \ero} }
\put(185,52){\sx{1.6}{\rot{42}\(a\!=\!12\) \ero} }
\put(203,37){\sx{1.6}{\rot{40}\(a\!=\!14\) \ero} }
\put(212,19){\sx{1.6}{\rot{37}\(a\!\approx\!15\) \ero} }
\end{picture}}
\end{document}
Acknowledgement
Routine Conrec6.cin is used to draw lines.
This routine is tailored in collaboration with ChatGPT.
Please attribute the source at the reuse:
the attribution helps to trace bug(s) if any.
The picture generated with the C++ and the Latex above is converted to PNG with command
convert FactoriAsymptoAgreeT.pdf png8:FactoriAsymptoAgreeT.png
References
https://en.wikipedia.org/wiki/Stirling%27s_approximation In mathematics, Stirling's approximation (or Stirling's formula) is an asymptotic approximation for factorials. ..
Keywords
«[[]]», «Agreement», «Asymptotic», «ChatGPT», «ado.cin», «Conrec6.cin», «fac.cin» «Factorial», «Map», «Restricted asymptotic», «Sectorial asymptotic», «Stirling»,
File history
Click on a date/time to view the file as it appeared at that time.
| Date/Time | Thumbnail | Dimensions | User | Comment | |
|---|---|---|---|---|---|
| current | 19:48, 19 January 2026 |  | 800 × 667 (51 KB) | T (talk | contribs) | misprint in the code had been corrected |
| 18:36, 18 January 2026 |  | 800 × 667 (50 KB) | T (talk | contribs) | {{oq|FactoriAsymptoAgreeT.png|Original file (800 × 667 pixels, file size: 50 KB, MIME type: image/png)|400}} Map of agreement \[ a(z) = - \lg \left(\frac {|z!-A(z)|} {|z!|+|A(z)|} \right) \] of the asymptotic \[ A(z)= \sqrt{2\pi z}\ \exp\left(\log\left(\frac{z}{\mathrm e} \right) z + \frac{1}{12 z}\left(1+ \frac{1}{z^2}\left(\frac{-1}{30}+ \frac{1}{z^2}\left(\frac{1}{105}+ \frac{1}{z^2}\left(\frac{-1}{140}+ \frac{1}{z^2}\left(\frac{1}{99}+ \frac{1}{z^2}\left(\frac{-1}{42} \right) \rig... |
You cannot overwrite this file.
File usage
The following page uses this file: