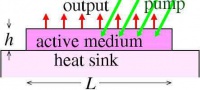
Active mirror
A disk laser or active mirror (Fig.1.) is a type of solid-state laser characterized by a heat sink and laser output that are realized on opposite sides of a thin layer of active gain medium.[1].
Terminology
Historically, the term "Active mirror" was used; in century 21, the term "disk laser" seems to be more usual. Despite their name, disk lasers do not have to be circular; other shapes have also been tried. In TORI, the term "Active mirror" is used, because the term "disk laser" is easy to confuse with Laserdisc, which is a disk-shaped optical storage medium.
Initially, disk lasers were called active mirrors, because the gain medium of a disk laser is essentially an optical mirror with reflection coefficient greater than unity. An active mirror is a thin disk-shaped double-pass optical amplifier.
The first active mirrors were developed in the Laboratory for Laser Energetics (USA).[3] Then, the concept was developed in various research groups, in particular, the University of Stuttgart (Germany)[4] for Yb:doped glasses.
In the disk laser, the heat sink does not have to be transparent, so, it can be extremely efficient even with large transverse size \(~L~\) of the device (Fig.1.). The increase in size allows the power scaling to many kilowatts without significant modification of the design.[5]
Limit of power scaling for disk lasers
The power of such lasers is limited not only by the power of pump available, but also by overheating, amplified spontaneous emission (ASE) and the background round-trip loss.[6] To avoid overheating, the size \(~L~\) should be increased with power scaling. Then, to avoid strong losses due to the exponential growth of the ASE, the transverse-trip gain \(~u=GL~\) cannot be large. This requires reduction of the gain \(G~\); this gain is determined by the reflectivity of the output coupler and thickness \(~h\). The round-trip gain \(~g=2Gh~\) should remain larger than the round-trip loss \(\beta~\) (the difference \(g\!-\!\beta~\) determines the optical energy, which is output from the laser cavity at each round-trip). The reduction of gain \(G~\), in a given round-trip loss \(~\beta~\), requires increasing the thickness \(h\). Then, at some critical size, the disk becomes too thick and cannot be pumped above the threshold without overheating.
Some features of the power scaling can revealed from a simple model. Let \(Q~\) be the saturation intensity,[7] [6] of the medium, \(\eta_0=\omega_{\rm s}/\omega_{\rm p}~~\) be the ratio of frequencies, \(R~\) be the thermal loading parameter. The key parameter \(P_{\rm k}=\eta_0\frac{R^2}{Q\beta^3}~\) determines the maximal power of the disk laser. The corresponding optimal thickness can be estimated with \(h \sim \frac{R}{Q \beta}\). The corresponding optimal size \(L \sim \frac{R}{Q \beta^2}\). Roughly, the round-trip loss should scale inversely proportionally to the cubic root of the power required.
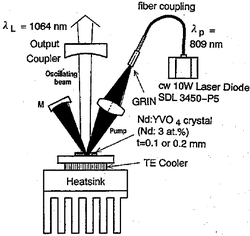
An additional issue is the efficient delivery of pump energy. In low round-trip gain, the single-pass absorption of the pump is also low. Therefore, recycling of pump energy is required for efficient operation. (See the additional mirror M at the left-hand side of figure 2.) For power scaling, the medium should be optically thin, with many passes of pump energy required; the lateral delivery of pump energy [7] also might be a possible solution.
Anti-ASE cap
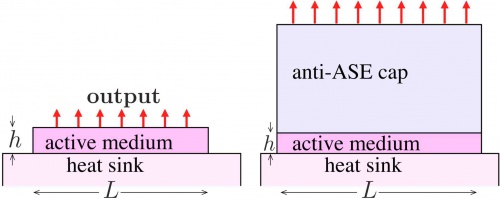
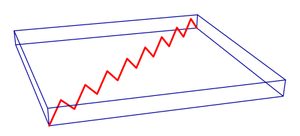
In order to reduce the impact of ASE, an anti-ASE cap consisting of undoped material on the surface of a disk laser has been suggested.[9][10] Such a cap allows spontaneously emitted photons to escape from the active layer and prevents them from resonating in the cavity. Rays cannot bounce (Fig.3) as in uncovered disk. This could allow an order of magnitude increase in the maximum power achievable by a disk laser .[8] In both cases, the back reflection of the ASE from the edges of the disk should be suppressed. This can be done with absorbing layers, shown with green in Figure 4. At operation close to the maximal power, a significant part of the energy goes into ASE; therefore, the absorbing layers also should be supplied with heat sinks, which are not shown in the figure.
Key parameter for laser materials
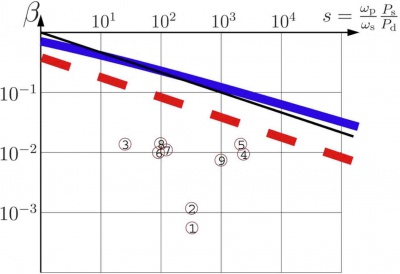
The estimate of maximal power achievable at given loss \(\beta\), is very sensitive to \(\beta\). The estimate of the upper bound of \(\beta\), at which the desired output power \(P_{\rm s}\) is achievable is robust. This estimate is plotted versus normalized power \(s=P_{\rm s}/P_{\rm d}\) in figure 5. Here, \( P_{\rm s}\) is the output power of the laser, and \(P_{\rm d}=R^2/Q\) is dimensional scale of power; it is related with the key parameter \(P_{\rm k}=P_{\rm d}/\beta^3\). The thick dashed line represents the estimate for the uncovered disk. The thick solid line shows the same for the disk with undoped cap. The thin solid line represents the qualitative estimate \(\beta=s^{1/3}\) without coefficients. Circles corresponds to the experimental data for the power achieved and corresponding estimates for the background loss \(\beta\). All future experiments and numerical simulations and estimates are expected to give values of \((\beta, s)\), that are below the red dashed line in Fig.5 for the uncovered disks, and below the blue curve for the disks with anti-ASE cap. This can be interpreted as a scaling law for disk lasers .[11]
In the vicinity of the curves mentioned, the efficiency of the disk laser is low; most of the pumping power goes to ASE, and is absorbed at the edges of the device. In these cases, the distribution of the pump energy available among several disks may significantly improve the performance of the lasers. Indeed, some lasers reported using several elements combined in the same cavity.
Pulsed operation
Similar scaling laws take place for pulsed operation. In quasi continuous wave regime, the maximal mean power can be estimated by scaling the saturation intensity with the fill factor of the pump, and the product of the duration of pump to the repetition rate. At short duration pulses, more detailed analysis is required .[12] At moderate values ot the repetition rate (say, higher than 1 Hz), the maximal energy of the output pulses is roughly inversely proportional to the cube of the background loss \(\beta\); the undoped cap may provide an additional order of magnitude of mean output power, under the condition that this cap does not contribute to the background loss. At low repetition rate (an in the regime of single pulses) and sufficient pump power, there is no general limit of energy, but the required size of the device grows quickly with increase of the required pulse energy , setting the practical limit of energy; it is estimated that from a few joules to a few thousand joules can be extracted in an optical pulse from a single active element, dependently on the level of the background internal loss of the signal in the disk. .[13]
See also
References
- ↑ http://www.rp-photonics.com/thin_disk_lasers.html Thin disk lasers. Encyclopedia of Laser Physics and Technology.
- ↑ http://spiedl.aip.org/getabs/servlet/GetabsServlet?prog=normal&id=PSISDG001837000001000336000001&idtype=cvips&gifs=yes K. Ueda, N. Uehara. Laser-diode-pumped solid state lasers for gravitational wave antenna Proceedings of SPIE 1837 p.336–345 (1993)
- ↑ http://ao.osa.org/abstract.cfm?id=24598 A.Abate, L.Lund, D.Brown, S.Jacobs, S.Refermat, J.Kelly, M.Gavin, J.Waldbillig, and O.Lewis. Active mirror: a large-aperture medium-repetition rate Nd:glass amplifier Applied Optics 1837 p.351–361 (1981)
- ↑ http://www.springerlink.com/content/n7350870q8q57324/?p=c874af0585094717b13bb41e3fc548da&pi=0 A. Giesen, H. Hügel, A. Voss, K. Wittig, U. Brauch and H. Opower. Scalable concept for diode-pumped high-power solid-state lasers Applied Physics B 58 p.365–372 (1994)
- ↑ C.Stewen, K.Contag, M.Larionov, A.Giesen, H.Hugel. A 1-kW CW thin disc laser IEEE J. of Selected Topics in QE 6 p.650–657 (2000)
- ↑ Jump up to: 6.0 6.1 http://josab.osa.org/abstract.cfm?id=90157
D. Kouznetsov,
J.F. Bisson, J. Dong, and K. Ueda.
Surface loss limit of the power scaling of a thin-disk laser
JOSAB
23
p.1074–1082
(2006); [1] Cite error: Invalid
<ref>tag; name "kouz06" defined multiple times with different content - ↑ Jump up to: 7.0 7.1 http://josab.osa.org/abstract.cfm?id=84730
D.Kouznetsov,
J.F.Bisson, K.Takaichi, K.Ueda.
Single-mode solid-state laser with short wide unstable cavity
JOSAB
22
p.1605–1619
(2005) Cite error: Invalid
<ref>tag; name "uns" defined multiple times with different content - ↑ Jump up to: 8.0 8.1 8.2 http://www.opticsinfobase.org/abstract.cfm?URI=josab-25-3-338 D.Kouznetsov, J.F.Bisson. Role of undoped cap in the scaling of thin-disk lasers JOSAB 25 p.338–345 (2008)
- ↑ http://www.patentstorm.us/patents/6347109.html Stephen A. Payne, William F. Krupke, Raymond J. Beach, Steven B. Sutton, Eric C. Honea, Camille Bibeau, Howard Powel. High average power scaleable thin-disk laser US patent 6347109 p.0 (2002)
- ↑ http://patft.uspto.gov/netacgi/nph-Parser?Sect1=PTO2&Sect2=HITOFF&p=1&u=%2Fnetahtml%2FPTO%2Fsearch-bool.html&r=13&f=G&l=50&co1=AND&d=PTXT&s1=6347109&OS=6347109&RS=6347109 Beach; Raymond J. (Livermore, CA),, Honea; Eric C. (Sunol, CA), Bibeau; Camille (Dublin, CA), Payne; Stephen A. (Castro Valley, CA), Powell; Howard (Livermore, CA), Krupke; William F. (Pleasanton, CA), Sutton; Steven B. (Manteca, CA). High average power scaleable thin-disk laser USA patent 6347109 p.0 (2002)
- ↑ http://www.ils.uec.ac.jp/~dima/PAPERS/2009optmat.pdf D.Kouznetsov, J.-F.Bisson, K.Ueda. Scaling laws of disk lasers Optical Materials 31 p.754–759 (2009)
- ↑ http://www.hindawi.com/journals/rlp/aip.717414.html D.Kouznetsov., . Storage of energy in disk-shaped laser materials Research Letters in Physics 2008 p.717414 (2008)
- ↑ http://www.opticsinfobase.org/abstract.cfm?URI=josab-26-1-26 J.Speiser, . Scaling of thin-disk lasers--influence of amplified spontaneous emission JOSAB 26 p.26–35 (2009)
The content of this article previously appeared at wikipedia,
http://en.wikipedia.org/wiki/Disk_laser