CosFT
CosFT, or Cosinus Transform, refers to the integral transform with kernel \(K(x,y)=\sqrt{\frac{2}{\pi}} \cos(xy)\);
for function \(f\), the CosFT\(f\) appears as \(g\) defined with
\(\displaystyle g(x)=\,\)CosFT\(f\,(x) \displaystyle =\sqrt{\frac{2}{\pi}} \int_0^\infty \cos(xy) \, f(y) \, \mathrm d y\)
SinFT and CosFT
CosFT often appears together with SinFT;
the sine transform SinFT of function \(f\) appears as \(g=\,\)SinFT\(f\) with rofmula
\(\displaystyle g(x)=\sqrt{\frac{2}{\pi}} \int_0^\infty \sin(xy) \, f(y) \, \mathrm d y\)
It is assumed that function \(f\) decays (or, at least, quickly oscillates) at infinity, in such a way that the integral converges.
Then, SinFT\(^2=\,\)CosFT\(^2=\hat 1\), id est, the identity transform.
Numerical implementation
CosFT can be implemented numerically through the CFT transform at the uniform grid at \(N\!+\!1\) nodes; for array \(f\), the SFT \(g\) is defined with
\(g_m=\,\)CFT\(\displaystyle f_m=\) \(\displaystyle \frac{1}{2}\, f_0+\frac{(-1)^m}{2}\, f_{N} + \sum_{n=1}^{N-1} \cos\left( \frac{\pi}{N} \,m\,n \right) \, f_n\)
The Numerical recipes in C (http://numerical.recipes) suggest the implementation through routines four1 and realft; however, for the serious applications, specification "float" should be replaced to something appropriate, for example, double, or complex double. [1][2][3][4]
At given number \(N\) of nodes, the set of the nodes can be denoted with \(x_n\) for \(n=0 .. N\),
\(\displaystyle x_n=\sqrt{\frac{\pi}{N}}~ n\)
then, for \(f_n=f(x_n)\), at large \(N\gg 1\), the transform \(~g(x)=\frac{2}{\pi}\int_0^\infty f(y)\,\cos(x\,y)\,\mathrm d y~\) is approximated with
\(\displaystyle g(x_m) \approx g_m = \sqrt{\frac{2}{N}}\, \left( \frac{f_0+(-1)^m f_N}{2} + \sum_{n=1}^{N-1} \, \cos\left( \frac{\pi}{N} \,m\,n \right) \, f_n\right)\)
Eigenfunctions
Eigenfunctions \(F\) of the CosFT appear as even Oscillator functions.
The simplest of them is just Gaussian;
\(F(x)=\exp(-x^2/2)\)
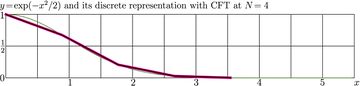
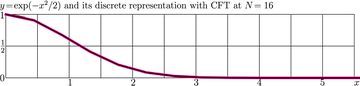
This property is used in the C++ test. The thick segmented line in the explicit plots at right show the discrete representation of the Gaussian at the discrete grid with \(N\!=\!4\) and \(N\!=\!16\).
The thin segmented line shows its SinFT transform, as it is approximated at this grid. The discrete representation and its CFT practically coincide; the deviation is smaller than the thicknesses of the lines.
References
Keywords
CosFT, FFT, Integral transform, SinFT,,,