Coshc
Coshc or coshc is elementary function, defined with
- \(\displaystyle \mathrm{coshc}(z)=\frac{\cosh(z)}{z}\)
where cosh is hyperbolic cosine,
- \(\displaystyle \cosh(z)=\cos(\mathrm i z) = \frac{\mathrm e^z+\mathrm e^{-z} }{2}\)
The derivative of coshc, id est, cosec', can be expressed with
- \(\!\!\!\!\!\!\!\!\!\!\!\!\!\!\! \cosh'(z)\) = \(\frac{\sinh(z)}{z}-\frac{\cosh(z)}{z^2} \) = \( \mathrm{sinhc}(z) - \frac{\mathrm{coshc}(z)}{z}\)
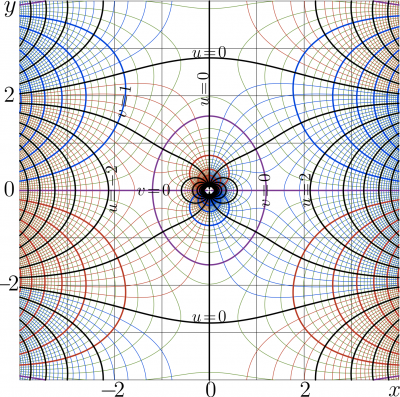
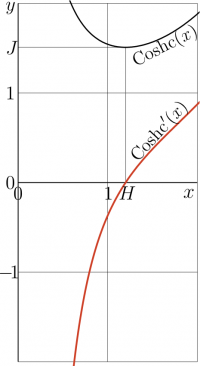
Functions \(~y\!=\!\mathrm{coshc}(x)~\) and \(~y\!=\!\mathrm{coshc}'(x)~\) are shown in the \(x\),\(y\) plane.
Coshc is related with the cosc function with the simple relations
- \(\displaystyle \mathrm{coshc}(z) = \mathrm i ~ \mathrm{cosc} ( \mathrm i z ) \) \(= \mathrm i \frac{\cos(\mathrm i z)}{\mathrm i z}\)
- \(\displaystyle \mathrm{cosc}(z) = \mathrm i ~ \mathrm{coshc} ( \mathrm i z ) \) \(= \mathrm i \frac{\cosh(\mathrm i z)}{\mathrm i z}\)
quite analogous to the relation between cos and cosh.
Minimum of \(\mathrm{coshc}(x)\) is realized at
- \( x = H\approx 1.199678640257734 ~\) ; \(~\mathrm{coshc}'(H)=0\).
- \( J = \mathrm{coshc}(H) \approx 1.50887956153832~\) .
These values are marked in the figure.
Cosch is odd function,
- \(\mathrm{coshc}(z)=-\mathrm{coshc}(-z)\)
Coshc is holomorphic function with the only singularity, namely, pole at zero. As the real argument increases from zero to infinity, the cosch decreases until its mimumim \(J\) at \(H\), and again increase, almost exponentially, to infinity.
Asymptotic expansions
At small values of the argument, coshc can be expanded as follows:
- \(\displaystyle \mathrm{coshc}(z)=\frac{1}{z}+ \frac{1}{2!} z + \frac{1}{4!}z^3 + \frac{1}{6!}z^5+ ..\)
the series converges in the whole compelex plane except zero. This series can be inverted giving the expansion for the inverse function ArcCoshc:
- \( \displaystyle \mathrm{ArcCoshc}(z)=\frac{1}{z}+ \frac{1}{2} \frac{1}{z^3}+ \frac{13}{24} \frac{1}{z^5}+ \frac{541}{720} \frac{1}{z^7}+..\)
With Mathematica software one can calculate many coefficients of this expansion. The series seems to converge while \(~\left|\frac{1}{z}\right|\!<\!\frac{1}{J}~\), id est, \(|z|>J\).
In vicinity of \(H\), coshc can be expanded as follows:
- \( \displaystyle \mathrm{coshc}(H+t)=J+\frac{\mathrm{coshc}''(H)}{2!} t^2 + \frac{\mathrm{coshc}'''(H)}{3!} t^3+..\)
which can be simplified to
- \( \displaystyle \mathrm{coshc}(H+t)=J+\frac{J}{2} {t^2} - \frac{J}{3H}{t^3}+ \frac{(8\!+\!H^2)J}{24 H^3}{t^4} -\frac{(10\!+\!H^2)J}{30 H^3}{t^5}+..\)
The replacement of \(J\) and \(H\) to their approximations gives
\( \displaystyle \mathrm{coshc}(H\!+\!t)\approx\) \(
1.50887956153832 \) \(
+ 0.75443978076916 \,t^2 \) \(
- 0.4192454853893647 \,t^3 \) \(
+ 0.4123348061601586 \,t^4 \) \(
- 0.3332232452918583 \,t^5 \) \(
+ 0.2798560879822419 \,t^6 +..\)
With Mathematica software one can easy calculate a dozen coefficients of this expansion and evaluate them.
The InverseSeries service allows to express the expansion of the inverse function ArcCoshc:
- \( \displaystyle \mathrm{ArcCoshc}(J+t)=H+\left(\frac{2 t}{J}\right)^{1/2} + \frac{1}{2H} \left(\frac{2 t}{J}\right) -\frac{4+3H^2}{72\,H^2} \left(\frac{2 t}{J}\right)^{3/2} + O(t^2)\)
The replacement of \(J\) and \(H\) to thier approximations gives the approximation
\(
\mathrm{ArcCoshc}(J+t)=
1.199678640257734 \) \(
+1.1512978931181814\, t^{1/2} \) \(
+0.3682894163539221\, t\) \(
+0.12249075985507865\, t^{3/2} \) \(
-0.11091147932942629\, t^2 \) \(
+0.02623011940391186\, t^{5/2}\) \(
+O(t^3)\)