Iterated Cauchi

Iterated Cauchi is algorithm of iterative solution of the Transfer equation

\( \!\!\!\!\!\!\!\! (1) ~ ~ ~ T(F(z))=F(z+1) \)

where \(~T~\) is given transfer function and \(~F~\) is holomorphic solution with certain properties.

It is assumed that the transfer function \(T\) is holomorphic and its inverse function \(U=T^{-1}\) is also holomorphic in the working range of valies.

It is assumed that there exist fixed points \(Z_{\mathrm o}\) and \(Z_{\mathrm c}\) such that

\(T(Z_{\mathrm o})=Z_{\mathrm o}~\), \(~ U(Z_{\mathrm o})=Z_{\mathrm o}\)

\(T(Z_{\mathrm c})=Z_{\mathrm c}~\) , \(~ U(Z_{\mathrm c})=Z_{\mathrm c}\)

It is assumed that \(F(z)\) is holomorphic at least in the strip \(\Re(z)\le 1\), and

\( \displaystyle \lim_{y\rightarrow +\infty} F(x+\mathrm i y)= Z_{\mathrm o}~\), \(~\displaystyle \lim_{y\rightarrow +\infty} F(x- \mathrm i y)= Z_{\mathrm c}\)

The Cauchi integral

Holomorphic function \(F\) satisfies the Cauchi integral formula

\(\!\!\!\!\! (9) ~ ~ ~ \displaystyle F(z)=\frac{1}{2\pi \mathrm i} \oint_{\Omega~} \frac{f(t)}{t\!-\!z} \mathrm d t\)

the contour of integraiton goes around point \(x\) in the positive direction (counter-clock vice).

The specific choice of the contour allows to express values f(t) through the left hans side of (9) with the Transfer equation. Let the contour Ω consist of 4 parts:
A. integration along the line \(\Re(t)=1\) from \(t = 1−\mathrm i A\) to \(t = 1+\mathrm i A\),
B. integration from point \(t = 1+\mathrm iA\) to \(t = −1+ \mathrm i A\), passing above point \(z\),
C. integration along the line \(\Re(t) = −1\) from \(t = −1+ \mathrm i A\) to \(t = −1−\mathrm iA\),
D. integration from point \(t = −1−\mathrm i A\) to \(t = 1−\mathrm i A\), passing below point \(z\).

This leads to the following equation:

\(\!\!\!\!\! (10) ~ ~ ~ \displaystyle F(z)= \frac{1}{2\pi} \int_{-A}^{A} \frac{F( 1+ {\rm i} p)~ {\rm d} p}{1+{\rm i} p - z } - \frac{1}{2\pi} \int_{-A}^{A} \frac{F(-1+{\rm i} p)~ {\rm d} p}{-1+{\rm i} p - z } \displaystyle - \frac{f_{\mathrm{up}}}{2\pi \mathrm{i}} \int_{-A}^{A} \frac{\mathrm{d} t}{t-z} + \frac{f_{\mathrm{down}}}{2\pi \mathrm{i}} \int_{-A}^{A} \frac{\mathrm{d} t}{t-z} \)

where \(f_{\mathrm{up}}\) and \(f_{\mathrm{down}}\) are some mean values in vicinity of the upper and the lower parts of the contour (parts B and D). At large \(A\gg 1\), these values can be approximated with \(Z_{\rm o}\) and \(Z_{\rm c}\); then, the transfer equationgives the integral equation for the approximaiton \(F_A\) of the solution \(F\):

\(\!\!\!\!\! (11) ~ ~ ~ \displaystyle F_A(z)= \frac{1}{2\pi} \int_{-A}^{A} \frac{T(F_A({\rm i} p))~ {\rm d} p}{1+{\rm i} p - z } - \frac{1}{2\pi} \int_{-A}^{A} \frac{U(F_A({\rm i} p))~ {\rm d} p}{-1+{\rm i} p - z } \displaystyle + \mathcal{K}(z) \)

where

\(\!\!\!\!\! (12) ~ ~ ~ \displaystyle \mathcal{K}(z)= Z_{\rm o} \left(\frac 12 - \frac{1}{2 \pi \mathrm i} \ln \frac {1-\mathrm i A+z} {1+\mathrm i A-z} \right) + Z_{\rm c} \left(\frac 12 - \frac{1}{2 \pi \mathrm i} \ln \frac {1-\mathrm i A-z} {1+\mathrm i A+z} \right) \)

The solution \(F(z)\) along the imaginary axis is approximated with

\(F(iy) \approx f(x)\)

where \(f\) is solution of the "nonlinear Friedhoml of second kind",

\(\!\!\!\!\! (13) ~ ~ ~ \displaystyle f(y)= \frac{1}{2\pi} \int_{-A}^{A} \frac{T(f(p))~ {\rm d} p}{1+{\rm i} p - {\rm i}y } - \frac{1}{2\pi} \int_{-A}^{A} \frac{U(f(p))~ {\rm d} p}{-1+{\rm i} p - {\rm i}y } \displaystyle + \mathcal{K}({\rm i } y) \)

At the representation of some nesh, the equation (13) can be interpreted as assignment of the iteration procedure to approximate the solution of the Transfer equation.

The convergence of the iteration (13) depends on the order of update of values of \(f\). At the parallel updating, the procedure usually diverges; but it converges well at some mixed order of updates. In particular, with the update of the odd nodes from left to right and then the update of even nodes from right to left, of order of a ten significant digits of the solution can be achieved within few tens of iterations.

From the solution \(f\), the approximation for \(F\) is defined with equation (11).

Application of the Iterated Cauchi

The Iterated Cauchi is used to evaluate the tetration to base \(b=\mathrm e\approx 2.71~\) .

First iterations for the Tetration to Sheldon base; \(f=f(x)\) versus \(x\)

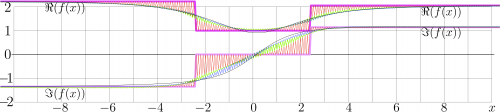
The same algorithm, with minimal modification, allows the evaluation of tetration to the complex base, and, in particular, to the tetration to Sheldon base

\(b=s\approx 1.52598338517+0.0178411853321 i\).

This base is used in this section as an examle. The 0th iteration for \(f\) are shown in the figure; the 0th approximation is shown with thick light lines. The 9th iteration is shown with thin black lines; visually, this approximation is already not distinguishable from the precise solution. For this evaluation, \(A=32\) and number of nodes \(N=2048\).

The distribution of the resulting evaluation of tetration \(\mathrm {tet}_s(z)\) along the lines \(z=0.5+\mathrm i y\) and \(z=-0.5+\mathrm i y\) will be shown in the next figure. (As soon as I arrange the labels, leyend and load it.) The thick lines show the initial approximation for \(\mathrm{tet}_s(z)\). The thin black lines show the test: \(\exp(a\cdot \mathrm{tet}_s(-0.5+\mathrm i y))\) and \(\ln(\mathrm{tet}_s(+0.5+\mathrm i y))/a\). Visually, the these lines perfectly match the thick lines.

Keywords

Tetration, Cauchi formula, Superfunction