Kneser function
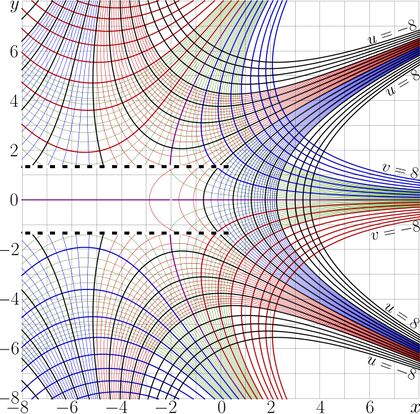Complex map of the Kneser function : \(u\!+\!\mathrm i v=\mathrm{Kneser}(x\!+\!\mathrm i y) \)
Kneser function is iterate half go the natural exponential.
The Keneser function "Kneser" is solution \( \varphi \) of equation
\( \varphi(\varphi(z)) = \exp(z) \)
This article desctibes this function.
View
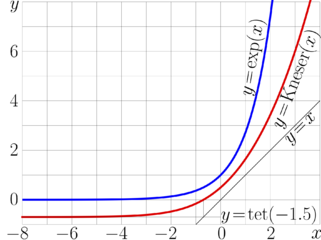
View of the Kneser function is shown at right.
Complex map of this function is shown at the top.
The explicit plot is shown below. For comparison, the identity function and exponential are also plotted.
The function \( \varphi \) above is denoted "Kneser" after German researcher Hellmuth Kneser (1898.04.16, Tartu (Dortpart), Estonia - 1973.08.23, Tubingen), shown in the right bottom side of the figure.
History
First, the equation above appears in 1950 article [1] by Hellmuth Kneser, entitled
Reelle analytische Lösungen der Gleichung \(\varphi(\varphi(x))=\mathrm e^x\)
The existence to the solution \( \varphi \) had been indicated, although no algorithm for the evaluation had been suggested.
The representation of the solution had been suggested through the natural tetration tet and the arctetration ate:
\( \varphi(z)= \mathrm{tet}\left( \frac{1}{2} + \mathrm{ate}(z) \right) \)
where tet is natural tetration, id est, solution \( F \) of the transfer equation
\( F(z+1)=\exp(F(z))\)
and ate is the arctetration, the increase function, \( \mathrm{ate}=\mathrm{tet}^{-1} \)
However, no conditions for the uniqueness of tetration and arctetration had been specified.
Ni this sense, neither uniqueness, nor efficient way of the evaluation har been supplied that time.
Definition
The simplest and, perhaps, the most explicit
In general, the solution of the equation above is not unique. The special additional condition is necessary for the uniqueness.
Iterate
References
- ↑ http://www.digizeitschriften.de/dms/img/?PPN=GDZPPN002175851 H.Kneser. Reelle analytische Lösungen der Gleichung \(\varphi(\varphi(x))=e^x\). Equationes Mathematicae, Journal fur die reine und angewandte Mathematik {\bf 187} 56–67 (1950)
