Linear approximation
Linear approximation refers to the simple model of any phenomenon, based on the linear function.
For the case of single variable, say, \(t\), the linear approximation is defined with linear function,
\(F(t)=A+Bt\)
where \(A\) and \(B\) are parameters, that do not depend on \(t\).
Tangent approximation
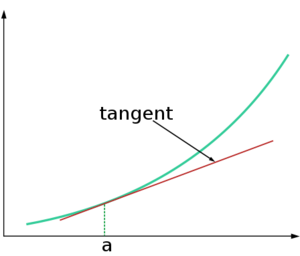
If value of function \(f\) at some point, say, at zero, is known, id est, \(f_0=F(o)\) and, also, the derivative at this point is known, id est, \(f_1=f'(0)\), the tangent approximation is the linear approximation with parameters \(A=f_0\) and \(b=f_1\).
Example of the tangent approximation is shown in figure at top.
Extrapolation
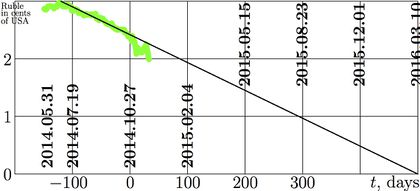
In application of mathematical analysis, all functions are known with some finite precision, and the first approximation may neglect fluctuation of some quantity. In many case, the linear approximation can be used as a simple model.
The figure at right shows the price of ruble in the american cents (penny, 1/100 of the USA dollar). Since the application of serious sanctions on Russia, duding more than 3 month, the price of ruble can be approximated with linear function, shown with straight black line. Abscissa zero corresponds to the data of construction of the linear approximation. The thick green line corresponds to the experimental data up to 2014.10.27 by [2]. The black straight line represents the linear approximation.
Usually, any approximation allow extrapolation, prediction of properties of function outside the range, used for the construction. In the example in figure at right, the interpolation predicts the crash of the Russian financial (and, perhaps, also political) system within 500 days since the data of construction of the approximation. This quantity is determined by the intersection of the straight lie with the abscissa axis.
However, before the intersection, the approximation may become invalid; as any other scientific concept, the linear approximation has limited range of validity. On the base of the linear approximation, shown in the figure, one may expect, that in 2015, the price of ruble becomes less than one penny, and some kind of the decay of Russia in 2016 (or even before). On the other hand, the general observations indicate that the prediction of revolutions in not possible; so, even if Russia indeed collapses in 2015 or 2016, this should not be considered as general justification of use of the linear approximation for extrapolation of economical and historical events. Therefore, one may expect the linear approximation to become invalid before the serious territorial and/or administrative rearrangement of Russia.
The example above is methodically correct, because, at the time of the loading, the evolution of the quantity (price of rouble) is not yet known. In other words, it is not known, how far the approximation describes the evolution of the quantity. In this sense, it is typical case of application of any extrapolation.
Measurement
The physical concept of measurement is based on the linear approximation of some dependences. One quantity is supposed to be proportional to some number of application of some action, to the number of iterate of some procedure. For example, if the procedure is step along the road, then, counting of the steps can be considered as a way to measure the length of the road. Any physical quantity should imply the way of the measurement.
For example, the linear approximation cannot be applied to measure the degree of holiness of some holly object; for this reason, holiness should be qualified as religious, but not physical (and not scientific) concept.
References
- ↑ http://en.wikipedia.org/wiki/Linear_approximation
- ↑ Jump up to: 2.0 2.1 https://www.mataf.net/en/currency/converter-USD-RUB The maximum was reached on 27 Oct 2014 1 000.00 US Dollar = 41 984.50 Russian Ruble The minimum on 22 Feb 2009 1 000.00 US Dollar = 27.60 Russian Rubble