NemBran
NemBran is holomorphic function that expresses the branch point of the Nemtsov function \(\mathrm{Nem}_q\) versus parameter \(q\). While, only analysis for the real \(q\) is presented. For real \(q\) function \(\mathrm{Nem}_q\) is real–holomorphic, id est, \(\mathrm{Nem}_q(z^*)=\mathrm{Nem}_q(z)^*\); this simplifies the consideration.
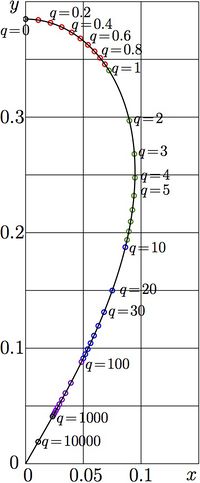
For real values of the argument, the Parametric plot of function NemBran is shown in figure at right:
\(x=\Re(\mathrm{Nembran}(q))\)
\(y=\Im(\mathrm{Nembran}(q))\)
Description
The Nemtsov function is defined with
\(\mathrm{Nem}_q(z)=z+z^3+q z^4\)
This function is suggested as an example of non–symmetric transfer function that allows the exotic iterate.
Derivative of the Nemtsov function can be written as follows:
\(\mathrm{Nem}_q^{\prime}(z)=1+3\,z^2+4\, q\, z^3\)
Let \(z_0=\mathrm{NemBra}(q)\) such that \(\Re(z_0)>0\) be solution of equation
\(\mathrm{Nem}_q^{\prime}(z)=0\)
The inverse function \(\mathrm{ArqNem}_q=\mathrm{ArqNem}_q^{-1}\) has 3 branch points, and one of them is expressed as
\(\mathrm{Nembran}(q)=\mathrm{Nem}_q(\mathrm{NemBra}(q))\)
This representation is used for evaluation of function \(\mathrm{NemBran}\). However, function NemBra should be implemented. It can be expressed as follows:
Let \(~ \rho=-1-8q^2+4\sqrt{q^2+4q^4}\)
Let \(~ V=\rho^{1/3}\)
Then \(~ \displaystyle \mathrm{NemBra}(q)=\frac{1}{4q}\left(-1+V+1/V\right)\)
Application
Function NemBran is necessary to determine the cut lines of function ArqNem, which, in its turn, necessary for evalution of function AuNem, which is Abel function for the Nemtsov Function.
Functions SuNem and AuNem are used to express the non-integer iterates of the Nemtsov function. The Nemtsov function is used as an example to check the exotic iterate for the update of the book Superfunctions.
It is common, that the careful implementation of the inverse function is necessary for the implementation of the Abel function or superfunction for any non–trivial transfer function; then non–integer iterates of the transfer function can be expressed and evaluated.
On the most of applications, the only real–values functions are used. However, for the detection of possible mistakes, the new fundamental functions should be implemented in the most of the complex plane, id est, for the complex argument.
Refrerences
Keywords
Abel function, ArcNem, ArkNem, ArqNem, AuNem, Branch point, Inverse function, Nemtsov function, SuNem, Superfunction,