Decay heat

Decay heat (Остаточное тепловыделение) it thermal energy that is released at the decay, relaxation of unstable isotopes; usually the term applies to the relaxation processes in the nuclear waste or in the nuclear reactors after the shutting down.

Fit estimating the relaxation heat

Some sites suggest the online software to estimate the relaxation heat . No comparison of the results of such a simulation to the experimental data is available.

The approximation of the relaxation power \(P\) with elementary function

\(\!\!\!\!\!\!\!\!\!\!\! (1) ~ ~ ~ \displaystyle P = P_0 Q \left( \left(\frac{t_0}{\tau-\tau_{\rm s}}\right)^{\!1/5} - \left(\frac{t_0}{\tau_{\rm s}}\right)^{\!1/5} \right)\)

is widely announced . Such an estimate assumes that the reactor worked with power \(P_0\) during time \(\tau_{\rm s}\); then the estimate returns the heat power released at time \(\tau\) since the beginning of the chain reaction; \(Q=0.066\) and \(t_0\) are the fitting parameters. (For such a formula, it would be possible to use a single fitting parameters; perhaps, the designer wanted to keep the first parameter dimensionless.)

The uncertainty of parameter \(t_0\) seem to be large; wikipedia implicitly suggests value \(t_0=1\)second, without to cite any publication that would justify the choose of this value; no comparison with experimental data is available in the free access pages.

Various authors reproduce estimates similar to (1) without to understand its meaning. For example, ref. suggests an estimate similar to (1), but without the dimensional factor \(t_0\); in such a way they suggest the formula that is just wrong. If the nuclear engineers cannot perform even the elementary dimensional analysis, then one should not wonder why the nuclear reactors sometimes melt down and explode soon after the shut-down.

According to Wikipedia, many authors believe that such formula with \(t_0\!=\!1\)second gives the correct order of magnitude of the power generated in the reactor after the shutdown. This assumption is used below for the example with the Chernobyl disaster

Estimates for the Chernobyl reactor

For the Chernobyl reactor, \(P_0\approx 3\)GW; the time of operation \(t_s \approx 3\)years . Assume that within a day since the explosion, the suicide workers had picked up the active rods and collected them into a heap inside the wreckage of the building, disabling the convectional cooling. Then, the energy released within the next day can be estimated as follows:

\(\displaystyle E=\int_{t_s+1\rm day}^{t_s+2\rm days} P(t) {\rm d}t \) ;

this gives

\(\displaystyle E\approx 0.066 \cdot 3{\rm GW} \int_{t_{\rm s}+1\rm day}^{t_{\rm s}+ 2 \rm days } \left( \left(\frac{t_0}{t_s+t}\right)^{\!\!1/5}-\left(\frac{t_0}{t_s}\right)^{\!\!1/5} \right) {\rm d} t \) .

Assuming that \(t_0=1\)second, this gives the estimate

\(\displaystyle E=0.2 {\rm GW} \cdot 58162 {\rm second} \approx 10 \rm TJ = 10^{13} J\)

The vaporization heat of Uranium is 417 kJ/mol , id est, \(10^6\)J/kg; this gives the estimate that the relaxation heat would be sufficient to evaporate into the atmosphere \(\rm 10^{12} J/ (10^6 J/kg) =10^6kg \) of the nuclear fuel; this is of order of magnitude of the mass of the reactor. The attempts to "extinguish" the burning reactor with the sacrifice of the firefighters-kamikaze could slow down the process of the vaporization extending it to few days.

The Russian nuclear analyst Viktor Kirienko had predicted the similar scenario for the Fukushima disaster; however, in the case of Fukushima, there was no primary explosion due to the chain reaction; and the conventional cooling system failed only after a day since the shut-down; then, the availability of the sea–water for the external cooling allowed to avoid the worst case.

In the popular description of the Chernobyl disaster, the heat that caused vaporization of the nuclear fuel is attributed to the burning of the graphite (used as moderator). The estimate above shows that even after the shut-down, the energy of the decay heat greatly exceeds that due to the graphite burning: the burning of carbon provides the temperature of only few thousands degree, that would be barely sufficient to melt the comparable amount of uranium.

Thе bomb used in Hiroshima in 1945 released of order of \(\rm 60 TJ=6\cdot 10^{13} J\); however, the contamination due to the Cherbobyl lasted during many years (and is expected to last during a century), making the effect of Chernobyl for orders of magnitude worce than that due to the Hiroshima bombing.

Estimates for the Fukushima reactors

Estimates for Fukushima by

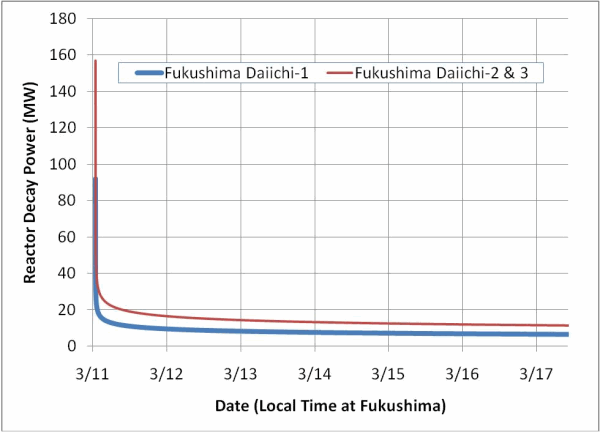
The estimates show, that after the Fukushima disaster (2011 March, Japan) the decay heat also remains pretty high (Several MegaWatt), and only the continuous forced cooling prevents the evaporation of the nuclear fuel to the atmosphere.

Extinguishing of the reactor

At a failure of the cooling system, the reactor burns, even if the chain reaction is shut down; it cannot be "extinguished". The only one can do with it is to cool it during a time comparable to the time of the operation. (Then, the generation of the decay hit reduces, and the fuel can be recycled). The dispersion of the fuel on a wide area (that would allow its convective cooling) is better, than the collection into a heap, which allows the evaporation into the atmosphere: in the first case, the dispersion on an area of few square kilometers would be sufficient, an, when the short–living isotopes decay, the contaminated layer can be buried. In the second case, the contaminated area counts thousands of square kilometers, and the handling is more difficult. In this sense, the collection of the active rods, performed by the suicide workers at Chernobyl, made the tragedy worse instead of mitigate it. The decision to collect the active rods into the wreckage of the reactor can be attributed either to the bad will of the ruling soviet veterans, or to their poor education: perhaps, they did not know about the decay heat.

Conclusions

The decay heat plays the dominant role in the spreading of the radioactive contamination at the nuclear reactor accidents. The estimates show that, by default, the nuclear reactor melts and vaporizes the most of the nuclear fuel into the atmosphere, even if the chain reaction is stopped; only the permanent work of cooling pumps and the good will of the operators prevent this.

According to publications, the decay heat of the nuclear fuel after the reactor shutdown is never used to get the energy, nor even to power the pumps that deliver the coolant to the reactor. After to stop the chain reaction, the reactors happen to be completely dependent on the external sources of energy (electric power supply lines, or the emergency diesel generators). At the failure, the decay heat tends to convert the reactors to the nuclear chimneys, and the self-sacrifysing efforts of the suicide fire-fighters are required to cool it, keeping the most of the nuclear fuel inside the reactor.

The important question of the nuclear energetics, that remains unanswered since the Fukushima disaster is:
Why the decay heat cannot be used to power the emergency cooling systems?

Keywords

Chernobyl disaster, Fukushima disaster, Physics, Nuclear accidents, Nuclear disasters