Serega function

Serega function is nongolomorphic function \(\mathrm{Serega}\) of complex variable \(z\) such that

\(F(z)=x+\mathrm i ~ \exp(\mathrm i ~ z^*)\)

where the asterisk means the complex conjugation.

The Serega function is not holomorphic, and, therefore, not differentiable, id est, the derivative depends on the direction of variation of the argument. However, the derivatives with respect to real and imaginary parts of the argument exist.

Appearance

In the Fluid mechanics, the Serega function describes transfer from the Euler coordinates to the Lagrangian coordinates for the movement of the surface waves of an idealized liquid. The real and imaginary parts of the argument have sense of the labels of the particles of the liquid while the real and imaginary parts of the value have sense of the Cartesian coordinates of the liquid.

The coordinates of the particles of the liquid can be written in such a way:

\( X=X(x,y,t)= \Re( \mathrm{Serega}( k x - \omega t + \mathrm i y))\)

\( Y=Y(x,y,t)= \Im( \mathrm{Serega}( k x - \omega t + \mathrm i y))\)

where \(x\) and \(y\) determine the particle, while \(X\) and \(Y\) are Cartesian coordinates of the particle at time \(t\).

Parameter \(k\) has sense of wavenymber.

Parameter \(\omega\) has sense of frequency.

Particles with \(y=y_s=\mathrm {constant}\) can be interpreted as surface of the liquid, at least while \(y<0\).

The components of velocity

\(u=\dot X=u(x,y,t)\)

\(v=\dot Y=v(x,y,t)\)

are derivatives of functions \(X\) and \(Y\) with respect to the last argument.

WIth the inverse function \(\mathrm{ArcSerega}\), velocities can be expressed in terms of the Cartesian coordinates:

\(U=U(x(X,Y,t), y(X,Y,t), t)=u(x,y,t)\)

\(V=V(x(X,Y,t), y(X,Y,t), t)=v(x,y,t)\)

where

\(x(X,Y,t)= \frac{1}{k}\left( -\omega t + \Re(\mathrm{ArcSerega} ( kX - \omega t +\mathrm i k Y )) \right)\)

\(y(X,Y,t)= \frac{1}{k} \Im(\mathrm{ArcSerega} ( kX - \omega t +\mathrm i k Y ))\)

These velocities satisfy the Navier-Stokes equation for the Eulerian liquid (without viscosity). The surface tension of the liquid is neglected. The liquid is treated as non–compressible. The gravitational force with acceleration \(g=\omega/k\) should be applied as the "external force".

ArcSerega

Map of the ArcSerega function

While Serega function is not holomorphic, the inversion is not so easy as inversion of factorial or tetration, and ArcSerega cannot be approximated inverting the power series of Serega. In the implementation of ArcSerega, it is treated as pair of functions of pair of variables.

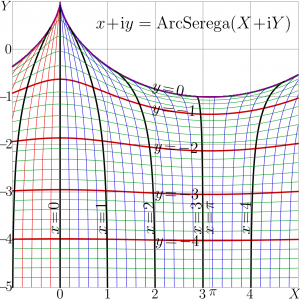
The Complex map of ArcSerega is shown in figure at right. ArcSerega is also non–holomorphic; therefore, the line of constant real part are not orthogonal to the lines of constant imaginary part.

ArcSerega is periodic with period \(2\pi\)

ArcSerega is Symmetric with respect to the real part of argument: \(\mathrm{ArcSerega}(X+\mathrm i Y) = \mathrm{ArcSerega}(-X+\mathrm i Y)\)

At large positive values of the imaginary part of the argument, ArcSerega behaves in a way, similar to logarithm. Usually such a range of values is not used in the applications, and the part of the complex map above the cycloid \(X+\mathrm i Y=a-\sin(a) + \mathrm i \cos(a)\), \(a\in \mathbb R\) is left empty at the figure.

Ethimology

The identifier of the Serega function is chosen as slightly modified first name of Sergey Kuznetsov, who thinks, that in the idealized wave, the movement is rotorless. .

The Serega function is expected to be useful in analysis of the break of waves, as the important basis function to approximate more complicated solutions of the Navier-Stokes with appropriate combinations of the Serega functions

Keywords

Navier-Stokes equation, Sergey Kuznetsov, Fluid dynamics