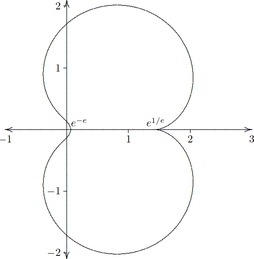
Shell-Thron region
Shell-Thron region (Область Тронной Ракушки) is subset of set of complex numbers \(b\) such that there exist limit
\( \displaystyle L = \lim_{n\rightarrow \infty} \exp_b^n(1) \)
This \( L \) is a fixed point of \(\exp_b\).
The Shell-Thron region is shown in figure at right; it is area inside the loop.
William Harold Paulsen
In 2018, William Harold Paulsen suggests the following definition [1]:
We say that the base \(b\) is in the Shell-Thron region if the sequence of values \( \{ b, b^b, b^{b^b}, b^{b^{b^b}}, ... \}\) converge to a finite fixed point.
Evaluation of tetration
For \(b \in \) Shell-Thron region, tetration \( \mathrm{tet}_b \) can be evaluated through its asymptotyc expansion at large values of the real part of its argument, using the transfer equation
\( \exp_b(\mathrm{tet}_b(z))=\mathrm{tet}_b(z\!+\!1) \)
For values \( b \) outside this region, the asymptotic expansion at complex fixed points of exponential can be used for large negative values of argument of the tetration. Then, the appropriate requirements on asymptotic behavior of tetration are postulated in order to provide its uniqueness; the tetration should approach its fixed points at large values of the imaginary part of its argument.
For \(v\) at the margin of the Shell-Thron region, none of the methods above is sufficient to evaluate \( \mathrm{tet}_b \), although the representation through the Cauchi integral still works [2], except case of real \( b \le \exp(1/\mathrm e) \approx 1.44466786101\) ; then the special expansion is required [3][4]
In particular, the representation of tetration through the Cauchi integral [2] can be used for the Sheldon base, specific value \(b=1.52598338517 + 0.0178411853321~ {\rm i}\), that is close to the margin of the Shell-Thron region, see Tetration to Sheldon base [5]. However, no any specific difficulties in use of the Cauchi integral for the evaluation is detected, as base \(b\) approaches the margin of the Shell-Thron region [6]
References
- ↑ 1.0 1.1
https://www.researchgate.net/publication/325532999_Tetration_for_complex_bases
https://link.springer.com/article/10.1007/s10444-018-9615-7 William Harold Paulsen. Tetration for complex bases. Advances in Computational Mathematics, volume 45, pages 243–267(2019) Abstract In this paper we will consider the tetration, defined by the equation \( F(z+1)= b^F(z)\) in the complex plane with \( F(0)=1\), for the case where \(b\) is complex. A previous paper determined conditions for a unique solution the case where \( b \) is real and \(b>e^{1/e}\). In this paper we extend these results to find conditions which determine a unique solution for complex bases. We also develop iteration methods for numerically approximating the function F(z), both for bases inside and outside the Shell-Thron region. .. We say that the base \(b\) is in the Shell-Thron region if the sequence of values \( \{ b, b^b, b^{b^b}, b^{b^{b^b}}, ... \}\) converge to a finite fixed point. .. - ↑ 2.0 2.1 http://www.ams.org/mcom/2009-78-267/S0025-5718-09-02188-7/home.html
https://mizugadro.mydns.jp/PAPERS/2009analuxpRepri.pdf D.Kouznetsov. Analytic solution of F(z+1)=exp(F(z)) in complex z-plane. Mathematics of Computation, v.78 (2009), 1647-1670. - ↑
http://www.ams.org/journals/mcom/2010-79-271/S0025-5718-10-02342-2/home.html
https://mizugadro.mydns.jp/PAPERS/2010sqrt2.pdf D.Kouznetsov, H.Trappmann. Portrait of the four regular super-exponentials to base sqrt(2). Mathematics of Computation, 2010, v.79, p.1727-1756. - ↑
https://link.springer.com/article/10.1007/s00010-010-0021-6
https://mizugadro.mydns.jp/PAPERS/2011uniabel.pdf H.Trappmann, D.Kouznetsov. Uniqueness of holomorphic Abel functions at a complex fixed point pair Aequationes Mathematicae, v.81, p.65-76 (2011) - ↑
http://www.ils.uec.ac.jp/~dima/BOOK/443.pdf
http://mizugadro.mydns.jp/BOOK/444.pdf D.Kouznetsov. Superfunctions. 2020 - ↑ The number \(b=1.52598338517 + 0.0178411853321~ {\rm i}\) has been suggested by Sheldon Livenstein; so, it is denoted with term Sheldon base. Sheldon Livenstein expected, it is difficult to evaluate tetration to this base. Even after demonstration of the efficient evaluation of tetration to Sheldon base, Sheldon Livenstein did not present any reason, why tetration to namely Sheldon base should be especially interestesting. Perhaps, this number is somehow used in some secret investigation, that Sheldon Livenstein cannot yet reveal.
- ↑ https://www.researchgate.net/publication/325532999_Tetration_for_complex_bases Tetration for complex bases Article (PDF Available) in Advances in Computational Mathematics · June 2018 with 201 Reads DOI: 10.1007/s10444-018-9615-7 Cite this publication William Harold Paulsen 16.23 Arkansas State University - Jonesboro// Abstract// In this paper we will consider the tetration, defined by the equation F(z+1)=bF(z) in the complex plane with F(0)=1, for the case where b is complex. A previous paper determined conditions for a unique solution the case where b is real and b > e1/e. In this paper we extend these results to find conditions which determine a unique solution for complex bases. We also develop iteration methods for numerically approximating the function F(z), both for bases inside and outside the Shell-Thron region.
Keywords
Exp, Iterate, Shell-Thron region, Superfunction, Superfunctions, Tetration, Tetration to Sheldon base,