SuZex

Fig.1. \(y\!=\!\mathrm{SuSex}(x)~\), thick blue line, and \(y\!=\!\mathrm{zex}(x)\!=\!x\mathrm e^x\), thin line

Fig.2. Map \(u\!+\!\mathrm i v=\mathrm{SuZex}(x\!+\!\mathrm i y)\)

SuZex is superfunction of ArcLambertW, denoted also as zex, \(\mathrm{zex}(z)=z \exp(z)\).

\(\!\!\!\!\!\!(1) ~ ~ ~ \mathrm{SuZex}(0)=1\)

\(\!\!\!\!\!\!(2) ~ ~ ~ \mathrm{SuZex}(z\!+\!1)=\mathrm{zex}\Big(\mathrm{SuZex}(z)\Big)\)

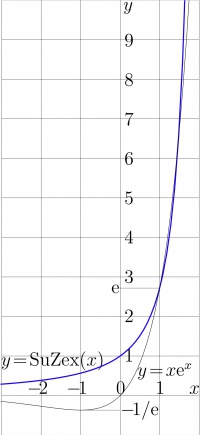
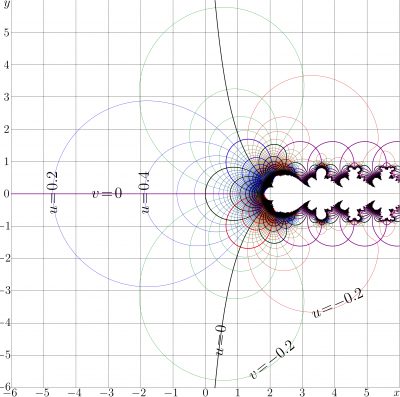
The explicit plot of function SuZex is shown in Figure 1 in comparison with that function zex. The Complex map of SuZex is shown in Figure 2. More detailed map is available in the article SuZex approximation.

Definition

The first two terms of the asymptotic expansion of SuZex can be used as the definition.

Let \(~ ~\mathrm{zex}(z)\!=\!z\exp(z)\)

Let \(~ \displaystyle f(z) =\frac{-1}{z}+\frac{\ln(z)}{2z^2}\)

Let \(~ F_n(z)=\mathrm{zex}^n\big( f(z\!-\!n) \Big)\)

Let \(~ x_n\) be real solution of equation \(F_n(x_n)=1\).

Then, SuZex is defined with

\(\!\!\!\!\!\!(3) ~ ~ ~ \displaystyle \mathrm{SuZex}(z)= \lim_{n\rightarrow \infty} \mathrm{zex}\Big( F_n(x_n\!-\!z) \Big)\)

Behavior

SuZex decays at infinity, behaving similat to \(z\mapsto 1/z\); but along the positive direction of the real axis it shows fast growth, similar to that of the SuperFactorial and that of tetration to base \(b>\exp^2(-1)=\exp(1/\mathrm e)\).

Asymptotic expansion

The asymptotic expansion of SuZex can be developed using the definition; it is described below in the Mathematica language.

Mathematica code

Somehow, Mathematica's Series function dislikes the leading sign "-" in the argument of Log, adding some innecessary \(\pi \mathrm i\); so, in the code below, there is Log[z] instead of Log[-z]. However, this does not affect the expansion; and Log[z] can be replaced to Log[-z] in the final expression. From this deduction, the only requirement is smportant, that at z\(\mapsto\) z+1, the function changes Log[\(\pm\)z] \(\mapsto\) Log[\(\pm\) z] Log[1+1/z] with following expansion at small values 1/z. In such a way, the expansion does not depend on the leading sign of the argument in the logarithm in the expresion for \(\ell\).

zex[z_] = z Exp[z];

Foo[z_] = -1/z + a Log[z]/z^2

Soo = Series[Foo[z+1]-zex[Foo[z]], {z,Infinity,3}]
Eoo = Coefficient[Soo,1/z^3]
Ao = Extract[Solve[Eoo==0, a], 1]
F2o[z_] = ReplaceAll[Foo[z], Ao]

F20[z_] = F2o[z] + (a Log[z]^2 + b Log[z] + c)/z^3

S2o = Series[F20[z+1] - zex[F20[z]], {z,Infinity,4}]
S20 = ReplaceAll[S2o, Log[1/z] -> -L]
E2o = Coefficient[S20, 1/z^4]
E22 = Coefficient[E2o, L^2]
A1 = Extract[Extract[Solve[E22==0, a], 1], 1]
E2A = ReplaceAll[E2o, A1]
E21 = Coefficient[E2A, L]
B1 = Extract[Extract[Solve[E21==0, b], 1], 1]
E2B = ReplaceAll[E2A, B1]
C1 = Extract[Extract[Solve[E2B==0, c], 1], 1]
F3o[z_] = ReplaceAll[F20[z], {A1, B1, C1}]

F30[z_] = F3o[z] + (a Log[z]^3 + b Log[z]^2 + c Log[z] + d)/z^4

S3o = Series[F30[z+1] - zex[F30[z]], {z, Infinity, 5}]
S30 = ReplaceAll[S3o, Log[1/z] -> -L]
E3o = Coefficient[S30, 1/z^5]
E33 = Coefficient[E3o, L^3]
A3 = Extract[Extract[Solve[E33==0, a], 1], 1]
E3a = ReplaceAll[E3o, A3]
E32 = Coefficient[E3a, L^2]
B3 = Extract[Extract[Solve[E32==0, b], 1], 1]
E3b = ReplaceAll[E3a, B3]
E31 = Coefficient[E3b, L]
C3 = Extract[Extract[Solve[E31==0, c], 1], 1]
E3c = ReplaceAll[E3b, C3]
D3 = Extract[Extract[Solve[E3c == 0, d], 1], 1]
F4o[z_] = ReplaceAll[F30[z], {A3, B3, C3, D3}]

F40[z_] = F4o[z] + (a Log[z]^4 + b Log[z]^3 + c Log[z]^2 + d Log[z] + e)/z^5
S4o = Series[F40[z+1] - zex[F40[z]], {z, Infinity, 6}]

(* At this step, F40 is asymptotic representation of superfunction of zex with precision up to Log[z]^4/z^4 . However, the exercise can be continued, getting coefficients a,b,c,d,e in the last formula, then adding one more similar term and so on. *)

Evaluation

The code above gives the expansion of superfunction \(f\) for the base function \(T\!=\!\mathrm{zex}\) in the following form:

\(\!\!\!\!\!\!\!\!\!\!\!\!(6) ~ ~ ~ \displaystyle f(z)= -\frac{1}{z} ~ + \frac{\frac{1}{2}\ell }{ z^2}\) \(\displaystyle ~+ \frac{\frac{-1}{4}\ell^2 +\frac{1}{4}\ell-\frac{1}{6}}{z^3_{\phantom{p}} } ~\) \(\displaystyle ~+ \frac{\frac{ 1}{8}\ell^3 +\frac{-5}{16}\ell^2+\frac{3}{8}\ell+\frac{-7}{48} }{z^4_{\phantom{p}}} ~\) \(\displaystyle ~+ \frac{\frac{-1}{16}\ell^4+\frac{13}{48}\ell^3+\frac{-17}{32}\ell^2+\frac{23}{48}\ell+\frac{-707}{4320} }{z^5_{\phantom{p}}} ~\) \(\displaystyle ~+ \frac{\frac{ 1}{32}\ell^5+\frac{-77}{384}\ell^4+\frac{37}{64}\ell^3+\frac{-83}{96}\ell^2+\frac{1121}{1728}\ell + \frac{-1637}{8640} }{z^6_{\phantom{p}}} ~\) \(\displaystyle ~+ \frac{\frac{-1}{64}\ell^6+\frac{87}{640}\ell^5+\frac{-205}{384}\ell^4+\frac{443}{384}\ell^3+\frac{-1619}{1152}\ell^2+\frac{15427}{17280}\ell + \frac{-274133}{1209600} }{z^6} ~\) \(\displaystyle ~+ O\left(\frac{\ell^7}{z^8}\right) ~\)

where \(\ell\!=\!\ln(\pm z)\). Then, as in the definition, set \(~F_n\!=\!\mathrm{zex}^n\!\Big(f(z\!-\!n)\Big)\).

Case \(~\ell\!=\!\ln(-z)~\)

For \(~\ell\!=\!\ln(-z)~\), let \(x_{4,n}\) be solution of equation \(F_n(x_{4,n})=1\); then

\(\!\!\!\!\!\!\!\!\!\!\!\!\! (8) ~ ~ ~ \mathrm{SuZex}(z) \approx F_n(x_{4,n}\!+\!z)\)

giving approximation of the superfunction of function Zex.

Case \(~\ell\!=\!\ln(z)~\)

For \(~\ell\!=\!\ln(z)~\), equation (6) gives another superfunction, let it be called \(\mathrm{SdZex}\),that approaches the fixed point 0 from below; then

\(\!\!\!\!\!\!\!\!\!\!\!\!\! (9) ~ ~ ~ \mathrm{SdZex}(z) \approx F_n(z_{4,n}\!+\!z)\)

for negative values of \(n\) and approproate \(z_{4,n}\), expression (9) can be considered as approximation of another superfunction of the transfer function Zex.

Several decimal digits of superfunctions can be evaluated using approximations (8) and (9) using calculations with just complex double arithmetics. Similar approach is used in the implementation of the two superfunctions of the exponential to base \(b=\exp^2(-1)=\exp(1/\mathrm e)\approx 1.444667861\) . In that case, the transfer function \(\exp_b\) also has derivative unity at its fixed point \(L=\mathrm e\approx 2.718\)

Keywords

ArcLambertW, Iterate, Regular iteration Superfunction, SuTra, SuZex approximation, Zex,