Difference between revisions of "File:Knesermap.jpg"
| Line 1: | Line 1: | ||
| + | [[Complex map]] of the [[Keneser function]] |
||
| + | |||
| + | \( f=\exp^{1/2} \) |
||
| + | |||
| + | is shown with |
||
| + | |||
| + | lines \( u=\Re(f(z)) = \mathrm{const} \) and |
||
| + | |||
| + | lines \( v=\Im(f(z)) = \mathrm{const} \) |
||
| + | |||
| + | in the complex plane \( z=x+\mathrm i y \) |
||
| + | |||
| + | The [[Keneser function]] \( f \) |
||
| + | is solution of equation |
||
| + | |||
| + | \( f(f(z)) = \exp(z) \) |
||
| + | |||
| + | The [[Kneser function]] is implemented as follows |
||
| + | |||
| + | \( f(z)=\mathrm{tet}(1/2+\mathrm{ate}(z)) \) |
||
| + | |||
| + | where \(\mathrm{tet}\) is natural [[tetration]] and |
||
| + | \(\mathrm{ate}\) is [[arctetration]]. |
||
| + | |||
| + | ==[[C++]] generator of map== |
||
| + | // files [[ado.cin]], [[conto.cin]], [[fsexp.cin]], [[fslog.cin]] should be loaded |
||
| + | <pre> |
||
| + | #include <math.h> |
||
| + | #include <stdio.h> |
||
| + | #include <stdlib.h> |
||
| + | #define DB double |
||
| + | #define DO(x,y) for(x=0;x<y;x++) |
||
| + | using namespace std; |
||
| + | #include<complex> |
||
| + | typedef complex<double> z_type; |
||
| + | // #include <complex.h> |
||
| + | // #define z_type complex<double> |
||
| + | #define Re(x) x.real() |
||
| + | #define Im(x) x.imag() |
||
| + | #define I z_type(0.,1.) |
||
| + | #include "conto.cin" |
||
| + | #include "fsexp.cin" |
||
| + | #include "fslog.cin" |
||
| + | int main(){ int j,k,m,n; DB x,y, p,q, t; z_type z,c,d, cu,cd; |
||
| + | int M=401,M1=M+1; |
||
| + | int N=401,N1=N+1; |
||
| + | DB X[M1],Y[N1], g[M1*N1],f[M1*N1], w[M1*N1]; // w is working array. |
||
| + | char v[M1*N1]; // v is working array |
||
| + | FILE *o; o=fopen("kneserma.eps","w"); ado(o,1620,1620); |
||
| + | fprintf(o,"810 810 translate\n 100 100 scale\n"); |
||
| + | DO(m,M1) X[m]=-8.+.04*(m-.5); |
||
| + | DO(n,N1) Y[n]=-8.+.04*(n-.5); |
||
| + | for(m=-8;m<9;m++) {M(m,-8)L(m,8)} |
||
| + | for(n=-8;n<9;n++) {M( -8,n)L(8,n)} fprintf(o,".006 W 0 0 0 RGB S\n"); |
||
| + | DO(m,M1)DO(n,N1){ g[m*N1+n]=9999; |
||
| + | f[m*N1+n]=9999;} |
||
| + | DO(m,M1){x=X[m]; printf("x=%6.3f\n",x); |
||
| + | DO(n,N1){y=Y[n]; z=z_type(x,y); |
||
| + | c=FSLOG(z); |
||
| + | c=FSEXP(.5+c); |
||
| + | p=Re(c); q=Im(c); |
||
| + | if(p>-9999 && p<9999 && fabs(q)>1.e-12) g[m*N1+n]=p; |
||
| + | if(q>-9999 && q<9999 && fabs(q)>1.e-12) f[m*N1+n]=q; |
||
| + | }} |
||
| + | fprintf(o,"1 setlinejoin 2 setlinecap\n"); |
||
| + | p=2;q=1; |
||
| + | for(m=-3;m<4;m++)for(n=2;n<10;n+=2)conto(o,f,w,v,X,Y,M,N, (m+.1*n),-q,q); |
||
| + | fprintf(o,".014 W 0 .6 0 RGB S\n"); |
||
| + | for(m=0;m<4;m++) for(n=2;n<10;n+=2)conto(o,g,w,v,X,Y,M,N,-(m+.1*n),-q,q); |
||
| + | fprintf(o,".014 W .9 0 0 RGB S\n"); |
||
| + | for(m=0;m<4;m++) for(n=2;n<10;n+=2)conto(o,g,w,v,X,Y,M,N, (m+.1*n),-q,q); |
||
| + | fprintf(o,".014 W 0 0 .9 RGB S\n"); |
||
| + | |||
| + | for(m= 1;m<9;m++) conto(o,f,w,v,X,Y,M,N, (0.-m),-p,p);fprintf(o,".04 W .8 0 0 RGB S\n"); |
||
| + | for(m= 1;m<9;m++) conto(o,f,w,v,X,Y,M,N, (0.+m),-p,p);fprintf(o,".04 W 0 0 .8 RGB S\n"); |
||
| + | conto(o,f,w,v,X,Y,M,N, (0. ),-p,p); fprintf(o,".04 W .5 0 .5 RGB S\n"); |
||
| + | for(m=-8;m<9;m++)conto(o,g,w,v,X,Y,M,N,(0.+m),-p,p);fprintf(o,".04 W 0 0 0 RGB S\n"); |
||
| + | |||
| + | //#include "plofu.cin" |
||
| + | fprintf(o,"0 setlinejoin 0 setlinecap\n"); |
||
| + | |||
| + | x=0.3181315052047641; |
||
| + | y=1.3372357014306895; |
||
| + | M(-8, y)L(x, y) |
||
| + | M(-8,-y)L(x,-y) |
||
| + | fprintf(o,"0 setlinecap 1 1 1 RGB .12 W S\n"); |
||
| + | |||
| + | for(m=0;m<18;m++){M(x-m/2., y)L(x-m/2.-.2, y)} |
||
| + | for(m=0;m<18;m++){M(x-m/2.,-y)L(x-m/2.-.2,-y)} |
||
| + | |||
| + | fprintf(o,"0 setlinecap 0 0 0 RGB .12 W S\n"); |
||
| + | |||
| + | fprintf(o,"showpage\n"); |
||
| + | fprintf(o,"%cTrailer\n",'%'); |
||
| + | fclose(o); |
||
| + | system("epstopdf kneserma.eps"); |
||
| + | system( "open kneserma.pdf"); //for macintosh |
||
| + | getchar(); system("killall Preview"); // For macintosh |
||
| + | } |
||
| + | </pre> |
||
| + | |||
| + | ==[[Latex]] generator of labels== |
||
| + | % kneserma.pdf should be already generated with the code above |
||
| + | |||
| + | <pre> |
||
| + | \documentclass[12pt]{article} |
||
| + | \usepackage{geometry} |
||
| + | \paperwidth 1700pt |
||
| + | \paperheight 1674pt |
||
| + | \textheight 1800pt |
||
| + | \textwidth 1800pt |
||
| + | \topmargin -88pt |
||
| + | \oddsidemargin -72pt |
||
| + | \usepackage{graphics} |
||
| + | \newcommand \sx {\scalebox} |
||
| + | \newcommand \ing {\includegraphics} |
||
| + | \usepackage{rotating} |
||
| + | \newcommand \rot {\begin{turn}} |
||
| + | \newcommand \ero {\end{turn}} |
||
| + | \pagestyle{empty} |
||
| + | \parindent 0pt |
||
| + | \begin{document} |
||
| + | \huge |
||
| + | \begin{picture}(1620,1620) |
||
| + | \put(80,20){\ing{kneserma}} |
||
| + | \put(40,1606){\sx{3}{$y$}} |
||
| + | \put(40,1410){\sx{3}{$6$}} |
||
| + | \put(40,1210){\sx{3}{$4$}} |
||
| + | \put(40,1010){\sx{3}{$2$}} |
||
| + | %\put(20,960){\sx{2.7}{$y_0$}} |
||
| + | \put(40,810){\sx{3}{$0$}} |
||
| + | %\put(-18,690){\sx{2.6}{$-y_0$}} |
||
| + | \put(-14,610){\sx{3}{$-2$}} |
||
| + | \put(-14,410){\sx{3}{$-4$}} |
||
| + | \put(-14,210){\sx{3}{$-6$}} |
||
| + | \put(-14,10){\sx{3}{$-8$}} |
||
| + | \put(24,-28){\sx{3}{$-8$}} |
||
| + | \put(224,-28){\sx{3}{$-6$}} |
||
| + | \put(424,-28){\sx{3}{$-4$}} |
||
| + | \put(624,-28){\sx{3}{$-2$}} |
||
| + | \put(880,-28){\sx{3}{$0$}} |
||
| + | \put(1080,-28){\sx{3}{$2$}} |
||
| + | \put(1280,-28){\sx{3}{$4$}} |
||
| + | \put(1480,-28){\sx{3}{$6$}} |
||
| + | \put(1660,-26){\sx{3.2}{$x$}} |
||
| + | |||
| + | \put(1480,1460){\sx{2.7}{\rot{18}$u=-8$\ero}} |
||
| + | \put(1550,1250){\sx{2.7}{\rot{30}$u=8$\ero}} |
||
| + | |||
| + | \put(1542,952){\sx{2.7}{\rot{-13}$v=8$\ero}} |
||
| + | \put(1496,670){\sx{2.7}{\rot{11}$v=-8$\ero}} |
||
| + | |||
| + | \put(1552,394){\sx{2.7}{\rot{-34}$u=8$\ero}} |
||
| + | \put(1480,174){\sx{2.7}{\rot{-20}$u=-8$\ero}} |
||
| + | |||
| + | \end{picture} |
||
| + | \end{document} |
||
| + | </pre> |
||
| + | |||
| + | ==References== |
||
| + | <references/> |
||
| + | http://www.digizeitschriften.de/dms/img/?PID=GDZPPN002175851&physid=phys63#navi |
||
| + | [[Hellmuth Kneser]]. Reelle analytische Lösungen der Gleichung \( \varphi(\varphi(x))=\mathrm e^x \) und verwandter Funktionalgleichungen. |
||
| + | Journal für die reine und angewandte Mathematik / Zeitschriftenband (1950) / Artikel / 56 - 67 |
||
| + | |||
| + | http://www.ils.uec.ac.jp/~dima/PAPERS/2009analuxpRepri.pdf |
||
| + | http://www.ams.org/mcom/2009-78-267/S0025-5718-09-02188-7/home.html |
||
| + | D.Kouznetsov. (2009). Solutions of F(z+1)=exp(F(z)) in the complex plane. Mathematics of Computation, 78: 1647-1670. DOI:10.1090/S0025-5718-09-02188-7 |
||
| + | |||
| + | http://www.ils.uec.ac.jp/~dima/PAPERS/2010vladie.pdf D.Kouznetsov. Superexponential as special function. Vladikavkaz Mathematical Journal, 2010, v.12, issue 2, p.31-45 |
||
| + | |||
| + | http://www.ils.uec.ac.jp/~dima/PAPERS/2009supefae.pdf D.Kouznetsov, H.Trappmann. Superfunctions and sqrt of Factorial. (2010) |
||
| + | |||
| + | http://journal.kkms.org/index.php/kjm/article/view/428 William Paulsen. Finding the natural solution to f(f(x))=exp(x). Korean J. Math. Vol 24, No 1 (2016) pp.81-106. |
||
| + | |||
| + | https://link.springer.com/article/10.1007/s10444-017-9524-1 William Paulsen, Samuel Cowgill. Solving F(z + 1) = b ^ F(z) in the complex plane. Advances in Computational Mathematics, December 2017, Volume 43, Issue 6, pp 1261–1282 |
||
Revision as of 18:03, 31 December 2019
Complex map of the Keneser function
\( f=\exp^{1/2} \)
is shown with
lines \( u=\Re(f(z)) = \mathrm{const} \) and
lines \( v=\Im(f(z)) = \mathrm{const} \)
in the complex plane \( z=x+\mathrm i y \)
The Keneser function \( f \) is solution of equation
\( f(f(z)) = \exp(z) \)
The Kneser function is implemented as follows
\( f(z)=\mathrm{tet}(1/2+\mathrm{ate}(z)) \)
where \(\mathrm{tet}\) is natural tetration and \(\mathrm{ate}\) is arctetration.
C++ generator of map
// files ado.cin, conto.cin, fsexp.cin, fslog.cin should be loaded
#include <math.h>
#include <stdio.h>
#include <stdlib.h>
#define DB double
#define DO(x,y) for(x=0;x<y;x++)
using namespace std;
#include<complex>
typedef complex<double> z_type;
// #include <complex.h>
// #define z_type complex<double>
#define Re(x) x.real()
#define Im(x) x.imag()
#define I z_type(0.,1.)
#include "conto.cin"
#include "fsexp.cin"
#include "fslog.cin"
int main(){ int j,k,m,n; DB x,y, p,q, t; z_type z,c,d, cu,cd;
int M=401,M1=M+1;
int N=401,N1=N+1;
DB X[M1],Y[N1], g[M1*N1],f[M1*N1], w[M1*N1]; // w is working array.
char v[M1*N1]; // v is working array
FILE *o; o=fopen("kneserma.eps","w"); ado(o,1620,1620);
fprintf(o,"810 810 translate\n 100 100 scale\n");
DO(m,M1) X[m]=-8.+.04*(m-.5);
DO(n,N1) Y[n]=-8.+.04*(n-.5);
for(m=-8;m<9;m++) {M(m,-8)L(m,8)}
for(n=-8;n<9;n++) {M( -8,n)L(8,n)} fprintf(o,".006 W 0 0 0 RGB S\n");
DO(m,M1)DO(n,N1){ g[m*N1+n]=9999;
f[m*N1+n]=9999;}
DO(m,M1){x=X[m]; printf("x=%6.3f\n",x);
DO(n,N1){y=Y[n]; z=z_type(x,y);
c=FSLOG(z);
c=FSEXP(.5+c);
p=Re(c); q=Im(c);
if(p>-9999 && p<9999 && fabs(q)>1.e-12) g[m*N1+n]=p;
if(q>-9999 && q<9999 && fabs(q)>1.e-12) f[m*N1+n]=q;
}}
fprintf(o,"1 setlinejoin 2 setlinecap\n");
p=2;q=1;
for(m=-3;m<4;m++)for(n=2;n<10;n+=2)conto(o,f,w,v,X,Y,M,N, (m+.1*n),-q,q);
fprintf(o,".014 W 0 .6 0 RGB S\n");
for(m=0;m<4;m++) for(n=2;n<10;n+=2)conto(o,g,w,v,X,Y,M,N,-(m+.1*n),-q,q);
fprintf(o,".014 W .9 0 0 RGB S\n");
for(m=0;m<4;m++) for(n=2;n<10;n+=2)conto(o,g,w,v,X,Y,M,N, (m+.1*n),-q,q);
fprintf(o,".014 W 0 0 .9 RGB S\n");
for(m= 1;m<9;m++) conto(o,f,w,v,X,Y,M,N, (0.-m),-p,p);fprintf(o,".04 W .8 0 0 RGB S\n");
for(m= 1;m<9;m++) conto(o,f,w,v,X,Y,M,N, (0.+m),-p,p);fprintf(o,".04 W 0 0 .8 RGB S\n");
conto(o,f,w,v,X,Y,M,N, (0. ),-p,p); fprintf(o,".04 W .5 0 .5 RGB S\n");
for(m=-8;m<9;m++)conto(o,g,w,v,X,Y,M,N,(0.+m),-p,p);fprintf(o,".04 W 0 0 0 RGB S\n");
//#include "plofu.cin"
fprintf(o,"0 setlinejoin 0 setlinecap\n");
x=0.3181315052047641;
y=1.3372357014306895;
M(-8, y)L(x, y)
M(-8,-y)L(x,-y)
fprintf(o,"0 setlinecap 1 1 1 RGB .12 W S\n");
for(m=0;m<18;m++){M(x-m/2., y)L(x-m/2.-.2, y)}
for(m=0;m<18;m++){M(x-m/2.,-y)L(x-m/2.-.2,-y)}
fprintf(o,"0 setlinecap 0 0 0 RGB .12 W S\n");
fprintf(o,"showpage\n");
fprintf(o,"%cTrailer\n",'%');
fclose(o);
system("epstopdf kneserma.eps");
system( "open kneserma.pdf"); //for macintosh
getchar(); system("killall Preview"); // For macintosh
}
Latex generator of labels
% kneserma.pdf should be already generated with the code above
\documentclass[12pt]{article}
\usepackage{geometry}
\paperwidth 1700pt
\paperheight 1674pt
\textheight 1800pt
\textwidth 1800pt
\topmargin -88pt
\oddsidemargin -72pt
\usepackage{graphics}
\newcommand \sx {\scalebox}
\newcommand \ing {\includegraphics}
\usepackage{rotating}
\newcommand \rot {\begin{turn}}
\newcommand \ero {\end{turn}}
\pagestyle{empty}
\parindent 0pt
\begin{document}
\huge
\begin{picture}(1620,1620)
\put(80,20){\ing{kneserma}}
\put(40,1606){\sx{3}{$y$}}
\put(40,1410){\sx{3}{$6$}}
\put(40,1210){\sx{3}{$4$}}
\put(40,1010){\sx{3}{$2$}}
%\put(20,960){\sx{2.7}{$y_0$}}
\put(40,810){\sx{3}{$0$}}
%\put(-18,690){\sx{2.6}{$-y_0$}}
\put(-14,610){\sx{3}{$-2$}}
\put(-14,410){\sx{3}{$-4$}}
\put(-14,210){\sx{3}{$-6$}}
\put(-14,10){\sx{3}{$-8$}}
\put(24,-28){\sx{3}{$-8$}}
\put(224,-28){\sx{3}{$-6$}}
\put(424,-28){\sx{3}{$-4$}}
\put(624,-28){\sx{3}{$-2$}}
\put(880,-28){\sx{3}{$0$}}
\put(1080,-28){\sx{3}{$2$}}
\put(1280,-28){\sx{3}{$4$}}
\put(1480,-28){\sx{3}{$6$}}
\put(1660,-26){\sx{3.2}{$x$}}
\put(1480,1460){\sx{2.7}{\rot{18}$u=-8$\ero}}
\put(1550,1250){\sx{2.7}{\rot{30}$u=8$\ero}}
\put(1542,952){\sx{2.7}{\rot{-13}$v=8$\ero}}
\put(1496,670){\sx{2.7}{\rot{11}$v=-8$\ero}}
\put(1552,394){\sx{2.7}{\rot{-34}$u=8$\ero}}
\put(1480,174){\sx{2.7}{\rot{-20}$u=-8$\ero}}
\end{picture}
\end{document}
References
http://www.digizeitschriften.de/dms/img/?PID=GDZPPN002175851&physid=phys63#navi Hellmuth Kneser. Reelle analytische Lösungen der Gleichung \( \varphi(\varphi(x))=\mathrm e^x \) und verwandter Funktionalgleichungen. Journal für die reine und angewandte Mathematik / Zeitschriftenband (1950) / Artikel / 56 - 67
http://www.ils.uec.ac.jp/~dima/PAPERS/2009analuxpRepri.pdf http://www.ams.org/mcom/2009-78-267/S0025-5718-09-02188-7/home.html D.Kouznetsov. (2009). Solutions of F(z+1)=exp(F(z)) in the complex plane. Mathematics of Computation, 78: 1647-1670. DOI:10.1090/S0025-5718-09-02188-7
http://www.ils.uec.ac.jp/~dima/PAPERS/2010vladie.pdf D.Kouznetsov. Superexponential as special function. Vladikavkaz Mathematical Journal, 2010, v.12, issue 2, p.31-45
http://www.ils.uec.ac.jp/~dima/PAPERS/2009supefae.pdf D.Kouznetsov, H.Trappmann. Superfunctions and sqrt of Factorial. (2010)
http://journal.kkms.org/index.php/kjm/article/view/428 William Paulsen. Finding the natural solution to f(f(x))=exp(x). Korean J. Math. Vol 24, No 1 (2016) pp.81-106.
https://link.springer.com/article/10.1007/s10444-017-9524-1 William Paulsen, Samuel Cowgill. Solving F(z + 1) = b ^ F(z) in the complex plane. Advances in Computational Mathematics, December 2017, Volume 43, Issue 6, pp 1261–1282
File history
Click on a date/time to view the file as it appeared at that time.
| Date/Time | Thumbnail | Dimensions | User | Comment | |
|---|---|---|---|---|---|
| current | 18:03, 31 December 2019 | 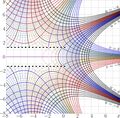 | 2,352 × 2,316 (1.55 MB) | T (talk | contribs) |
You cannot overwrite this file.
File usage
The following page uses this file: