Difference between revisions of "Tetration to Sheldon base"
| (6 intermediate revisions by 2 users not shown) | |||
| Line 1: | Line 1: | ||
| + | <div style="float:right;width:477px"> |
||
| ⚫ | |||
| + | <div style="width:500px"> |
||
| ⚫ | |||
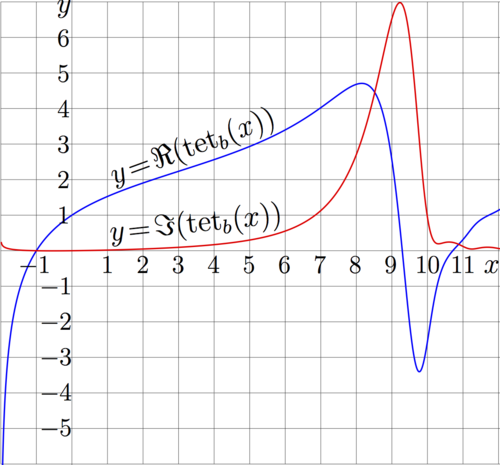
| + | [[File:Shelre60.png|500px]]<small> Explicit plot of real and imaginary parts of tetration to base \(b\!=\!s\)</small> |
||
| ⚫ | |||
| + | |||
| ⚫ | |||
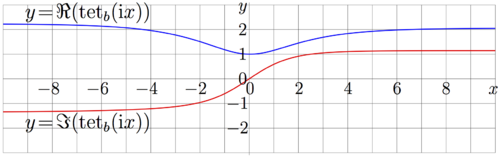
| + | [[File:Shelima600.png|500px]]<small>Distribution of tetration to \(b\!=\!s\) along the imaginary axis</small> |
||
| ⚫ | |||
| + | |||
| ⚫ | |||
| ⚫ | |||
| ⚫ | |||
| ⚫ | |||
| + | </div></div> |
||
| + | |||
| ⚫ | |||
| + | |||
| ⚫ | |||
| + | |||
| ⚫ | |||
Yet, no specific definition for the Sheldon number is available; |
Yet, no specific definition for the Sheldon number is available; |
||
| − | the only observation |
+ | the only observation, that [[Sheldon Levenstein]] somehow had believed that the [[tetration]] to such a base is very difficult to evaluate |
<ref name="privatec"> |
<ref name="privatec"> |
||
Sheldon Levenstein. Tetration for e^(1/e) branch point. |
Sheldon Levenstein. Tetration for e^(1/e) branch point. |
||
| Line 19: | Line 29: | ||
bigger than the nearest base that is only the Shell Thron boundary.</i> |
bigger than the nearest base that is only the Shell Thron boundary.</i> |
||
</ref> with his algorithm of "merging of solution" <ref name="sheldon"> |
</ref> with his algorithm of "merging of solution" <ref name="sheldon"> |
||
| − | + | https://math.eretrandre.org/tetrationforum/showthread.php?tid=729 |
|
Sheldon Levenson. Complex base tetration program. [[Tetration and Related Topics]], 2012 March 1. |
Sheldon Levenson. Complex base tetration program. [[Tetration and Related Topics]], 2012 March 1. |
||
</ref>. |
</ref>. |
||
| + | In such a way, the constant \(s\) above can be qualified as "exact". |
||
Following the general ideology of [[TORI]], the solutions that are believed not to exist (or to be extremely difficult to evaluate) are of special interest. |
Following the general ideology of [[TORI]], the solutions that are believed not to exist (or to be extremely difficult to evaluate) are of special interest. |
||
| − | For this reason, tetration to the Sheldon base is described in this article |
+ | For this reason, tetration to the Sheldon base is described in this article and in the book [[Superfunctions]] |
| + | <ref> |
||
| + | https://www.ils.uec.ac.jp/~dima/BOOK/443.pdf <br> |
||
| + | https://mizugadro.mydns.jp/BOOK/444.pdf |
||
| + | D.Kouznetsov. Superfunctions. 2020 |
||
| + | </ref>. |
||
==Fixed points of log<sub>s</sub> and properties of tet<sub>s</sub>== |
==Fixed points of log<sub>s</sub> and properties of tet<sub>s</sub>== |
||
| − | According to the general expectations about [[tetration]] |
+ | According to the general expectations about [[tetration]] \(\mathrm{tet}_s\), it satisfies the [[transfer equation]]: |
| − | : |
+ | : \(\!\!\!\!\!\!\!\! (1) \displaystyle ~ ~ ~ \exp(a~ \mathrm{tet_s}(z)) = \mathrm{tet}_s(z\!+\!1)\) |
| − | where |
+ | where \(a=\ln(b)\approx \) \(0.4227073870410604 + 0.0116910660021443~ i\) |
with the additional condition |
with the additional condition |
||
| − | : |
+ | : \(\!\!\!\!\!\!\!\! (2) \displaystyle ~ ~ ~ \mathrm{tet_s}(0)=1\) |
and the asimptitic behavior determined with function [[Filog]] : |
and the asimptitic behavior determined with function [[Filog]] : |
||
| − | : |
+ | : \(\!\!\!\!\!\!\!\! (3) \displaystyle ~ ~ ~ \lim_{y \rightarrow +\infty} \mathrm{tet_s}(x+\mathrm i y)=\) \(L_1 =\) \(\mathrm{Filog}(a)\approx 2.0565398441043761 +1.1445267140098765~ i\) |
| − | : |
+ | : \(\!\!\!\!\!\!\!\! (4) \displaystyle ~ ~ ~ \lim_{y \rightarrow -\infty} \mathrm{tet_s}(x+\mathrm i y)=\) \(L_2=\) \(\mathrm{Filog}(a^*)^*\approx 2.2284359658711805 -1.3507994961102865~ i\) |
| − | In addition, |
+ | In addition, \(\mathrm{tet}_s(z)\) is supposed to be holomorphic at least for \(z>-2\), and also in the left hand side of the complex half-line, except some facility of the negative part of the real axis \(z<-2\); the tetration should have the cutline there. |
| − | In the upper half-plane, the tetration should behave as |
+ | In the upper half-plane, the tetration should behave as \(L_1+\exp(k_1 (z-z_1)) + O(\exp(2 k_1 (z-z_1))\);<br> |
| − | In the lower half-plane, the tetration should behave as |
+ | In the lower half-plane, the tetration should behave as \(L_2+\exp(k_2 (z-z_1)) + O(\exp(2 k_2 (z-z_2))\); |
| − | for some complex constants |
+ | for some complex constants \(z_1\) and \(z_2\), at |
| − | + | \(~k_1 =\ln(L_1 a) ~\) and |
|
| − | + | \(~k_2 =\ln(L_2 a) ~\). |
|
| − | For the [[Sheldon base]], the increments |
+ | For the [[Sheldon base]], the increments \(k_1\) and \(k_2\) are evaluated as |
| − | : |
+ | : \(k_1 =\ln(L_1 a) \approx\) \( -0.0047589243931785 + 0.5354935770338939~ i\) |
| − | : |
+ | : \(k_2 =\ln(L_2 a) \approx\) \(0.0970758595007548 - 0.517289596155984~i\) |
The quasiperiod in the upper half-plane |
The quasiperiod in the upper half-plane |
||
| − | : |
+ | : \(T_1= ~ 2 \pi \mathrm i/k_1 \approx\) \( -0.1042667514229599~i + 11.7325200133916496~ \) |
and that in the lower half-plane is |
and that in the lower half-plane is |
||
| − | : |
+ | : \(T_2=- 2 \pi \mathrm i/k_2 \approx \) \( -2.2018723603861230~i + 11.7331504449085493~ \) |
| − | These quasi-periods are used to arrange the labels at the [[complex map]] of the tetration with the [[multiput]] command; in the upper half-plane the increment is |
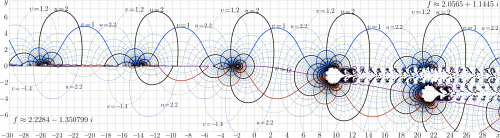
+ | These quasi-periods are used to arrange the labels at the [[complex map]] of the tetration with the [[multiput]] command; in the upper half-plane the increment is \(T_1\), and in the lower half-plane, it is \(T_2\). |
| − | The properties above give the simple and efficient way of the precise evaluation of |
+ | The properties above give the simple and efficient way of the precise evaluation of \(\mathrm{tet}_s\) through the Cauchi integral equation <ref name="moc1"> |
| − | + | https://www.ams.org/mcom/2009-78-267/S0025-5718-09-02188-7/home.html D.Kouznetsov. (2009). Solutions of \(F(z+1)=\exp(F(z))\) in the complex plane.. Mathematics of Computation, 78: 1647-1670.</ref>. |
|
==References== |
==References== |
||
| Line 65: | Line 81: | ||
[[Category:Tetration]] |
[[Category:Tetration]] |
||
[[Category:Superfunction]] |
[[Category:Superfunction]] |
||
| + | [[Category:Tetration to Sheldon base]] |
||
[[Category:Sheldon Levenstein]] |
[[Category:Sheldon Levenstein]] |
||
[[Category:Articles in English]] |
[[Category:Articles in English]] |
||
Latest revision as of 21:33, 13 July 2020
Tetration to Sheldon base refers to the specific case of tetration to the complex base \(b=s\), where
\( s=1.52598338517 + 0.0178411853321~ {i}\).
is the Sheldon number. In such a way, it is holomorphic function \(\mathrm{tet}_s\).
Yet, no specific definition for the Sheldon number is available; the only observation, that Sheldon Levenstein somehow had believed that the tetration to such a base is very difficult to evaluate [1] with his algorithm of "merging of solution" [2].
In such a way, the constant \(s\) above can be qualified as "exact". Following the general ideology of TORI, the solutions that are believed not to exist (or to be extremely difficult to evaluate) are of special interest. For this reason, tetration to the Sheldon base is described in this article and in the book Superfunctions [3].
Fixed points of logs and properties of tets
According to the general expectations about tetration \(\mathrm{tet}_s\), it satisfies the transfer equation:
- \(\!\!\!\!\!\!\!\! (1) \displaystyle ~ ~ ~ \exp(a~ \mathrm{tet_s}(z)) = \mathrm{tet}_s(z\!+\!1)\)
where \(a=\ln(b)\approx \) \(0.4227073870410604 + 0.0116910660021443~ i\) with the additional condition
- \(\!\!\!\!\!\!\!\! (2) \displaystyle ~ ~ ~ \mathrm{tet_s}(0)=1\)
and the asimptitic behavior determined with function Filog :
- \(\!\!\!\!\!\!\!\! (3) \displaystyle ~ ~ ~ \lim_{y \rightarrow +\infty} \mathrm{tet_s}(x+\mathrm i y)=\) \(L_1 =\) \(\mathrm{Filog}(a)\approx 2.0565398441043761 +1.1445267140098765~ i\)
- \(\!\!\!\!\!\!\!\! (4) \displaystyle ~ ~ ~ \lim_{y \rightarrow -\infty} \mathrm{tet_s}(x+\mathrm i y)=\) \(L_2=\) \(\mathrm{Filog}(a^*)^*\approx 2.2284359658711805 -1.3507994961102865~ i\)
In addition, \(\mathrm{tet}_s(z)\) is supposed to be holomorphic at least for \(z>-2\), and also in the left hand side of the complex half-line, except some facility of the negative part of the real axis \(z<-2\); the tetration should have the cutline there.
In the upper half-plane, the tetration should behave as \(L_1+\exp(k_1 (z-z_1)) + O(\exp(2 k_1 (z-z_1))\);
In the lower half-plane, the tetration should behave as \(L_2+\exp(k_2 (z-z_1)) + O(\exp(2 k_2 (z-z_2))\);
for some complex constants \(z_1\) and \(z_2\), at
\(~k_1 =\ln(L_1 a) ~\) and
\(~k_2 =\ln(L_2 a) ~\).
For the Sheldon base, the increments \(k_1\) and \(k_2\) are evaluated as
- \(k_1 =\ln(L_1 a) \approx\) \( -0.0047589243931785 + 0.5354935770338939~ i\)
- \(k_2 =\ln(L_2 a) \approx\) \(0.0970758595007548 - 0.517289596155984~i\)
The quasiperiod in the upper half-plane
- \(T_1= ~ 2 \pi \mathrm i/k_1 \approx\) \( -0.1042667514229599~i + 11.7325200133916496~ \)
and that in the lower half-plane is
- \(T_2=- 2 \pi \mathrm i/k_2 \approx \) \( -2.2018723603861230~i + 11.7331504449085493~ \)
These quasi-periods are used to arrange the labels at the complex map of the tetration with the multiput command; in the upper half-plane the increment is \(T_1\), and in the lower half-plane, it is \(T_2\).
The properties above give the simple and efficient way of the precise evaluation of \(\mathrm{tet}_s\) through the Cauchi integral equation [4].
References
- ↑ Sheldon Levenstein. Tetration for e^(1/e) branch point. Sun, 19 Feb 2012 06:20:26 -0600. .. I don't have a working generic algorithm for any generic complex base, especially one near the Shell Thron boundary. For example, consider the superfunction developed from the attracting fixed point, where sexp_b(1), for an arbitrary complex base b inside the Shell Thron boundary, For a specific case, consider b=1.52598338517 + 0.0178411853321~ i. This imaginary component of this base is about 10% bigger than the nearest base that is only the Shell Thron boundary.
- ↑ https://math.eretrandre.org/tetrationforum/showthread.php?tid=729 Sheldon Levenson. Complex base tetration program. Tetration and Related Topics, 2012 March 1.
- ↑
https://www.ils.uec.ac.jp/~dima/BOOK/443.pdf
https://mizugadro.mydns.jp/BOOK/444.pdf D.Kouznetsov. Superfunctions. 2020 - ↑ https://www.ams.org/mcom/2009-78-267/S0025-5718-09-02188-7/home.html D.Kouznetsov. (2009). Solutions of \(F(z+1)=\exp(F(z))\) in the complex plane.. Mathematics of Computation, 78: 1647-1670.
Keywords
Tetration, superfunction, transfer equation, Sheldon Levenstein