Difference between revisions of "File:Tetreal10bx10d.png"
(Importing image file) |
|||
| Line 1: | Line 1: | ||
| + | Plot of [[Tetration]]: $y=\mathrm{tet}_b(x)$ versus $x$ for |
||
| − | Importing image file |
||
| + | : $b \rightarrow 1$, |
||
| + | : $b = 1.1$, |
||
| + | : $b = 1.2$, |
||
| + | : $b = 1.3$, |
||
| + | : $b = 1.4$, |
||
| + | : $b = \sqrt{2}\approx 1.41,$ |
||
| + | : $b = \exp(1/ \mathrm e) \approx 1.44,$ |
||
| + | : $b = 1.5$, |
||
| + | : $b = 1.6$, |
||
| + | : $b = 1.7$, |
||
| + | : $b = 1.8$, |
||
| + | : $b = 1.9$, |
||
| + | : $b = 2$, |
||
| + | : $b = \mathrm e \approx 2.71$, |
||
| + | : $b = 10$, |
||
| + | : $b \rightarrow \infty$. |
||
| + | |||
| + | Improved version of the previous pit |
||
| + | |||
| + | Copyleft 2010 by Dmitrii Kouznetsov: |
||
| + | Please attribute the source at the reuse: it helps to trace errors if any |
||
| + | |||
| + | ==[[C++]] generator of curves== |
||
| + | |||
| + | // Files [[GLxw2048.inc]], [[f2048ten.inc]], [[f4ten.cin]], [[fit1.cin]] should be loaded to the working directory in order to compile the [[C++]] code below: |
||
| + | |||
| + | #include <math.h> |
||
| + | #include <stdio.h> |
||
| + | #include <stdlib.h> |
||
| + | #define DB double |
||
| + | #define DO(x,y) for(x=0;x<y;x++) |
||
| + | using namespace std; |
||
| + | #include <complex> |
||
| + | typedef complex<double> z_type; |
||
| + | #define Re(x) x.real() |
||
| + | #define Im(x) x.imag() |
||
| + | #define I z_type(0.,1.) |
||
| + | |||
| + | //b=10 |
||
| + | #include "f4ten.cin" |
||
| + | |||
| + | #include "fit1.cin" |
||
| + | |||
| + | void ado(FILE *O, int X, int Y) |
||
| + | { fprintf(O,"%c!PS-Adobe-2.0 EPSF-2.0\n",'%'); |
||
| + | fprintf(O,"%c%cBoundingBox: 0 0 %d %d\n",'%','%',X,Y); |
||
| + | fprintf(O,"/M {moveto} bind def\n"); |
||
| + | fprintf(O,"/L {lineto} bind def\n"); |
||
| + | fprintf(O,"/S {stroke} bind def\n"); |
||
| + | fprintf(O,"/s {show newpath} bind def\n"); |
||
| + | fprintf(O,"/C {closepath} bind def\n"); |
||
| + | fprintf(O,"/F {fill} bind def\n"); |
||
| + | fprintf(O,"/o {.1 0 360 arc C S} bind def\n"); |
||
| + | fprintf(O,"/times-Roman findfont 20 scalefont setfont\n"); |
||
| + | fprintf(O,"/W {setlinewidth} bind def\n"); |
||
| + | fprintf(O,"/RGB {setrgbcolor} bind def\n");} |
||
| + | //#include "ado.cin" |
||
| + | |||
| + | #define M(x,y) fprintf(o,"%6.4f %6.4f M\n",0.+x,0.+y); |
||
| + | #define L(x,y) fprintf(o,"%6.4f %6.4f L\n",0.+x,0.+y); |
||
| + | #define o(x,y) fprintf(o,"%6.4f %6.4f o\n",0.+x,0.+y); |
||
| + | |||
| + | main(){ int j,k,m,n; DB p,q,t1,t3,u,v,w,x,y; z_type z,c,d; |
||
| + | FILE *o;o=fopen("tet10bx.eps","w");ado(o,134,124); |
||
| + | fprintf(o,"22 22 translate\n 10 10 scale\n"); |
||
| + | fprintf(o,"2 setlinecap\n"); |
||
| + | for(m=-2;m<12;m++){if(m!=0){M(m,-2)L(m,10)}} |
||
| + | for(n= -2;n<11;n++){if(n!=0){M(-2,n)L(11,n)}} fprintf(o,".006 W 0 0 0 RGB S\n"); |
||
| + | M(-2,0)L(11.1,0) M(0, -2)L(0,10.1) fprintf(o,".03 W 0 0 0 RGB S\n"); |
||
| + | M(0,M_E)L(11.,M_E) fprintf(o,".006 W 0 0 0 RGB S\n"); |
||
| + | fprintf(o,"1 setlinejoin 1 setlinecap\n"); |
||
| + | |||
| + | //DO(m,400){x=-1.99+.008*m;y=Re(FIT1(log(10.),x)); if(y>10.3) break; if(m==0)M(x,y)else L(x,y)} fprintf(o,".03 W .5 0 .5 RGB S\n"); |
||
| + | DO(m,400){x=-1.80+.02*m; y=Re(FIT1(log(2.),x)); if(y>10.3) break; if(m==0)M(x,y)else L(x,y)} fprintf(o,".03 W .5 0 .5 RGB S\n"); |
||
| + | DO(m,400){x=-1.78+.02*m; y=Re(FIT1(log(1.9),x)); if(y>10.33) break; if(m==0)M(x,y)else L(x,y)} fprintf(o,".02 W 0 .5 0 RGB S\n"); |
||
| + | DO(m,400){x=-1.77+.02*m; y=Re(FIT1(log(1.8),x)); if(y>10.33) break; if(m==0)M(x,y)else L(x,y)} fprintf(o,".02 W 0 .5 0 RGB S\n"); |
||
| + | DO(m,400){x=-1.74+.02*m; y=Re(FIT1(log(1.7),x)); if(y>10.3) break; if(m==0)M(x,y)else L(x,y)} fprintf(o,".02 W 0 .5 0 RGB S\n"); |
||
| + | DO(m,400){x=-1.72+.03*m; y=Re(FIT1(log(1.6),x)); if(y>10.3) break; if(m==0)M(x,y)else L(x,y)} fprintf(o,".02 W 0 .5 0 RGB S\n"); |
||
| + | DO(m,400){x=-1.68+.04*m; y=Re(FIT1(log(1.5),x)); if(y>10.3) break; if(m==0)M(x,y)else L(x,y)} fprintf(o,".02 W 0 .5 0 RGB S\n"); |
||
| + | DO(m,400){x=-1.64+.04*m; y=Re(FIT1(log(1.4),x)); if(x>11.1) break; if(m==0)M(x,y)else L(x,y)} fprintf(o,".02 W 0 .5 0 RGB S\n"); |
||
| + | DO(m,400){x=-1.58+.04*m; y=Re(FIT1(log(1.3),x)); if(x>11.1) break; if(m==0)M(x,y)else L(x,y)} fprintf(o,".02 W 0 .5 0 RGB S\n"); |
||
| + | DO(m,400){x=-1.52+.04*m; y=Re(FIT1(log(1.2),x)); if(x>11.1) break; if(m==0)M(x,y)else L(x,y)} fprintf(o,".02 W 0 .5 0 RGB S\n"); |
||
| + | DO(m,400){x=-1.42+.04*m; y=Re(FIT1(log(1.1),x)); if(x>11.1) break; if(m==0)M(x,y)else L(x,y)} fprintf(o,".02 W 0 .5 0 RGB S\n"); |
||
| + | // |
||
| + | DO(m,400){x=-1.65+.04*m; y=Re(FIT1(1./M_E,x)); if(x>11.1) break; if(m==0)M(x,y)else L(x,y)} fprintf(o,".03 W 0 0 .7 RGB S\n"); |
||
| + | DO(m,400){x=-1.64+.04*m; y=Re(FIT1(log(sqrt(2.)),x)); if(x>11.1) break; if(m==0)M(x,y)else L(x,y)} fprintf(o,".03 W .8 0 0 RGB S\n"); |
||
| + | DO(m,400){x=-1.873+.01*m; y=Re(FIT1(1.,x)); if(y>11) break; if(m==0)M(x,y)else L(x,y)} fprintf(o,".02 W 0 0 0 RGB S\n"); |
||
| + | // |
||
| + | DO(m,401){x=-1.987+.01*m;y=Re(F4TEN(x));if(m==0)M(x,y)else L(x,y)}fprintf(o,".02 W .5 0 .5 RGB S\n"); |
||
| + | //DO(m,39){x=-1.89+.098*m; y=Re(FSEXP(x));if(m==0)M(x,y)else L(x,y)} fprintf(o,".01 W 0 0 0 RGB S\n"); |
||
| + | //DO(m,48){x=-1.82+.0973*m; y=Re(F2(x)); if(m==0)M(x,y)else L(x,y)} fprintf(o,".01 W 0 0 0 RGB S\n"); |
||
| + | //DO(m,126){x=-1.72+.1*m; y=Re(F15(x)); if(m==0)M(x,y)else L(x,y)} fprintf(o,".01 W 0 0 0 RGB S\n"); |
||
| + | //DO(m,130){x=-1.65+.1*m; y=Re(E1ETF(x)); if(m==0)M(x,y)else L(x,y)} fprintf(o,".01 W 0 0 0 RGB S\n"); |
||
| + | //DO(m,130){x=-1.64+.1*m; y=Re(f21E(x)); if(m==0)M(x,y)else L(x,y)} fprintf(o,".01 W 0 0 0 RGB S\n"); |
||
| + | M(-1.998,-2)L(-1.992,-.01)L(-1,0)L(-.01,.01)L(0,1)L(.012,10.1) fprintf(o,".02 W .4 0 .8 RGB S\n"); |
||
| + | M(-1.01,-2)L(-1,0)L(-.99,.99)L(0,1)L(10.97,1.01) fprintf(o,".02 W .2 .4 0 RGB S\n"); |
||
| + | fprintf(o,"showpage\n%cTrailer",'%'); fclose(o); |
||
| + | system("epstopdf tet10bx.eps"); |
||
| + | system( "open tet10bx.pdf"); //mac |
||
| + | // system( "xpdf tet10bx.pdf"); // linux |
||
| + | getchar(); system("killall Preview");// mac |
||
| + | } |
||
| + | |||
| + | ==[[Latex]] generator of curves== |
||
| + | |||
| + | % File [[tet10bx.pdf]] sould be generated with code above in order to compile the [[Latex]] document below % <br> |
||
| + | %<nowiki> |
||
| + | \documentclass[12pt]{article} % <br> |
||
| + | \usepackage{geometry} % See geometry.pdf % <br> |
||
| + | \geometry{letterpaper} % ... or a4paper or a5paper or ... ??% <br> |
||
| + | \usepackage{graphicx}% <br> |
||
| + | \usepackage{amssymb}% <br> |
||
| + | \usepackage{hyperref}% <br> |
||
| + | \usepackage{rotating}% <br> |
||
| + | \usepackage[utf8x]{inputenc}% <br> |
||
| + | \usepackage[english,russian]{babel}% <br> |
||
| + | \usepackage{color}% <br> |
||
| + | \definecolor{red}{rgb}{1,0.1,0.1}% <br> |
||
| + | \definecolor{black}{rgb}{0,0,0}% <br> |
||
| + | \definecolor{white}{rgb}{1,1,1}% <br> |
||
| + | \definecolor{yellow}{rgb}{1,.93,0}% <br> |
||
| + | \definecolor{bluedark}{rgb}{0,0,.87}% <br> |
||
| + | \paperwidth 528pt% <br> |
||
| + | \paperheight 488pt% <br> |
||
| + | \topmargin -102pt% <br> |
||
| + | \oddsidemargin -78pt% <br> |
||
| + | \textwidth 610pt% <br> |
||
| + | \textheight 570pt% <br> |
||
| + | % <br> |
||
| + | \newcommand \sx {\scalebox}% <br> |
||
| + | \newcommand \ing {\includegraphics}% <br> |
||
| + | \newcommand \tet {\mathrm{tet}}% <br> |
||
| + | \newcommand \pen {\mathrm{pen}}% <br> |
||
| + | \newcommand \bC {\mathbb C}% <br> |
||
| + | \newcommand \fac {\mathrm {Factorial}}% <br> |
||
| + | \newcommand \rme {\mathrm e}% <br> |
||
| + | \newcommand \rmi {\mathrm i}% <br> |
||
| + | \newcommand \ds {\displaystyle}% <br> |
||
| + | \newcommand \rot {\begin{rotate}}% <br> |
||
| + | \newcommand \ero {\end{rotate}}% <br> |
||
| + | % <br> |
||
| + | \begin{document}% <br> |
||
| + | \parindent 0pt% <br> |
||
| + | \sx{4}% <br> |
||
| + | {\normalsize% <br> |
||
| + | \begin{picture}(155,122)% <br> |
||
| + | \put(0,0){\ing{tet10bx}}% <br> |
||
| + | %\put(-2,125){\sx{.7}{$y\!=\!{\rm tet}_{b}(x)$ ~as solution of~ $F(z\!+\!1)=\exp_b(F(z))$ ~,~ $F(0)\!=\!1$}}% <br> |
||
| + | %\put( 0,125){\sx{.55}{$y\!=\!F(x)$ ~as solution of~ $F(z\!+\!1)\!=\!\exp_b(F(z))$ ,~ $F(0)\!=\!1$}}% <br> |
||
| + | \put( 17,120){\sx{.6}{$y$}}% <br> |
||
| + | \put( 17,100){\sx{.6}{$8$}}% <br> |
||
| + | \put( 17,80){\sx{.6}{$6$}}% <br> |
||
| + | \put( 17,60){\sx{.6}{$4$}}% <br> |
||
| + | \put( 18,48){\sx{.6}{e}}% <br> |
||
| + | \put( 17,40){\sx{.6}{$2$}}% <br> |
||
| + | \put( 17,20){\sx{.6}{$0$}}% <br> |
||
| + | \put( 20.4,16){\sx{.6}{$0$}}% <br> |
||
| + | \put( 40.4,16){\sx{.6}{$2$}}% <br> |
||
| + | \put( 60.4,16){\sx{.6}{$4$}}% <br> |
||
| + | \put( 80.4,16){\sx{.6}{$6$}}% <br> |
||
| + | \put(100.4,16){\sx{.6}{$8$}}% <br> |
||
| + | \put(119,16){\sx{.6}{$10$}}% <br> |
||
| + | \put(128.6,16.2){\sx{.6}{$x$}}% <br> |
||
| + | %\put(2,90){\sx{.9}{$y\!=\!e\!\big(F_{1}(x\!+\!\rmi o)\big)$}}% <br> |
||
| + | %\put(183,105){\sx{1.}{$y\!=\!F_{3}(x)$}}% <br> |
||
| + | %\put(193,52){\sx{1.}{$y\!=\!\rme$}}% <br> |
||
| + | \put(26.6,86){\sx{.5}{\rot{90} $b\!\rightarrow\!\infty$ \ero } }% <br> |
||
| + | \put(31,106){\sx{.5}{\rot{88} $b\!=\!10$ \ero } }% <br> |
||
| + | %\put(39.2,106){\sx{.5}{\rot{86} $b\!=\! 3$ \ero } }% <br> |
||
| + | \put(42,87){\sx{.5}{\rot{87} $b\!=\! \rme$ \ero } }% <br> |
||
| + | \put(48.4,106){\sx{.5}{\rot{86} $b\!=\!2$ \ero } }% <br> |
||
| + | \put(53.3,106){\sx{.45}{\rot{85} $b\!=\!1.9$ \ero } }% <br> |
||
| + | \put(60.3,106){\sx{.45}{\rot{85} $b\!=\!1.8$ \ero } }% <br> |
||
| + | \put(68.4,106){\sx{.45}{\rot{84} $b\!=\!1.7$ \ero } }% <br> |
||
| + | \put(83,106){\sx{.45}{\rot{83} $b\!=\!1.6$ \ero } }% <br> |
||
| + | \put(128,106){\sx{.47}{\rot{80} $b\!=\!1.5$ \ero } }% <br> |
||
| + | %\put(55,88){\sx{1.3}{$y\!=\!\tet_b(x)$ } }% <br> |
||
| + | %\put(124,106){\sx{.6}{$b\!=\!1.5$}}% <br> |
||
| + | \put(109,46){\sx{.4}{\rot{2}$b\!=\!\exp(1/\rme)$\ero}}% <br> |
||
| + | \put(120,41.8){\sx{.34}{$b\!=\!\sqrt{2}$}}% <br> |
||
| + | \put(120,38){\sx{.36}{$b\!=\!1.4$}}% <br> |
||
| + | \put(120,33.6){\sx{.36}{$b\!=\!1.2$}}% <br> |
||
| + | %\put(115,29.6){\sx{.36}{$b\!=\!1.1$}}% <br> |
||
| + | \put(123,29){\sx{.36}{$b\!\rightarrow\!1$}}% <br> |
||
| + | \end{picture}}% <br> |
||
| + | \end{document} |
||
| + | </nowiki> |
||
| + | |||
| + | [[Category:tetration]] |
||
| + | [[Category:Real–real plots]] |
||
| + | [[Category:Mathematical functions]] |
||
Revision as of 09:38, 21 June 2013
Plot of Tetration: $y=\mathrm{tet}_b(x)$ versus $x$ for
- $b \rightarrow 1$,
- $b = 1.1$,
- $b = 1.2$,
- $b = 1.3$,
- $b = 1.4$,
- $b = \sqrt{2}\approx 1.41,$
- $b = \exp(1/ \mathrm e) \approx 1.44,$
- $b = 1.5$,
- $b = 1.6$,
- $b = 1.7$,
- $b = 1.8$,
- $b = 1.9$,
- $b = 2$,
- $b = \mathrm e \approx 2.71$,
- $b = 10$,
- $b \rightarrow \infty$.
Improved version of the previous pit
Copyleft 2010 by Dmitrii Kouznetsov: Please attribute the source at the reuse: it helps to trace errors if any
C++ generator of curves
// Files GLxw2048.inc, f2048ten.inc, f4ten.cin, fit1.cin should be loaded to the working directory in order to compile the C++ code below:
#include <math.h> #include <stdio.h> #include <stdlib.h> #define DB double #define DO(x,y) for(x=0;x<y;x++) using namespace std; #include <complex> typedef complex<double> z_type; #define Re(x) x.real() #define Im(x) x.imag() #define I z_type(0.,1.)
//b=10 #include "f4ten.cin"
#include "fit1.cin"
void ado(FILE *O, int X, int Y)
{ fprintf(O,"%c!PS-Adobe-2.0 EPSF-2.0\n",'%');
fprintf(O,"%c%cBoundingBox: 0 0 %d %d\n",'%','%',X,Y);
fprintf(O,"/M {moveto} bind def\n");
fprintf(O,"/L {lineto} bind def\n");
fprintf(O,"/S {stroke} bind def\n");
fprintf(O,"/s {show newpath} bind def\n");
fprintf(O,"/C {closepath} bind def\n");
fprintf(O,"/F {fill} bind def\n");
fprintf(O,"/o {.1 0 360 arc C S} bind def\n");
fprintf(O,"/times-Roman findfont 20 scalefont setfont\n");
fprintf(O,"/W {setlinewidth} bind def\n");
fprintf(O,"/RGB {setrgbcolor} bind def\n");}
//#include "ado.cin"
#define M(x,y) fprintf(o,"%6.4f %6.4f M\n",0.+x,0.+y); #define L(x,y) fprintf(o,"%6.4f %6.4f L\n",0.+x,0.+y); #define o(x,y) fprintf(o,"%6.4f %6.4f o\n",0.+x,0.+y);
main(){ int j,k,m,n; DB p,q,t1,t3,u,v,w,x,y; z_type z,c,d;
FILE *o;o=fopen("tet10bx.eps","w");ado(o,134,124);
fprintf(o,"22 22 translate\n 10 10 scale\n");
fprintf(o,"2 setlinecap\n");
for(m=-2;m<12;m++){if(m!=0){M(m,-2)L(m,10)}}
for(n= -2;n<11;n++){if(n!=0){M(-2,n)L(11,n)}} fprintf(o,".006 W 0 0 0 RGB S\n");
M(-2,0)L(11.1,0) M(0, -2)L(0,10.1) fprintf(o,".03 W 0 0 0 RGB S\n");
M(0,M_E)L(11.,M_E) fprintf(o,".006 W 0 0 0 RGB S\n");
fprintf(o,"1 setlinejoin 1 setlinecap\n");
//DO(m,400){x=-1.99+.008*m;y=Re(FIT1(log(10.),x)); if(y>10.3) break; if(m==0)M(x,y)else L(x,y)} fprintf(o,".03 W .5 0 .5 RGB S\n");
DO(m,400){x=-1.80+.02*m; y=Re(FIT1(log(2.),x)); if(y>10.3) break; if(m==0)M(x,y)else L(x,y)} fprintf(o,".03 W .5 0 .5 RGB S\n");
DO(m,400){x=-1.78+.02*m; y=Re(FIT1(log(1.9),x)); if(y>10.33) break; if(m==0)M(x,y)else L(x,y)} fprintf(o,".02 W 0 .5 0 RGB S\n");
DO(m,400){x=-1.77+.02*m; y=Re(FIT1(log(1.8),x)); if(y>10.33) break; if(m==0)M(x,y)else L(x,y)} fprintf(o,".02 W 0 .5 0 RGB S\n");
DO(m,400){x=-1.74+.02*m; y=Re(FIT1(log(1.7),x)); if(y>10.3) break; if(m==0)M(x,y)else L(x,y)} fprintf(o,".02 W 0 .5 0 RGB S\n");
DO(m,400){x=-1.72+.03*m; y=Re(FIT1(log(1.6),x)); if(y>10.3) break; if(m==0)M(x,y)else L(x,y)} fprintf(o,".02 W 0 .5 0 RGB S\n");
DO(m,400){x=-1.68+.04*m; y=Re(FIT1(log(1.5),x)); if(y>10.3) break; if(m==0)M(x,y)else L(x,y)} fprintf(o,".02 W 0 .5 0 RGB S\n");
DO(m,400){x=-1.64+.04*m; y=Re(FIT1(log(1.4),x)); if(x>11.1) break; if(m==0)M(x,y)else L(x,y)} fprintf(o,".02 W 0 .5 0 RGB S\n");
DO(m,400){x=-1.58+.04*m; y=Re(FIT1(log(1.3),x)); if(x>11.1) break; if(m==0)M(x,y)else L(x,y)} fprintf(o,".02 W 0 .5 0 RGB S\n");
DO(m,400){x=-1.52+.04*m; y=Re(FIT1(log(1.2),x)); if(x>11.1) break; if(m==0)M(x,y)else L(x,y)} fprintf(o,".02 W 0 .5 0 RGB S\n");
DO(m,400){x=-1.42+.04*m; y=Re(FIT1(log(1.1),x)); if(x>11.1) break; if(m==0)M(x,y)else L(x,y)} fprintf(o,".02 W 0 .5 0 RGB S\n");
//
DO(m,400){x=-1.65+.04*m; y=Re(FIT1(1./M_E,x)); if(x>11.1) break; if(m==0)M(x,y)else L(x,y)} fprintf(o,".03 W 0 0 .7 RGB S\n");
DO(m,400){x=-1.64+.04*m; y=Re(FIT1(log(sqrt(2.)),x)); if(x>11.1) break; if(m==0)M(x,y)else L(x,y)} fprintf(o,".03 W .8 0 0 RGB S\n");
DO(m,400){x=-1.873+.01*m; y=Re(FIT1(1.,x)); if(y>11) break; if(m==0)M(x,y)else L(x,y)} fprintf(o,".02 W 0 0 0 RGB S\n");
//
DO(m,401){x=-1.987+.01*m;y=Re(F4TEN(x));if(m==0)M(x,y)else L(x,y)}fprintf(o,".02 W .5 0 .5 RGB S\n");
//DO(m,39){x=-1.89+.098*m; y=Re(FSEXP(x));if(m==0)M(x,y)else L(x,y)} fprintf(o,".01 W 0 0 0 RGB S\n");
//DO(m,48){x=-1.82+.0973*m; y=Re(F2(x)); if(m==0)M(x,y)else L(x,y)} fprintf(o,".01 W 0 0 0 RGB S\n");
//DO(m,126){x=-1.72+.1*m; y=Re(F15(x)); if(m==0)M(x,y)else L(x,y)} fprintf(o,".01 W 0 0 0 RGB S\n");
//DO(m,130){x=-1.65+.1*m; y=Re(E1ETF(x)); if(m==0)M(x,y)else L(x,y)} fprintf(o,".01 W 0 0 0 RGB S\n");
//DO(m,130){x=-1.64+.1*m; y=Re(f21E(x)); if(m==0)M(x,y)else L(x,y)} fprintf(o,".01 W 0 0 0 RGB S\n");
M(-1.998,-2)L(-1.992,-.01)L(-1,0)L(-.01,.01)L(0,1)L(.012,10.1) fprintf(o,".02 W .4 0 .8 RGB S\n");
M(-1.01,-2)L(-1,0)L(-.99,.99)L(0,1)L(10.97,1.01) fprintf(o,".02 W .2 .4 0 RGB S\n");
fprintf(o,"showpage\n%cTrailer",'%'); fclose(o);
system("epstopdf tet10bx.eps");
system( "open tet10bx.pdf"); //mac
// system( "xpdf tet10bx.pdf"); // linux
getchar(); system("killall Preview");// mac
}
Latex generator of curves
% File tet10bx.pdf sould be generated with code above in order to compile the Latex document below %
%
\documentclass[12pt]{article} % <br>
\usepackage{geometry} % See geometry.pdf % <br>
\geometry{letterpaper} % ... or a4paper or a5paper or ... ??% <br>
\usepackage{graphicx}% <br>
\usepackage{amssymb}% <br>
\usepackage{hyperref}% <br>
\usepackage{rotating}% <br>
\usepackage[utf8x]{inputenc}% <br>
\usepackage[english,russian]{babel}% <br>
\usepackage{color}% <br>
\definecolor{red}{rgb}{1,0.1,0.1}% <br>
\definecolor{black}{rgb}{0,0,0}% <br>
\definecolor{white}{rgb}{1,1,1}% <br>
\definecolor{yellow}{rgb}{1,.93,0}% <br>
\definecolor{bluedark}{rgb}{0,0,.87}% <br>
\paperwidth 528pt% <br>
\paperheight 488pt% <br>
\topmargin -102pt% <br>
\oddsidemargin -78pt% <br>
\textwidth 610pt% <br>
\textheight 570pt% <br>
% <br>
\newcommand \sx {\scalebox}% <br>
\newcommand \ing {\includegraphics}% <br>
\newcommand \tet {\mathrm{tet}}% <br>
\newcommand \pen {\mathrm{pen}}% <br>
\newcommand \bC {\mathbb C}% <br>
\newcommand \fac {\mathrm {Factorial}}% <br>
\newcommand \rme {\mathrm e}% <br>
\newcommand \rmi {\mathrm i}% <br>
\newcommand \ds {\displaystyle}% <br>
\newcommand \rot {\begin{rotate}}% <br>
\newcommand \ero {\end{rotate}}% <br>
% <br>
\begin{document}% <br>
\parindent 0pt% <br>
\sx{4}% <br>
{\normalsize% <br>
\begin{picture}(155,122)% <br>
\put(0,0){\ing{tet10bx}}% <br>
%\put(-2,125){\sx{.7}{$y\!=\!{\rm tet}_{b}(x)$ ~as solution of~ $F(z\!+\!1)=\exp_b(F(z))$ ~,~ $F(0)\!=\!1$}}% <br>
%\put( 0,125){\sx{.55}{$y\!=\!F(x)$ ~as solution of~ $F(z\!+\!1)\!=\!\exp_b(F(z))$ ,~ $F(0)\!=\!1$}}% <br>
\put( 17,120){\sx{.6}{$y$}}% <br>
\put( 17,100){\sx{.6}{$8$}}% <br>
\put( 17,80){\sx{.6}{$6$}}% <br>
\put( 17,60){\sx{.6}{$4$}}% <br>
\put( 18,48){\sx{.6}{e}}% <br>
\put( 17,40){\sx{.6}{$2$}}% <br>
\put( 17,20){\sx{.6}{$0$}}% <br>
\put( 20.4,16){\sx{.6}{$0$}}% <br>
\put( 40.4,16){\sx{.6}{$2$}}% <br>
\put( 60.4,16){\sx{.6}{$4$}}% <br>
\put( 80.4,16){\sx{.6}{$6$}}% <br>
\put(100.4,16){\sx{.6}{$8$}}% <br>
\put(119,16){\sx{.6}{$10$}}% <br>
\put(128.6,16.2){\sx{.6}{$x$}}% <br>
%\put(2,90){\sx{.9}{$y\!=\!e\!\big(F_{1}(x\!+\!\rmi o)\big)$}}% <br>
%\put(183,105){\sx{1.}{$y\!=\!F_{3}(x)$}}% <br>
%\put(193,52){\sx{1.}{$y\!=\!\rme$}}% <br>
\put(26.6,86){\sx{.5}{\rot{90} $b\!\rightarrow\!\infty$ \ero } }% <br>
\put(31,106){\sx{.5}{\rot{88} $b\!=\!10$ \ero } }% <br>
%\put(39.2,106){\sx{.5}{\rot{86} $b\!=\! 3$ \ero } }% <br>
\put(42,87){\sx{.5}{\rot{87} $b\!=\! \rme$ \ero } }% <br>
\put(48.4,106){\sx{.5}{\rot{86} $b\!=\!2$ \ero } }% <br>
\put(53.3,106){\sx{.45}{\rot{85} $b\!=\!1.9$ \ero } }% <br>
\put(60.3,106){\sx{.45}{\rot{85} $b\!=\!1.8$ \ero } }% <br>
\put(68.4,106){\sx{.45}{\rot{84} $b\!=\!1.7$ \ero } }% <br>
\put(83,106){\sx{.45}{\rot{83} $b\!=\!1.6$ \ero } }% <br>
\put(128,106){\sx{.47}{\rot{80} $b\!=\!1.5$ \ero } }% <br>
%\put(55,88){\sx{1.3}{$y\!=\!\tet_b(x)$ } }% <br>
%\put(124,106){\sx{.6}{$b\!=\!1.5$}}% <br>
\put(109,46){\sx{.4}{\rot{2}$b\!=\!\exp(1/\rme)$\ero}}% <br>
\put(120,41.8){\sx{.34}{$b\!=\!\sqrt{2}$}}% <br>
\put(120,38){\sx{.36}{$b\!=\!1.4$}}% <br>
\put(120,33.6){\sx{.36}{$b\!=\!1.2$}}% <br>
%\put(115,29.6){\sx{.36}{$b\!=\!1.1$}}% <br>
\put(123,29){\sx{.36}{$b\!\rightarrow\!1$}}% <br>
\end{picture}}% <br>
\end{document}
File history
Click on a date/time to view the file as it appeared at that time.
| Date/Time | Thumbnail | Dimensions | User | Comment | |
|---|---|---|---|---|---|
| current | 17:50, 20 June 2013 | 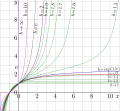 | 2,192 × 2,026 (436 KB) | Maintenance script (talk | contribs) | Importing image file |
You cannot overwrite this file.
File usage
The following 7 pages use this file: