Difference between revisions of "Precision"
| (10 intermediate revisions by the same user not shown) | |||
| Line 4: | Line 4: | ||
==Definition== |
==Definition== |
||
| + | <div style="margin:-18px -14px 0px -200px; background-color:#fff"> |
||
| − | Let \(M\) is range of allowed variation of some quality and<br> |
||
| + | <div style="margin:0px 0px 0px 30px; line-height:1.2em"><br> |
||
| + | Let \(M\) is length of the interval of values allowed for some quality and<br> |
||
let \( s \) be maximal deviation of the evaluated quantity from some "true", "exact" value.<br> |
let \( s \) be maximal deviation of the evaluated quantity from some "true", "exact" value.<br> |
||
| − | Then, [[precision]] |
+ | Then, the [[precision]] |
\(\displaystyle |
\(\displaystyle |
||
| Line 19: | Line 21: | ||
==Examples== |
==Examples== |
||
| − | <div style="margin:-18px -14px 0px -200px; background-color:#fff"> |
||
| − | <div style="margin:0px 0px 0px 30px; line-height:1.2em"><br> |
||
===Temperature of water=== |
===Temperature of water=== |
||
| Line 47: | Line 47: | ||
to make the wise decision. |
to make the wise decision. |
||
| − | ===Exercise=== |
+ | ===Exercise 1=== |
Elsa has a two-story cottage in the countryside. She wants to update the stair. She calls the construction company. The agent asks to measure the altitude of the second floor. |
Elsa has a two-story cottage in the countryside. She wants to update the stair. She calls the construction company. The agent asks to measure the altitude of the second floor. |
||
| Line 56: | Line 56: | ||
GPS measures height with an error of half a meter. |
GPS measures height with an error of half a meter. |
||
| − | In principle, the level of the floor can vary, roughly, from -432 meters to |
+ | In principle, the level of the floor can vary, roughly, from -432 meters to 8000 meters. |
| − | Did Elsa measure the height of the second floor with precision of five significant figures? |
+ | Did Elsa measure the height of the second floor with precision of five significant decimal figures? |
| − | + | Is this accuracy sufficient to choose the right stair for her cottage? |
|
Comment: Elsa is very intelligent girl. She knows, that in the practical life, usually, only the relative quantities have sense. (Since A.Einstein, it is well known, that everything is relative.) So, Elsa did not even try to calculate the distance from her second floor to the center of the Earth. She measures and reports the relative altitude, above the sea level. |
Comment: Elsa is very intelligent girl. She knows, that in the practical life, usually, only the relative quantities have sense. (Since A.Einstein, it is well known, that everything is relative.) So, Elsa did not even try to calculate the distance from her second floor to the center of the Earth. She measures and reports the relative altitude, above the sea level. |
||
| + | |||
| + | ===Exercise 2=== |
||
| + | What is precision of evaluation of result of arithmetic operation with the [[Alternative Math]] |
||
| + | <ref> |
||
| + | https://www.youtube.com/watch?v=Zh3Yz3PiXZw |
||
| + | Alternative Math. |
||
| + | Sep 19, 2017 |
||
| + | </ref> ( it assumes, that 2+2 gives 22 ) ? |
||
| + | |||
| + | ==Agreement== |
||
| + | |||
| + | At the numerical calculus, the floating point arithmetic is popular. |
||
| + | In particular, the most of calculus descried in book [[Superfunctions]] |
||
| + | <ref name="m"> |
||
| + | https://www.morebooks.de/store/gb/book/superfunctions/isbn/978-620-2-67286-3 |
||
| + | Dmitrii Kouznetsov. [[Superfunctions]]. [[Lambert Academic Publishing]], 2020.07.28. |
||
| + | </ref><ref name="t"> |
||
| + | https://mizugadro.mydns.jp/BOOK/466.pdf |
||
| + | Dmitrii Kouznetsov. [[Superfunctions]]. [[Lambert Academic Publishing]], 2020. |
||
| + | </ref> |
||
| + | is performed using the complex double arithmetics. In such a calculus, the internal rounding error of evaluation of each quantity is of order of \( 10^{-16} \) of the value. |
||
| + | In this case, the length of the interval of variation of the quantity (while the same precision holds) is of order the quantity. |
||
| + | |||
| + | Usually, several operations are performed to get value; so, the actual error happen to be an order of magnitude larger. In order to estimate the stability of an algorithm, it has sense to compare, how close the precision achieved approaches the best possible (for the given type of a variable). for such a qualification of an algorithm, the agreement is defined: |
||
| + | |||
| + | \( \displaystyle |
||
| + | A=-\log_{10} \left( \frac |
||
| + | {|x-y|} |
||
| + | {|x|+|y|} |
||
| + | \right) \) |
||
| + | |||
| + | where |
||
| + | \( x \) and |
||
| + | \( y \) |
||
| + | are estimates of the same quantity, obtained in different ways. |
||
| + | |||
| + | Such Agreement appears as an estimate of the [[precision]] achieved in the numerical calculus. In book [[Superfunctions]], the most of quantities are evaluated with precision \(P=14\) that is close to the maximal achievable for the complex double variables. |
||
| + | |||
| + | <div style="float:right; margin:-4px 0px 0px 0px"> |
||
| + | [[File:Sqrt2sufuplot.png|400px]]<small><center>Four superexponentials to base \(\sqrt{2}\) |
||
| + | <ref>https://www.morebooks.de/store/ru/book/Суперфункции/isbn/978-3-659-56202-0 <br> |
||
| + | http://www.ils.uec.ac.jp/~dima/BOOK/202.pdf<br> |
||
| + | http://mizugadro.mydns.jp/BOOK/202.pdf<br> |
||
| + | Д.Кузнецов. Суперфункции. (In Russian) Lambert Academic Publishing, 2014. Fig.16.10. |
||
| + | </ref></center></small></div> |
||
| + | The only one example has been detected, when these 14 decimals happen to be not sufficient for the numerical analysis of mathematical functions. |
||
| + | It refers to the two superexponentials to base \( \sqrt{2} \); they are denoted as |
||
| + | \( F_{2,3} \) |
||
| + | and |
||
| + | \( F_{4,3}\). |
||
| + | |||
| + | Each of them is real-holomorphic and satisfies equation |
||
| + | |||
| + | \( \exp_b(F(z))=F(z\!+\!1) \) |
||
| + | |||
| + | for \(b = \sqrt{2} \) |
||
| + | |||
| + | and the additional requirement \( F(0)=3 \) . |
||
| + | |||
| + | Superexponential \( F_{2,3}\) is constructed with [[Regular iteration]] of \( \exp_b \) |
||
| + | at the [[fixed point]] 2 , and |
||
| + | Superexponential \( F_{4,3}\) is constructed with [[Regular iteration]] of \( \exp_b \) |
||
| + | at the [[fixed point]] 4. Only in the strip along the real axis, these functions look similar. |
||
| + | |||
| + | The C++ routines for the evaluation are loaded as |
||
| + | [[Sqrt2f21e.cin]] and [[Sqrt2f43e.cin]] . |
||
| + | |||
| + | Along the real axis, these routines happen to return the almost same value (with some rounding errors). |
||
| + | The coincidence was unexpected and looked as a marvel; it could be considered as a hint to some internal contradiction of arithmetics (see «[[Mizugadro number]]»). |
||
| + | <br> |
||
| + | At the analysis, the crash of the Arithmetic is not confirmed. |
||
| + | The deviation is clearly seen if the calculus is performed with a hundred decimals and/or if the comparison is performed at significant imaginary part of the argument: the two functions have different periodicity and cannot remain close in wide range at the complex plane. These functions are described in the book |
||
| + | <ref name="m"/><ref name="t"/>, and also in article <ref> |
||
| + | https://www.ams.org/journals/mcom/2010-79-271/S0025-5718-10-02342-2/home.html |
||
| + | Dmitrii Kouznetsov and Henryk Trappmann. |
||
| + | Portrait of the four regular super-exponentials to base sqrt(2). |
||
| + | Journal: Math. Comp. 79 (2010), 1727-1756 |
||
| + | MSC (2000): Primary 30A99; Secondary 33F99 |
||
| + | DOI: https://doi.org/10.1090/S0025-5718-10-02342-2 |
||
| + | Published electronically: February 12, 2010 |
||
| + | MathSciNet review: 2630010 |
||
| + | Full-text PDF Free Access |
||
| + | </ref>. |
||
| + | Along the real axis, functions |
||
| + | \(F_{2,3} \) and |
||
| + | \(F_{4,3} \) coincide with 24 decimal figures; |
||
| + | the deviation |
||
| + | |||
| + | \( d_{42}(x)=F_{4,3}(x)-F_{2,3}(x) \) |
||
| + | |||
| + | scaled with factor \(10^{24} \) is shown in the Figure with violet sinusoidal bell. |
||
| + | Without such a scaling, it would not be seen. |
||
| + | |||
| + | The only one example is detected, when the complex double [[precision]] happen to be not sufficient to distinguish the functions. |
||
| + | In other cases, the Agreement defined above seems to be good criterion, analogy of the [[Precision]]. |
||
==Rounding== |
==Rounding== |
||
| Line 82: | Line 177: | ||
in the same way as some coauthors do not know the difference between [[Probability]] and [[math expectation]];<br> |
in the same way as some coauthors do not know the difference between [[Probability]] and [[math expectation]];<br> |
||
or cannot distinguish an integral from a logarithm;<br> |
or cannot distinguish an integral from a logarithm;<br> |
||
| − | or even |
+ | or even insist, that \(\pi\) is an approximate number. |
| + | |||
| + | One of goals of [[TORI]] is identification and qualification of such phenomena. |
||
==References== |
==References== |
||
| + | </div> |
||
| + | <small> |
||
| + | <div style="margin:0px 0px 0px 10px; line-height:1em"> |
||
<references/> |
<references/> |
||
| + | </div> |
||
| + | <div style="margin:0px 0px 0px 30px; line-height:1em"> |
||
| + | https://en.wikipedia.org/wiki/Significant_figures |
||
| + | Significant figures (also known as the significant digits, precision or resolution) of a number in positional notation are digits in the number that are reliable and necessary to indicate the quantity of something. |
||
| + | |||
| + | 2022.06.10. |
||
| + | https://tech.wikireading.ru/6667 |
||
| + | Перля Зигмунд Наумович. Точность в 0,001 миллиметра. |
||
| + | |||
| + | 2022.06.10. |
||
| + | https://satu.kz/p80573218-portativnyj-laboratornye-vesy.html |
||
| + | Электронные весы с миллиграммовой точностью. |
||
| + | |||
| + | </div> |
||
| + | </small> |
||
| + | <div style="margin:0px 0px 0px 30px; line-height:1.2em"> |
||
==Keywords== |
==Keywords== |
||
| + | [[Confusion]], |
||
| + | [[Female logic]], |
||
[[Measurement]], |
[[Measurement]], |
||
| − | [[Precision]] |
+ | [[Precision]], |
| + | [[Science]] |
||
[[Точность]] |
[[Точность]] |
||
| Line 96: | Line 215: | ||
[[Category:Measurement]] |
[[Category:Measurement]] |
||
[[Category:Precision]] |
[[Category:Precision]] |
||
| + | [[Category:Science]] |
||
Latest revision as of 18:09, 11 June 2022
Precision (Number of significant decimals, Точность) is specification of an approximate evaluation of some quantity (experimental or numerical), characterizing its accuracy, precision.
Precision of some quantity indicates, how well it is evaluated.
Definition
Let \(M\) is length of the interval of values allowed for some quality and
let \( s \) be maximal deviation of the evaluated quantity from some "true", "exact" value.
Then, the precision
\(\displaystyle N = \log_{10} \left(\frac M s \right)\)
The precision is usually rounded down to integer. Then, it happens to be
\(\displaystyle P=\mathrm{round\_down} (N) \)
Examples
Temperature of water
In usual conditions (at the atmospheric pressure), temperature of water varies, roughly, from 273 Kelvin to 373 Kelvin.
Let one says, that water temperature is 299 Kelvins. If well measured, this may refer to the maximal deviation 0.5 , that is half of the last digit. Then, the precision
\( N = \log_{10}(100/0.5) = \log_{10}(200) \approx 2.301029995664 \approx 2 \)
The correct estimate of the precision at the evaluation of temperature of liquid is very important for the correct treatment of specifications of liquids, for example, the statement «The tea is absolutely cold!»
The Researcher is supposed to estimate the temperature and quality the precision of this estimate. The advanced guide how to treat specification «absolutely cold» is suggested in article «Female logic».
Scratched jeans
One researcher, being in a foreign country and having few cash, looks for some used clothes. He sees the jeans that looks a little bit scratched. The researcher reads the price price tag, recalculates the price to dollars, and tries to understand, why the used jeans cost two hundred dollars, higher than a new jeans. The relative error of the price (due to uncertainty at the money exchange) could be of order of 10 percent, while the researcher knows, that means usually cost from 8 to 20 dollars. The formula above would indicate, that the precision
\( N = \log_{10}(10\% * 200/ 12) \approx 0 \)
The researchers realizes, that the price is estimated with 0 significant decimals, and tries to express his opinion with the aboriginal dialect: why the used jeans cost higher than a new clothes. (However, the store owner explains that this is a special fashion style, extremely popular among bon vivants.)
In such a way, estimate of the Number of significant decimals helps the researcher to make the wise decision.
Exercise 1
Elsa has a two-story cottage in the countryside. She wants to update the stair. She calls the construction company. The agent asks to measure the altitude of the second floor.
Elsa puts the GPS on the floor and answers: «2834 meters above sea level».
GPS measures height with an error of half a meter.
In principle, the level of the floor can vary, roughly, from -432 meters to 8000 meters.
Did Elsa measure the height of the second floor with precision of five significant decimal figures?
Is this accuracy sufficient to choose the right stair for her cottage?
Comment: Elsa is very intelligent girl. She knows, that in the practical life, usually, only the relative quantities have sense. (Since A.Einstein, it is well known, that everything is relative.) So, Elsa did not even try to calculate the distance from her second floor to the center of the Earth. She measures and reports the relative altitude, above the sea level.
Exercise 2
What is precision of evaluation of result of arithmetic operation with the Alternative Math [1] ( it assumes, that 2+2 gives 22 ) ?
Agreement
At the numerical calculus, the floating point arithmetic is popular. In particular, the most of calculus descried in book Superfunctions [2][3] is performed using the complex double arithmetics. In such a calculus, the internal rounding error of evaluation of each quantity is of order of \( 10^{-16} \) of the value. In this case, the length of the interval of variation of the quantity (while the same precision holds) is of order the quantity.
Usually, several operations are performed to get value; so, the actual error happen to be an order of magnitude larger. In order to estimate the stability of an algorithm, it has sense to compare, how close the precision achieved approaches the best possible (for the given type of a variable). for such a qualification of an algorithm, the agreement is defined:
\( \displaystyle A=-\log_{10} \left( \frac {|x-y|} {|x|+|y|} \right) \)
where \( x \) and \( y \) are estimates of the same quantity, obtained in different ways.
Such Agreement appears as an estimate of the precision achieved in the numerical calculus. In book Superfunctions, the most of quantities are evaluated with precision \(P=14\) that is close to the maximal achievable for the complex double variables.
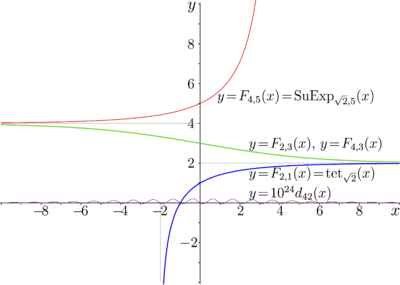
The only one example has been detected, when these 14 decimals happen to be not sufficient for the numerical analysis of mathematical functions. It refers to the two superexponentials to base \( \sqrt{2} \); they are denoted as \( F_{2,3} \) and \( F_{4,3}\).
Each of them is real-holomorphic and satisfies equation
\( \exp_b(F(z))=F(z\!+\!1) \)
for \(b = \sqrt{2} \)
and the additional requirement \( F(0)=3 \) .
Superexponential \( F_{2,3}\) is constructed with Regular iteration of \( \exp_b \) at the fixed point 2 , and Superexponential \( F_{4,3}\) is constructed with Regular iteration of \( \exp_b \) at the fixed point 4. Only in the strip along the real axis, these functions look similar.
The C++ routines for the evaluation are loaded as Sqrt2f21e.cin and Sqrt2f43e.cin .
Along the real axis, these routines happen to return the almost same value (with some rounding errors).
The coincidence was unexpected and looked as a marvel; it could be considered as a hint to some internal contradiction of arithmetics (see «Mizugadro number»).
At the analysis, the crash of the Arithmetic is not confirmed.
The deviation is clearly seen if the calculus is performed with a hundred decimals and/or if the comparison is performed at significant imaginary part of the argument: the two functions have different periodicity and cannot remain close in wide range at the complex plane. These functions are described in the book
[2][3], and also in article [5].
Along the real axis, functions
\(F_{2,3} \) and
\(F_{4,3} \) coincide with 24 decimal figures;
the deviation
\( d_{42}(x)=F_{4,3}(x)-F_{2,3}(x) \)
scaled with factor \(10^{24} \) is shown in the Figure with violet sinusoidal bell. Without such a scaling, it would not be seen.
The only one example is detected, when the complex double precision happen to be not sufficient to distinguish the functions. In other cases, the Agreement defined above seems to be good criterion, analogy of the Precision.
Rounding
Precision may refer to the problem of rounding. The solution is suggested to avoid these problems:
One friend of mine found:
Let all constants be round!
Let both, \( \pi \) and \(\mathrm e \)
Be equal to three,
And kilogram be 2 lb
Confusions
Some authors use confusing notation.
Especially this refers to terms related to Precision, number of significant decimals, uncertainty, Error.
The use of the confusing notations indicates, that the author does not understand
the difference between uncertainty, dispersion, error and mistake,
in the same way as some coauthors do not know the difference between Probability and math expectation;
or cannot distinguish an integral from a logarithm;
or even insist, that \(\pi\) is an approximate number.
One of goals of TORI is identification and qualification of such phenomena.
References
- ↑ https://www.youtube.com/watch?v=Zh3Yz3PiXZw Alternative Math. Sep 19, 2017
- ↑ Jump up to: 2.0 2.1 https://www.morebooks.de/store/gb/book/superfunctions/isbn/978-620-2-67286-3 Dmitrii Kouznetsov. Superfunctions. Lambert Academic Publishing, 2020.07.28.
- ↑ Jump up to: 3.0 3.1 https://mizugadro.mydns.jp/BOOK/466.pdf Dmitrii Kouznetsov. Superfunctions. Lambert Academic Publishing, 2020.
- ↑ https://www.morebooks.de/store/ru/book/Суперфункции/isbn/978-3-659-56202-0
http://www.ils.uec.ac.jp/~dima/BOOK/202.pdf
http://mizugadro.mydns.jp/BOOK/202.pdf
Д.Кузнецов. Суперфункции. (In Russian) Lambert Academic Publishing, 2014. Fig.16.10. - ↑ https://www.ams.org/journals/mcom/2010-79-271/S0025-5718-10-02342-2/home.html Dmitrii Kouznetsov and Henryk Trappmann. Portrait of the four regular super-exponentials to base sqrt(2). Journal: Math. Comp. 79 (2010), 1727-1756 MSC (2000): Primary 30A99; Secondary 33F99 DOI: https://doi.org/10.1090/S0025-5718-10-02342-2 Published electronically: February 12, 2010 MathSciNet review: 2630010 Full-text PDF Free Access
https://en.wikipedia.org/wiki/Significant_figures Significant figures (also known as the significant digits, precision or resolution) of a number in positional notation are digits in the number that are reliable and necessary to indicate the quantity of something.
2022.06.10. https://tech.wikireading.ru/6667 Перля Зигмунд Наумович. Точность в 0,001 миллиметра.
2022.06.10. https://satu.kz/p80573218-portativnyj-laboratornye-vesy.html Электронные весы с миллиграммовой точностью.