Difference between revisions of "File:Tetreal10bx10d.png"

Latest revision as of 20:27, 17 August 2025

Explicit plot of Tetration: \(y=\mathrm{tet}_b(x)\) versus \(x\) for

\(b \rightarrow 1\),

\(b = 1.1\),

\(b = 1.2\),

\(b = 1.3\),

\(b = 1.4\),

\(b = \sqrt{2}\approx 1.41,\)

\(b = \exp(1/ \mathrm e) \approx 1.44,\)

\(b = 1.5\),

\(b = 1.6\),

\(b = 1.7\),

\(b = 1.8\),

\(b = 1.9\),

\(b = 2\),

\(b = \mathrm e \approx 2.71\),

\(b = 10\),

\(b \rightarrow \infty\).

The fit is used that provides several decimal digits: it is sufficient to make the "camera-ready copy"; the errors of the fitting are not seen even at the zooming-in.

This image is used as figure 17.2 at page 239 of book «Superfunctions» ^[1]^[2].

Copyleft 2010 by Dmitrii Kouznetsov: Please attribute the source at the reuse: it helps to trace mistakes, if any

C++ generator of curves

// Files GLxw2048.inc, f2048ten.inc, f4ten.cin, fit1.cin should be loaded in order to compile the C++ code below:

 #include <math.h>
 #include <stdio.h>
 #include <stdlib.h>
 #define DB double
 #define DO(x,y) for(x=0;x<y;x++)
 using namespace std;
 #include <complex>
 typedef complex<double> z_type;
 #define Re(x) x.real()
 #define Im(x) x.imag()
 #define I z_type(0.,1.)

 //b=10
 #include "f4ten.cin"

 #include "fit1.cin"

 void ado(FILE *O, int X, int Y)
 {      fprintf(O,"%c!PS-Adobe-2.0 EPSF-2.0\n",'%');
        fprintf(O,"%c%cBoundingBox: 0 0 %d %d\n",'%','%',X,Y);
        fprintf(O,"/M {moveto} bind def\n");
        fprintf(O,"/L {lineto} bind def\n");
        fprintf(O,"/S {stroke} bind def\n");
        fprintf(O,"/s {show newpath} bind def\n");
        fprintf(O,"/C {closepath} bind def\n");
        fprintf(O,"/F {fill} bind def\n");
        fprintf(O,"/o {.1 0 360 arc C S} bind def\n");
        fprintf(O,"/times-Roman findfont 20 scalefont setfont\n");
        fprintf(O,"/W {setlinewidth} bind def\n");
        fprintf(O,"/RGB {setrgbcolor} bind def\n");}
  //#include "ado.cin"

 #define M(x,y) fprintf(o,"%6.4f %6.4f M\n",0.+x,0.+y);
 #define L(x,y) fprintf(o,"%6.4f %6.4f L\n",0.+x,0.+y);
 #define o(x,y) fprintf(o,"%6.4f %6.4f o\n",0.+x,0.+y);

 main(){ int j,k,m,n; DB p,q,t1,t3,u,v,w,x,y; z_type z,c,d;
 FILE *o;o=fopen("tet10bx.eps","w");ado(o,134,124);
 fprintf(o,"22 22 translate\n 10 10 scale\n");
 fprintf(o,"2 setlinecap\n");
 for(m=-2;m<12;m++){if(m!=0){M(m,-2)L(m,10)}} 
 for(n= -2;n<11;n++){if(n!=0){M(-2,n)L(11,n)}}  fprintf(o,".006 W 0 0 0 RGB S\n");
 M(-2,0)L(11.1,0) M(0, -2)L(0,10.1)             fprintf(o,".03  W 0 0 0 RGB S\n");
 M(0,M_E)L(11.,M_E)                             fprintf(o,".006  W 0 0 0 RGB S\n"); 
 fprintf(o,"1 setlinejoin 1 setlinecap\n");

 //DO(m,400){x=-1.99+.008*m;y=Re(FIT1(log(10.),x)); if(y>10.3) break; if(m==0)M(x,y)else L(x,y)} fprintf(o,".03 W .5 0 .5 RGB S\n");
 DO(m,400){x=-1.80+.02*m; y=Re(FIT1(log(2.),x)); if(y>10.3) break; if(m==0)M(x,y)else L(x,y)} fprintf(o,".03 W .5 0 .5 RGB S\n");
 DO(m,400){x=-1.78+.02*m; y=Re(FIT1(log(1.9),x)); if(y>10.33) break; if(m==0)M(x,y)else L(x,y)} fprintf(o,".02 W 0 .5 0 RGB S\n");
 DO(m,400){x=-1.77+.02*m; y=Re(FIT1(log(1.8),x)); if(y>10.33) break; if(m==0)M(x,y)else L(x,y)} fprintf(o,".02 W 0 .5 0 RGB S\n");
 DO(m,400){x=-1.74+.02*m; y=Re(FIT1(log(1.7),x)); if(y>10.3) break; if(m==0)M(x,y)else L(x,y)} fprintf(o,".02 W 0 .5 0 RGB S\n");
 DO(m,400){x=-1.72+.03*m; y=Re(FIT1(log(1.6),x)); if(y>10.3) break; if(m==0)M(x,y)else L(x,y)} fprintf(o,".02 W 0 .5 0 RGB S\n");
 DO(m,400){x=-1.68+.04*m; y=Re(FIT1(log(1.5),x)); if(y>10.3) break; if(m==0)M(x,y)else L(x,y)} fprintf(o,".02 W 0 .5 0 RGB S\n");
 DO(m,400){x=-1.64+.04*m; y=Re(FIT1(log(1.4),x)); if(x>11.1) break; if(m==0)M(x,y)else L(x,y)} fprintf(o,".02 W 0 .5 0 RGB S\n");
 DO(m,400){x=-1.58+.04*m; y=Re(FIT1(log(1.3),x)); if(x>11.1) break; if(m==0)M(x,y)else L(x,y)} fprintf(o,".02 W 0 .5 0 RGB S\n");
 DO(m,400){x=-1.52+.04*m; y=Re(FIT1(log(1.2),x)); if(x>11.1) break; if(m==0)M(x,y)else L(x,y)} fprintf(o,".02 W 0 .5 0 RGB S\n");
 DO(m,400){x=-1.42+.04*m; y=Re(FIT1(log(1.1),x)); if(x>11.1) break; if(m==0)M(x,y)else L(x,y)} fprintf(o,".02 W 0 .5 0 RGB S\n");
 //
 DO(m,400){x=-1.65+.04*m; y=Re(FIT1(1./M_E,x)); if(x>11.1) break; if(m==0)M(x,y)else L(x,y)} fprintf(o,".03 W 0 0 .7 RGB S\n");
 DO(m,400){x=-1.64+.04*m; y=Re(FIT1(log(sqrt(2.)),x)); if(x>11.1) break; if(m==0)M(x,y)else L(x,y)} fprintf(o,".03 W .8 0 0 RGB S\n");
 DO(m,400){x=-1.873+.01*m; y=Re(FIT1(1.,x)); if(y>11) break; if(m==0)M(x,y)else L(x,y)} fprintf(o,".02 W 0 0 0 RGB S\n");
 //
 DO(m,401){x=-1.987+.01*m;y=Re(F4TEN(x));if(m==0)M(x,y)else L(x,y)}fprintf(o,".02 W .5 0 .5 RGB S\n");
 //DO(m,39){x=-1.89+.098*m; y=Re(FSEXP(x));if(m==0)M(x,y)else L(x,y)} fprintf(o,".01 W 0 0 0 RGB S\n");
 //DO(m,48){x=-1.82+.0973*m; y=Re(F2(x));       if(m==0)M(x,y)else L(x,y)} fprintf(o,".01 W 0 0 0 RGB S\n");
 //DO(m,126){x=-1.72+.1*m; y=Re(F15(x));        if(m==0)M(x,y)else L(x,y)} fprintf(o,".01 W 0 0 0 RGB S\n");
 //DO(m,130){x=-1.65+.1*m; y=Re(E1ETF(x));      if(m==0)M(x,y)else L(x,y)} fprintf(o,".01 W 0 0 0 RGB S\n");
 //DO(m,130){x=-1.64+.1*m; y=Re(f21E(x));       if(m==0)M(x,y)else L(x,y)} fprintf(o,".01 W 0 0 0 RGB S\n");
 M(-1.998,-2)L(-1.992,-.01)L(-1,0)L(-.01,.01)L(0,1)L(.012,10.1)  fprintf(o,".02 W .4 0 .8 RGB S\n");
 M(-1.01,-2)L(-1,0)L(-.99,.99)L(0,1)L(10.97,1.01)        fprintf(o,".02 W .2 .4 0 RGB S\n");
 fprintf(o,"showpage\n%cTrailer",'%'); fclose(o);
        system("epstopdf tet10bx.eps");
        system(    "open tet10bx.pdf"); //mac
 //     system(    "xpdf tet10bx.pdf"); // linux
 getchar(); system("killall Preview");// mac
 }

Latex generator of labels


\documentclass[12pt]{article} % <br>
\usepackage{geometry} % See geometry.pdf % <br>
\geometry{letterpaper}   % ... or a4paper or a5paper or ... ??% <br> 
\usepackage{graphicx}% <br>
\usepackage{amssymb}% <br>
\usepackage{hyperref}% <br>
\usepackage{rotating}% <br>
\usepackage[utf8x]{inputenc}% <br>
\usepackage[english,russian]{babel}% <br>
\usepackage{color}% <br>
\definecolor{red}{rgb}{1,0.1,0.1}% <br>
\definecolor{black}{rgb}{0,0,0}% <br>
\definecolor{white}{rgb}{1,1,1}% <br>
\definecolor{yellow}{rgb}{1,.93,0}% <br>
\definecolor{bluedark}{rgb}{0,0,.87}% <br>
\paperwidth  528pt% <br>
\paperheight 488pt% <br>
\topmargin -102pt% <br>
\oddsidemargin -78pt% <br>
\textwidth 610pt% <br>
\textheight 570pt% <br>
% <br>
\newcommand \sx {\scalebox}% <br>
\newcommand \ing {\includegraphics}% <br>
\newcommand \tet {\mathrm{tet}}% <br>
\newcommand \pen {\mathrm{pen}}% <br>
\newcommand \bC {\mathbb C}% <br>
\newcommand \fac {\mathrm {Factorial}}% <br>
\newcommand \rme {\mathrm e}% <br>
\newcommand \rmi {\mathrm i}% <br>
\newcommand \ds {\displaystyle}% <br>
\newcommand \rot {\begin{rotate}}% <br>
\newcommand \ero {\end{rotate}}% <br>
% <br>
\begin{document}% <br>
\parindent 0pt% <br>
\sx{4}% <br>
{\normalsize% <br>
\begin{picture}(155,122)% <br>
\put(0,0){\ing{tet10bx}}% <br>
%\put(-2,125){\sx{.7}{$y\!=\!{\rm tet}_{b}(x)$ ~as solution of~ $F(z\!+\!1)=\exp_b(F(z))$ ~,~ $F(0)\!=\!1$}}% <br>
%\put( 0,125){\sx{.55}{$y\!=\!F(x)$ ~as solution of~ $F(z\!+\!1)\!=\!\exp_b(F(z))$ ,~ $F(0)\!=\!1$}}% <br>
\put( 17,120){\sx{.6}{$y$}}% <br>
\put( 17,100){\sx{.6}{$8$}}% <br>
\put( 17,80){\sx{.6}{$6$}}% <br>
\put( 17,60){\sx{.6}{$4$}}% <br>
\put( 18,48){\sx{.6}{e}}% <br>
\put( 17,40){\sx{.6}{$2$}}% <br>
\put( 17,20){\sx{.6}{$0$}}% <br>
\put( 20.4,16){\sx{.6}{$0$}}% <br>
\put( 40.4,16){\sx{.6}{$2$}}% <br>
\put( 60.4,16){\sx{.6}{$4$}}% <br>
\put( 80.4,16){\sx{.6}{$6$}}% <br>
\put(100.4,16){\sx{.6}{$8$}}% <br>
\put(119,16){\sx{.6}{$10$}}% <br>
\put(128.6,16.2){\sx{.6}{$x$}}% <br>
%\put(2,90){\sx{.9}{$y\!=\!e\!\big(F_{1}(x\!+\!\rmi o)\big)$}}% <br>
%\put(183,105){\sx{1.}{$y\!=\!F_{3}(x)$}}% <br>
%\put(193,52){\sx{1.}{$y\!=\!\rme$}}% <br>
\put(26.6,86){\sx{.5}{\rot{90} $b\!\rightarrow\!\infty$ \ero } }% <br>
\put(31,106){\sx{.5}{\rot{88} $b\!=\!10$ \ero } }% <br>
%\put(39.2,106){\sx{.5}{\rot{86} $b\!=\! 3$ \ero } }% <br>
\put(42,87){\sx{.5}{\rot{87} $b\!=\! \rme$ \ero } }% <br>
\put(48.4,106){\sx{.5}{\rot{86} $b\!=\!2$ \ero } }% <br>
\put(53.3,106){\sx{.45}{\rot{85} $b\!=\!1.9$ \ero } }% <br>
\put(60.3,106){\sx{.45}{\rot{85} $b\!=\!1.8$ \ero } }% <br>
\put(68.4,106){\sx{.45}{\rot{84} $b\!=\!1.7$ \ero } }% <br>
\put(83,106){\sx{.45}{\rot{83} $b\!=\!1.6$ \ero } }% <br>
\put(128,106){\sx{.47}{\rot{80} $b\!=\!1.5$ \ero } }% <br>
%\put(55,88){\sx{1.3}{$y\!=\!\tet_b(x)$  } }% <br>
%\put(124,106){\sx{.6}{$b\!=\!1.5$}}% <br>
\put(109,46){\sx{.4}{\rot{2}$b\!=\!\exp(1/\rme)$\ero}}% <br>
\put(120,41.8){\sx{.34}{$b\!=\!\sqrt{2}$}}% <br>
\put(120,38){\sx{.36}{$b\!=\!1.4$}}% <br>
\put(120,33.6){\sx{.36}{$b\!=\!1.2$}}% <br>
%\put(115,29.6){\sx{.36}{$b\!=\!1.1$}}% <br>
\put(123,29){\sx{.36}{$b\!\rightarrow\!1$}}% <br>
\end{picture}}% <br>
\end{document}

References

↑ https://www.amazon.co.jp/Superfunctions-Non-integer-holomorphic-functions-superfunctions/dp/6202672862 Dmitrii Kouznetsov. Superfunctions: Non-integer iterates of holomorphic functions. Tetration and other superfunctions. Formulas,algorithms,tables,graphics ペーパーバック – 2020/7/28
↑ https://mizugadro.mydns.jp/BOOK/468.pdf Dmitrii Kouznetsov (2020). Superfunctions: Non-integer iterates of holomorphic functions. Tetration and other superfunctions. Formulas, algorithms, tables, graphics. Publisher: Lambert Academic Publishing.

https://www.morebooks.de/store/ru/book/Суперфункции/isbn/978-3-659-56202-0
http://www.ils.uec.ac.jp/!dima/BOOK/202.pdf
http://mizugadro.mydns.jp/BOOK/202.pdf Д.Кузнецов. Суперфункции. Lambert Academic Publishing, 2014. (In Russian), c.244, Рис. 17.1.

Keywords

«Book», «BookMap», «Hellmuth Kneser» «Maps of tetration», «Place of science», «Superfunction», «Superfunctions», «Tet2», «Tetration», «Tetration to base 2»,

File history

Click on a date/time to view the file as it appeared at that time.

	Date/Time	Thumbnail	Dimensions	User	Comment
current	17:50, 20 June 2013		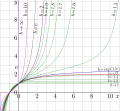2,192 × 2,026 (436 KB)	Maintenance script (talk \| contribs)	Importing image file

You cannot overwrite this file.

File usage

The following 8 pages use this file:

Metadata

This file contains additional information, probably added from the digital camera or scanner used to create or digitize it.

If the file has been modified from its original state, some details may not fully reflect the modified file.

Horizontal resolution	118.11 dpc
Vertical resolution	118.11 dpc

[1] ttps://www.amazon.co.jp/Superfunctions-Non-integer-holomorphic-functions-superfunctions/dp/6202672862 Dmitrii Kouznetsov. Superfunctions: Non-integer iterates of holomorphic functions. Tetration and other superfunctions. Formulas,algorithms,tables,graphics ペーパーバック – 2020/7/28

[2] ttps://mizugadro.mydns.jp/BOOK/468.pdf Dmitrii Kouznetsov (2020). Superfunctions: Non-integer iterates of holomorphic functions. Tetration and other superfunctions. Formulas, algorithms, tables, graphics. Publisher: Lambert Academic Publishing.

[1]

[2]

@@ Line 1: / Line 1: @@
+{{oq|Tetreal10bx10d.png|Original file ‎(2,192 × 2,026 pixels, file size: 436 KB, MIME type: image/png) }}
-Plot of [[Tetration]]:  $y=\mathrm{tet}_b(x)$ versus $x$ for
-: $b \rightarrow 1$,
-: $b = 1.1$,
-: $b = 1.2$,
-: $b = 1.3$,
-: $b = 1.4$,
-: $b = \sqrt{2}\approx 1.41,$
-: $b = \exp(1/ \mathrm e) \approx 1.44,$
-: $b = 1.5$,
-: $b = 1.6$,
-: $b = 1.7$,
-: $b = 1.8$,
-: $b = 1.9$,
-: $b = 2$,
-: $b = \mathrm e \approx 2.71$,
-: $b = 10$,
-: $b \rightarrow \infty$.
+[[Explicit plot]] of [[Tetration]]:  \(y=\mathrm{tet}_b(x)\) versus \(x\) for
-The fit is used, that provides several decimal digits, that seems to be sufficient to provide the "camera-ready copy";
+: \(b \rightarrow 1\),
-the errors of the fitting are not seen even at the zooming-in.
+: \(b = 1.1\),
+: \(b = 1.2\),
+: \(b = 1.3\),
+: \(b = 1.4\),
+: \(b = \sqrt{2}\approx 1.41,\)
+: \(b = \exp(1/ \mathrm e) \approx 1.44,\)
+: \(b = 1.5\),
+: \(b = 1.6\),
+: \(b = 1.7\),
+: \(b = 1.8\),
+: \(b = 1.9\),
+: \(b = 2\),
+: \(b = \mathrm e \approx 2.71\),
+: \(b = 10\),
+: \(b \rightarrow \infty\).
+The fit is used that provides several decimal digits: it is sufficient to make the "camera-ready copy"; the errors of the fitting are not seen even at the zooming-in.
-This image is used as figure 17.2 of book
-[[Superfunctions]]
+This image is used as figure 17.2 at page 239 of book «[[Superfunctions]]»
-<ref>https://www.morebooks.de/store/gb/book/superfunctions/isbn/978-620-2-67286-3 <br>
+<ref>
-http://mizugadro.mydns.jp/BOOK/466.pdf
+https://www.amazon.co.jp/Superfunctions-Non-integer-holomorphic-functions-superfunctions/dp/6202672862 Dmitrii Kouznetsov. Superfunctions: Non-integer iterates of holomorphic functions. Tetration and other superfunctions. Formulas,algorithms,tables,graphics ペーパーバック – 2020/7/28
-D.Kouznetsov. Superfunctions. [[Lambert Academic Publishing, 2020.
+</ref><ref>https://mizugadro.mydns.jp/BOOK/468.pdf Dmitrii Kouznetsov (2020). Superfunctions: Non-integer iterates of holomorphic functions. Tetration and other superfunctions. Formulas, algorithms, tables, graphics. Publisher: Lambert Academic Publishing.
 </ref>.
@@ Line 32: / Line 32: @@
 ==[[C++]] generator of curves==
-// Files [[GLxw2048.inc]], [[f2048ten.inc]], [[f4ten.cin]], [[fit1.cin]] should be loaded to the working directory in order to compile the [[C++]] code below:
+// Files [[GLxw2048.inc]], [[f2048ten.inc]], [[f4ten.cin]], [[fit1.cin]] should be loaded in order to compile the [[C++]] code below:
+<pre>
  #include <math.h>
  #include <stdio.h>
@@ Line 110: / Line 110: @@
  getchar(); system("killall Preview");// mac
  }
+</pre>
 ==[[Latex]] generator of labels==
+<pre>
-% File [[tet10bx.pdf]] sould  be generated with code above in order to compile the [[Latex]] document below % <br>
-%<poem><nomathjax><nowiki>
 \documentclass[12pt]{article} % <br>
 \usepackage{geometry} % See geometry.pdf % <br>
@@ Line 194: / Line 193: @@
 \end{picture}}% <br>
 \end{document}
+</pre>
-</nowiki></nomathjax></poem>
 ==References==
+{{ref}}
 https://www.morebooks.de/store/ru/book/Суперфункции/isbn/978-3-659-56202-0 <br>
 http://www.ils.uec.ac.jp/!dima/BOOK/202.pdf <br>
 http://mizugadro.mydns.jp/BOOK/202.pdf
-Д.Кузнецов. Суперфункции. [[Lambert Academic Publishing]], 2014. (In Russian), Figure 17.1.
+Д.Кузнецов. [[Суперфункции]]. [[Lambert Academic Publishing]], 2014. (In Russian), c.244, Рис. 17.1.
+<!--
+http://mizugadro.mydns.jp/BOOK/468.pdf
+D.Kouznetoov. [[Superfunctions]]. [[Lambert Academic Publishing]], 2020.
+!-->
+{{fer}}
+==Keywords==
+«[[Book]]»,
-http://mizugadro.mydns.jp/BOOK/466.pdf
+«[[BookMap]]»,
-D.Kouznetoov. Superfunctions. [[Lambert Academic Publishing]], 2020.
+<b>«[[Hellmuth Kneser]]»</b>
+<b>«[[Maps of tetration]]»</b>,
+<b>«[[Place of science]]»</b>,
+«[[Superfunction]]»,
+«[[Superfunctions]]»,
+<b>«[[Tet2]]»</b>,
+<b>«[[Tetration]]»</b>,
+<b>«[[Tetration to base 2]]»</b>,
 [[Category:Book]]
@@ Line 210: / Line 224: @@
 [[Category:C++]]
 [[Category:Explicit plot]]
+[[Category:Hellmuth Kneser]]
 [[Category:Latex]]
+[[Category:Mathematical function]]
 [[Category:Mathematical functions]]
-[[Category:Michael Moldenhauer]]
+[[Category:Superfunction]]
 [[Category:Tetration]]
+<!--
+[[Category:Michael Moldenhauer]] ??
 [[Category:Real-real plots]]
+!-->