Difference between revisions of "ArcTania"
Jump to navigation
Jump to search
m (Text replacement - "\$([^\$]+)\$" to "\\(\1\\)") |
|||
| Line 1: | Line 1: | ||
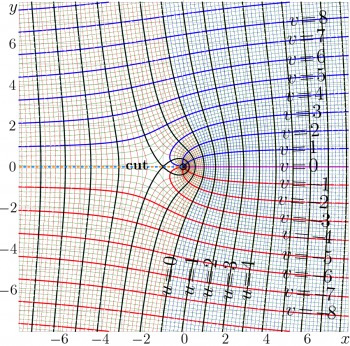
| − | [[File:ArcTaniaMap.png|right|350px|thumb| |
+ | [[File:ArcTaniaMap.png|right|350px|thumb| \(f=\mathrm{ArcTania}(x\!+\!{\rm i} y)\) in the \(x,y\) plane with levels |
| − | + | \(u\!=\!\Re(f)\!=\! \mathrm {const} ~\) and |
|
| − | + | \(v\!=\!\Im(f)\!=\! \mathrm {const} ~\)]] |
|
[[ArcTania]] is [[elementary function, |
[[ArcTania]] is [[elementary function, |
||
| − | + | \(\mathrm{ArcTania}(z)=z+\ln(z)−1\) |
|
[[Complex map]] of [[ArcTania]] is shown in figure at right. |
[[Complex map]] of [[ArcTania]] is shown in figure at right. |
||
| − | [[ArcTania]] is important, because its inverse function |
+ | [[ArcTania]] is important, because its inverse function \(\mathrm{Tania}=\mathrm{ArcTania}^{-1}\) , is est, the [[Tania function]], |
appears in the [[Laser science]] as solution of the equation of evolution of intensity of light in the idealised saturable amplifier |
appears in the [[Laser science]] as solution of the equation of evolution of intensity of light in the idealised saturable amplifier |
||
<ref> |
<ref> |
||
| Line 17: | Line 17: | ||
</ref>: |
</ref>: |
||
| − | + | \( \displaystyle \mathrm{Tania}^{\prime}(z)=\frac{\mathrm{Tania}(z)}{1+\mathrm{Tania}(z)} \) |
|
==References== |
==References== |
||
Latest revision as of 18:43, 30 July 2019
ArcTania is [[elementary function,
\(\mathrm{ArcTania}(z)=z+\ln(z)−1\)
Complex map of ArcTania is shown in figure at right.
ArcTania is important, because its inverse function \(\mathrm{Tania}=\mathrm{ArcTania}^{-1}\) , is est, the Tania function, appears in the Laser science as solution of the equation of evolution of intensity of light in the idealised saturable amplifier [1]:
\( \displaystyle \mathrm{Tania}^{\prime}(z)=\frac{\mathrm{Tania}(z)}{1+\mathrm{Tania}(z)} \)
References
- ↑
http://link.springer.com/article/10.1007/s10043-013-0058-6
http://mizugadro.mydns.jp/PAPERS/2013or1.pdf
http://mizugadro.mydns.jp/PAPERS/2013or2.pdf D.Kouznetsov. Superfunctions for amplifiers. Optical Review, July 2013, Volume 20, Issue 4, pp 321-326.