Tania function

Comparison of Tania function (thin curve) to the Shoka function (thick curve) for real values of the argument

\(f=\mathrm{Tania}(x\!+\!{\rm i} y)\) in the \(x,y\) plane with levels \(u\!=\!\Re(f)\!=\! \mathrm {const} ~\) and \(v\!=\!\Im(f)\!=\! \mathrm {const} ~\)

Tania function is solution \(f\!=\!\mathrm{Tania}\) of equation

\(\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\! \displaystyle (1) ~ ~ ~ f'(z)= \frac{f(z)}{1+f(z)} \)

with initial condition

\(\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\! \displaystyle (2) ~ ~ ~ f(0)=1 \)

The contour of integration of equation (1) goes from zero to the imaginary part of \(z\) along the imaginary axis and then along the straight line (parallel to the real axis) to the point \(z\). The contour of integration of equation (1) can be modified without to affect the values of the function, but it should not intersect the cut lines \( \Re(z)\!<\!-1\), \(\Im(z)\!=\!\pm \pi\). In particular, for the real values of the argument, the integration of (1) from 0 to \(z\) can be performed along the real axis. Properties of Tania function are described in scientific journal Optical Review .

Relation to other special functions

\(f=\mathrm{ArcTania}(x\!+\!{\rm i} y)\) in the \(x,y\) plane with levels \(u\!=\!\Re(f)\!=\! \mathrm {const} ~\) and \(v\!=\!\Im(f)\!=\! \mathrm {const} ~\)

At moderate values of the imaginary part of the argument, say, \(|\Im(z)|\!<\!\pi\), the Tania function can be expressed through the LambertW function as follows:

\( \mathrm{Tania}(z)=\mathrm{LambertW}(\exp(z\!+\!1))\)

Also, the Tania function is related to the WrightOmega function,

\( \mathrm{Tania}(z)=\mathrm{WrightOmega}(z\!+\!1)\)

and, as the WrightOmega function can be used for the "unfolding" of the LambertW function.

Tania function has two branch points: \(~ -\!2\!\pm\! \mathrm i \pi~\). The position of the cut lines depends on the representation. In TORI the cut lines are directed to the left, parallel to the real axis.

The resources for Tania function can be reached through http://www.ils.uec.ac.jp/~dima/e/Tania

After to load the article, it happened that similar function is known by the other name WrightOmega Function .

\(\mathrm{WrightOmega}(z)=\mathrm{Tania}(z\!-\!1)\)

However, neither algorithm for the evaluation not complex maps of the WrightOmega are suggested there. Name WrightOmega seems to be too long; for this reason, in TORI, perhaps, both names will be used. More literature about the WrightOmega function can be found in the preprint by Corless and Jeffery .

The branches of the LambertW function can be expressed through the WrithtOmega function or through the Tania function in the following way :

\( \mathrm{LambertW}_k(z)=\mathrm{WrightOmega} \Big( \ln(z)+2 \pi \mathrm i k \Big) = \mathrm{Tania} \Big( \ln(z)+2 \pi \mathrm i k + 1 \Big)\)

at least for integer values of \(k\).

ArcTania

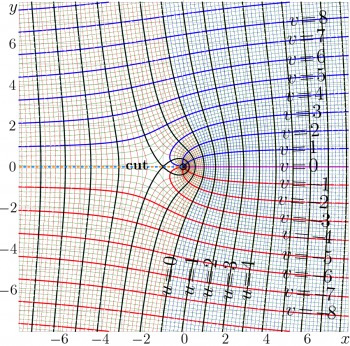
Let ArcTania be the inverse function of Tania; id est, \(\mathrm{ArcTania}=\mathrm{Tania}^{-1}\). The ArcTania can be expressed in terms of the elementary functions:

\(\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\! \displaystyle (3) ~ ~ ~ \mathrm{ArcTania}(z)=z+\ln(z)-1\)

The expression (3) is valid for \(z\in \mathbb C \backslash \{z\in \mathbb R, z\le 0 \}\).

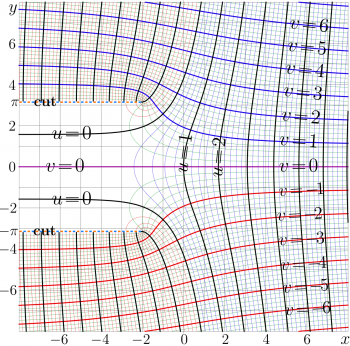
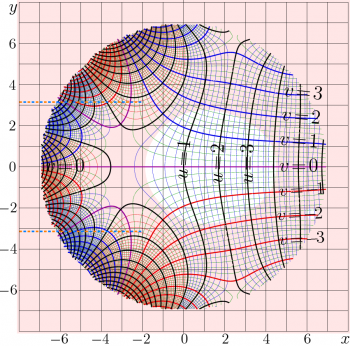
The complex maps of the ArcTania and Tania functions are shown in the figures at right. \(f=\mathrm{Tania}(x\!+\!\mathrm{i} y)\) and \(f=\mathrm{ArcTania}(x\!+\!\mathrm{i} y)\) are shown in the \(x,y\) plane with levels
\(u\!=\!\Re(f)\!=\! \mathrm {const} ~\) and
\(v\!=\!\Im(f)\!=\! \mathrm {const} ~\).

ArcTania by equation (3) is elementary function; so, the Tania could be defined also as the inverse function of ArcTania with equations

\(\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\! \displaystyle (4\mathrm{a}) ~ ~ ~ \mathrm{Tania}(\mathrm{ArcTania}(z))=z~\) for all \(z\) except \(z\le 0\)

or

\(\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\! \displaystyle (4\mathrm{b}) ~ ~ ~ \mathrm{ArcTania}(\mathrm{Tania}(z))=z~\) for all \(z\) except \(\Im(z)=\pm \mathrm{i} \pi, \Re(z)\le -2\)

Properties of Tania and ArcTania

The \(\mathrm{Tania}(z)\) has two cut lines, \(\Im(z)=\pm \pi~\), \(~\Re(z)\le-2\). In the figure, these lines are marked with dashed half-lines. The branch points are determined by the singularity of the expression in the right hand side of equation (1), they correspond to values of ArcTania at \(-1=\exp(\pm \mathrm i \pi)\). Using (3), these points can be expressed as follows:

\(z_{\pm}=\exp(\pm \mathrm i \pi) +\ln(\exp(\pm \mathrm i \pi)) -1=-2\pm \mathrm i \pi~\).

In order to simplify the expansion at the branchpoints (see below), the cut lines are directed to the left, parallel to the real axis. (In the similar way the direction of the cut lines is chosen for the ArcTetration to the real base larger than \(\exp(1/\mathrm{e})\). )

In the left hand side of the complex map, between the cut lines lines, the Tania function exponentially approaches zero. In other directions outside this strip, the modulus of the function is smoothly growing; the growth is similar to that of the linear function.

Tania is real–holomorhic;

\( \mathrm{Tania}(z^*)=\mathrm{Tania}(z)^*\)

The expansions of Tania in diffrent cases, and, in particular, at the branchpoints \(z_\pm\) is described below.

Expansion of Tania at infinity

Complex map of the truncated function by (7a)

The complex maps of Tania and ArcTania above show that asymptotically each of these functions becomes similar to its argument. Being far from the branch points (and outside the cut lines), the grid of the lines of constant real and constant imaginary part looks similar to that of the identity function. This indicates that the leading term of the expansion at infinity of \(\mathrm{Tania}(z)\) should be just \(z\). Such an expansion is suggested in this section.

At large values of the argument, Tania shows almost linear growth and can be expanded as follows:

\(\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\! \displaystyle (7) ~ ~ ~ \mathrm{Tania}(z)=\) \(\displaystyle z + 1\!-\!\ln(z) +\frac{ \ln(z)\!-\!1}{z} \) \(\displaystyle +\frac{\ln(z)^2-4\ln(z)+3}{2z^2} \) \(\displaystyle +\frac{2 \ln(z)^3 - 15 \ln(z)^2 + 30 \ln(z) -17}{ 6 z^3} \) \(\displaystyle + O\Big( \frac{\ln(z)}{z}\Big)^4 \)

At \(|z|\gg 1\), the truncated series (7) can be used for the evaluation of \(\mathrm{Tania}(z)\), while the argument is not between the cut lines in figure. For the evaluation, the asymptotic can be written also as follows:

\(\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\! (7\mathrm{a}) ~ ~ ~ \mathrm{Tania}(z)=\) \(\displaystyle (z\!+\!1)\!-\!\ln(z\!+\!1) +\frac{ \ln(z\!+\!1)}{z+1}\) \(\displaystyle +\Big(\frac{ \ln(z\!+\!1)}{z+1}\Big)^{\!2} \Big(\frac{1}{2}-\ln(z\!+\!1)^{-1}\Big)\) \(\displaystyle +\Big(\frac{ \ln(z\!+\!1)}{z+1}\big)^{\!3} \Big( \frac{1}{3}-\frac{3}{4} \ln(z\!+\!1)^{-1}+ \ln(z\!+\!1)^{-2}\big)\) \(\displaystyle +\Big(\frac{ \ln(z\!+\!1)}{z+1}\Big)^{\!4} \Big( \frac{1}{4}-\frac{11}{\!5} \ln(z\!+\!1)^{-1}+3\ln(z\!+\!1)^{-2}-\ln(z\!+\!1)^{-3}\Big)\) \(\displaystyle + O\Big( \frac{\ln(z\!+\!1)}{z+1}\Big)^{\!5} \)

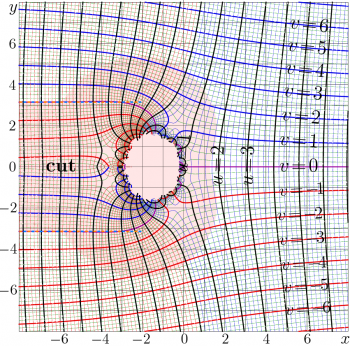
Such an expression shows that the effective small parameter of the expansion is \(\displaystyle \frac{\ln(z\!+\!1)}{z+1}\). The complex map of the truncation of expression in the right hand side of (7a) is plotted in the figure at right in the same notations as in the previous figure. In the shaded range, the precision of the approximation is less than 3; outside that region, the truncated series with the last term of order of \(\displaystyle \Big( \frac{\ln(z\!+\!1)}{z+1}\Big)^4\) return more than 3 significant decimal digits. The precision of any approximation is evaluated as follows:

\(\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\! (7\mathrm{b}) ~ ~ ~ \mathrm{Precision}(z)=\) \( \displaystyle - \lg\big( \frac{ |\mathrm{Tania}(z)-\mathrm{approximation}(z)|} { |\mathrm{Tania}(z)|+|\mathrm{approximation}(z)|} \big) \)

In such a way, outside the shaded range, the truncated series (7a) provides at least 3 significant decimal digits.

Asymptotic expansion of Tania between the cut lines

Complex map of truncation of series (8)

The expansions (7) and (7a) are not valid between the cut lines. For this range, for large values of the argument, the special expansion is suggested in this section.

For \(-\Re(z)\!\gg \! 1\) at \(|\Im(z)| \!<\! \pi\), the solution \(f\) of the Tania equation can be expanded as follows:

\(\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\! \displaystyle (8) ~ ~ ~ f(z) ~\sim~\) \(\varepsilon -\varepsilon^2+\frac{3}{2}\varepsilon^3 -\frac{8}{3}\varepsilon^4+\frac{125}{24}\varepsilon^5+ O(\varepsilon^6) \)

where \(\varepsilon=\exp(1\!+\!z)\).

Such expansion can be obtained iterating assignment

\(f=\varepsilon \exp(-f)\)

with the initial approach \(f=\varepsilon + O(\varepsilon^2)\).

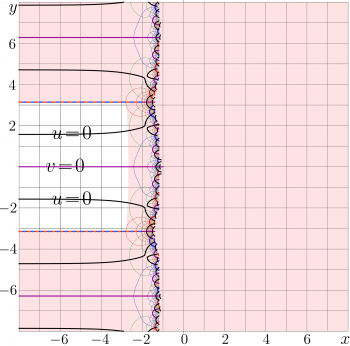
The example of the truncated series is shown in figure at right. The same notations for the complex map are used. In the shaded region, the precision is less than 3. In particular, the expansion (8) does not approximate \(\mathrm{Tania}(z)\) at \(\Re(z)\!>\!-2~\). However, the truncated series can be used for the precise evaluation of \(\mathrm{Tania}(z)\) at \(\Re(z)<-3\), \(\Im(z)<\pi\).

Together with the expansion (7a), the expansion (8) covers the most of the complex plane, leaving only a finite-size domain that includes the branch points and the origin of the coordinates. The expansion at these points are considered below.

Expansion of Tania at singularities

Complex map of approximation by (10)

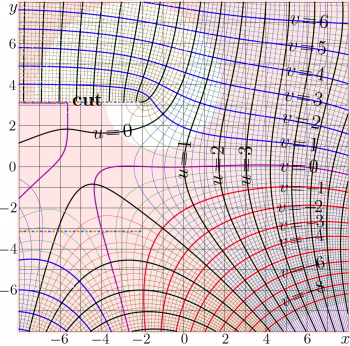
\(\mathrm{Tania}(z)\) has two cut lines at \(\Re(z)\!\le\! -2\), \(\Im(z)\!=\!\pm \pi\). The expansions above do not reproduce the behavior of Tania in vicinity of the branch points. In this section, the expansion at these branch points is suggested.

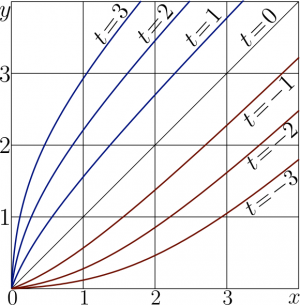
For the expansion of \(\mathrm{Tania}(z)\) at the upper branch point \(z=-2+\pi \mathrm i\), the convenient small parameter is

\( \!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\! (9) ~ ~ ~ t= \mathrm{i} \sqrt{ \frac{2}{9} (z+2-\pi \mathrm i )~} \)

then, the expansion of Tania can be written as follows:

\(\displaystyle \!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\! (10) ~ ~ ~ \mathrm{Tania}(z)=\) \( -1+3t-3t^2\) \( +\frac{3}{4} t^3\) \( +\frac{3}{10}t^4\) \( +\frac{9}{160}t^5\) \( -\frac{3}{70}t^6\) \( -\frac{1251}{22400} t^7 \) \( -\frac{9}{280} t^8+...\)

The Mathematica Series routine easy calculates some tens of the first coefficients of the expansion. The series seems to converge while \(|z\!+2\!-\!\pi \mathrm i |\! <\! 2\pi\); in vicinity of another branch point, id est, at \(z\approx -2\!-\!\mathrm{i}\), such an approximation is not valid.

The figure at right shows complex map of the truncated series by (10) in the same notations as in the previous maps. The shaded region indicate the domain where the precision of the approximation is less than 3; in the white spot the the approximation by the polynomial of 5th order with respect to \(t\) gives at least three significant figures.

In vicinity of the origen of coordinates, for example, at \(-4\!<\!z\!<\!6\), the truncated series (with term of order of \(t^9\) and higher dropped) provides of order of 2 decimal digits, and the deviation of line \(v\!=\!0\) from the abscissa axis is barely seen in the figure.

Similar expansion of Tania at point \(-2-\pi \mathrm i\) can be obtained by complex conjugation of expressions (9) and (10).

Taylor expansions of Tania

Map of the truncated expansion (11) in the same notations

The expansions above, in principle, allow to cover all the complex plane with the approximations of the Tania function. But the expansion at the branch points may be not convenient while dealing with Tania of a real argument. For this case, the Taylor expansions of Tania at the real axis are suggested in this section.

The Taylor expansion of Tania at zero

\(\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\! \displaystyle (11) ~ ~ ~ \mathrm{Tania}(z)=\) \(1 \) \( +\frac{z}{2}\) \( +\frac{z^2}{16}\) \( -\frac{z^3}{192}\) \( -\frac{z^4}{3072}\) \( +\frac{13 z^5}{61440}\) \( -\frac{47 z^6}{1474560}\) \( +\frac{73 z^7}{41287680}\) \( + ... \)

converges at \(|z|<\sqrt{4+\pi^2}\approx 3.724\); this series can be obtained with the Mathematica's operator InverseSeries, converting the expansion

\(\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\! \displaystyle (12) ~ ~ ~ \mathrm{ArcTania}(z)=\) \( 2(z\!-\!1)\) \( -\frac{(z\!-\!1)^2}{2}\) \( +\frac{(z\!-\!1)^3}{3}\) \( -\frac{(z\!-\!1)^4}{4}\) \( +\frac{(z\!-\!1)^5}{5}\) \( +\frac{(z\!-\!1)^6}{6}\) \( +~ {O}(z\!-\!1)^7\)

However, more terms can be added to the series in (11) and (12). At moderate values of \(|z|\lesssim 1\), the exansion (11) can be used for the efficient (quick and precise) evaluation of \(\mathrm{Tania}(z)\); in order to get 14 significant decimal digits, it is sufficient to take 20 terms.

The complex map of the truncated expansion (11) as polynomial of 7th power of \(z\) is shown in figure at right for \(|z|\!<\!7\). The range where such an approximation of \(\mathrm{Tania}(z)\) gives less than 3 significant figures is shaded. The same notations as in the previous figures are used.

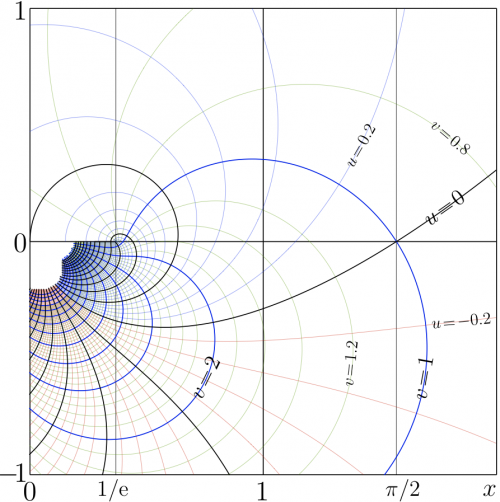
In the similar way, the expansion of \(\mathrm{Tania}(z)\) at \(z=-2+1/\mathrm e\approx -1.632\) can be written as follows:

\(\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\! \displaystyle (13) ~ ~ ~ \mathrm{Tania}(z)=\) \( \frac{1}{\mathrm{e}} \) \( + \frac {1/\mathrm{e}} {1+1/\mathrm{e}}\) \(\big(z+2-\frac{1}{\mathrm{e}}\big) \) \( + \frac{1/\mathrm{e}}{2(1+1/\mathrm{e})^3} \big(z+2-\frac{1}{\mathrm{e}}\big)^2\) \( + \frac{(1-2/\mathrm{e})/\mathrm{e}}{6(1+1/\mathrm{e})^5} \big(z+2-\frac{1}{\mathrm{e}}\big)^3+...\)

The series converges at \(\big|z+2-\frac{1}{\mathrm{e}}\big|\) \(<\) \(\sqrt{\pi^2+1/\mathrm{e}^2} \approx 3.1445~\).

The truncated expansions above cover all the complex plane with at least 3–digit approximations.

Evaluation of Tania function

The series above can be used for the evaluation of \(\mathrm{Tania}(z)\), dependently on value of \(z\). The increase of the precision of the evaluation is easier to achieve not with the increase of number of terms in the expansion, but applying the Newton method. Let \(s_0\) be initial approximation, obtained with the appropriate formulas from the set above; let

\( \displaystyle \!\!\!\!\!\!\!\!\!\! (14) ~ ~ ~ s_{n+1}=s_n + \frac{z-\mathrm{ArcTania}(s_n)}{\mathrm{ArcTania}'(s_n)}\)

where

\( \displaystyle \!\!\!\!\!\!\!\!\!\! (15) ~ ~ ~\mathrm{ArcTania}'(z)=1+1/z\)

is derivative of the ArcTania function by equation (3). The primary approximations considered in the previous sections allow to get good initial approximation for any point of the complex plane; then the sequence \(s\) converges to \(\mathrm{Tania}(z)\).

The sequence \(s\) converges faster than exponentially. Practically, of order of 5 terms in some of the primary approximations are sufficient, and then the third iteration \(s_3\) approximates \(\mathrm{Tania}(z)\) with 15 decimal digits. Working with the "complex double" variables, the precision cannot be better. In such a way, the Tania function is implemented in C++. Few tens elementary operations are sufficient to get the maximal precision available; all the graphics can be plotted in the real time with the generators supplied. (Click the figure to see the implementation.)

Relation to the LambertW function

In certain range of values of the argument, the Tania function can be expressed through the LambertW function, known also as ProductLog , as follows:

\(\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\! \displaystyle (16) ~ ~ ~ \mathrm{Tania}(z)=\mathrm{ProductLog}(\exp(1\!+\!z))\) for \(z \in \mathbb C : |\Im(z)|\!<\! \pi\)

The LambertW function can be expressed through the Tania function

\( \!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\! \displaystyle (17) ~ ~ ~ \mathrm{ProductLog}(z)=\mathrm{Tania}(\ln(z)-1)\)

for all complex \(z\) except negative part of the real axis. Function LambertW is built-in in many programing languages such as Mathematica, Maple, Matlab. In Mathematica, function LambertW is called also "ProductLog".

The equation for the LambertW function is similar to (1):

\( \!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\! \displaystyle (18) ~ ~ ~ \mathrm{LambertW}'(z) =\frac{\mathrm{LambertW}(z)}{(1+\mathrm{LambertW}(z))~z}\)

However, the explicit dependence on \(z\) of the right band side of the equation beaks the translational invariance of the solution and makes the evaluation of the LambertW function more complicated than the evaluation of the Tania function. In such a way, the Tania function can be used for the evaluation of the LambertW function.

Historically, properties of LambdaW functions were described before those of the Tania function. On the other hand, the equation for the Tania function is easier than that for the LambertW function, and behavior of Tania function is simpler than that of the LambertW. Therefore, in TORI, the Tania function is considered as more fundamental than the LambertW; and the LambertW is implemented through Tania, and not Tania through the Lambert W. However, at small values of the imaginary part of the argument and programming in the languages, where the LambertW is already implemented, the representation of Tania function through the LambertW also can be used.

History and applications

The Tania function appears as the intensity of light in the informly pumped gain medium, measured in unit of the saturation intensity. Then, its argument has sense of length of propagation, measured in units of the inverse of unsaturated gain. Such a model describes the idealized laser amplifier with simplest kinetics, and can be applied, for example, to the Yb-doped ceramics pumped in vicinity of wavelength of order of 940nm; then the maximum gain corresponds to wavelength in vicinity of 1030 nm. Then, the saturation intensity may have value of order of \(I_{\rm sat}=100 {\rm W/mm}^2\), and the unsaturated gain, dependently on the concentration of dopant and the intensity of pump, may be of order of \(g_0 \approx 1/\mathrm{mm}\) . This determines the orders of magnitude of values of the physical parameters, while the intensity along the propagation at distance \(x\) can be described with intensity \(I(x)\) satisfying the equation

\( \!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\! \displaystyle (19) ~ ~ ~ I'(x)= \frac{ g_0 I(x) }{1+I(x)/I_{\rm sat}} \)

The solution \(I\) can be expressed as

\( \!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\! \displaystyle (20) ~ ~ ~ I(x)=I_{\rm sat} \mathrm{Tania}( g_0 x - g_0 x_1)\)

where \(x_1\) is distance at which the intensity saturates the gain, id est, \(I(x_1)=I_{\rm sat}\).

The phenomenology of phenomena with such a saturated gain is considered in century 20; some results are published in the Soviet Journal of Quantum Electronics . The function "Tania" is named after the short name of the first author of . It seems that in years 1980s, she did not know about works by E.M.Wright ; so, this function and similar functions were calculated numerically.

Doya function

\(y\!=\!\mathrm{Doya}^t(x))\) for various \(t\)

The Doya function can be defined in terms of theTania function and its inverse,

\( \displaystyle \!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\! (21) ~ ~ ~ \mathrm{Doya}_t(z)= \mathrm{Tania}(t+\mathrm{ArcTania}(z)) \)

where \(t\) is real parameter.

The Tania function can be evaluated using the Doya function and the regular iteration at the fixed point \(0\), as \(\mathrm{Doya}_t(0)\!=\!0\). The same method can be applied also to other transfer functions, even if they cannot be easy represented through the special functions. This may refer, for example, to the experimentally–measured transfer function, that has no need to coincide with the Doya function.

In the simple model of a nonlinear amplifier, the transfer function can be expressed in terms of the Doya function as follows:

\( \displaystyle \!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\! (22) ~ ~ ~ T(z)= P_{\rm sat} \mathrm{Doya}_t(z/P_{\rm sat})\)

where \(P_{\rm sat}\) is the saturation power; roughly the product of \(I_{\rm sat}\) and the area of cross-section of the active region. In this case, \(t\) has sense of the unsaturated gain at the length of the amplifier. The negative values correspond to the saturable absorber.

In such a way, in this model, the transfer function is determined by the two parameters \(P_{\rm sat}\) and \(t\) through the known functions Doya and Tania.

Fixed points of the logarithm to the complex base

Complex map of function Filog

The generalization of tetration to the complex base is assumed to converge to the two fixed points of logarithm in the upper and the lower parts of the complex plane (as the imaginary part of the argument becomes infinite). These fixed points are expressed with the function Filog; \(f=\mathrm{Filog}(a)\) is solution of the equation

\( \displaystyle \log_b(f)=f\)

where \(b=\exp(a)\).

The Filog function can be expressed through the Tania function as follows:

\(\displaystyle \mathrm{Filog}(z)= \frac{\mathrm{Tania}\!\big(\ln(z)-1-\mathrm{i}\big)}{-z} = \frac{\mathrm{WrightOmega}\!\big(\ln(z)-\mathrm{i}\big)}{-z}\)

The complex map of \(f=\mathrm{Filog}(x+\mathrm i y)\) is shown at the figure at right in the \(x,y\) plane with levels \(u\!=\!\Re(f)=\mathrm{const}\) and levels \(u=\Im(f)=\mathrm{const}\).

Then, the tetration to base \(b\!=\!\exp(a)\) should have the following properties:

\(\displaystyle \lim_{y\rightarrow +\infty}\) \(\mathrm{tet}_b(x+\mathrm i y)= \mathrm{Filog}(a)\)

\(\displaystyle \lim_{y\rightarrow -\infty}\) \(\mathrm{tet}_b(x+\mathrm i y)= \mathrm{Filog}(a^*)^*\)

Such a conjecture seems to give way to the correct definition of the tetration to the complex base.

Conclusions

Tania function came from the Laser science, it describes the amplification of light in a gain medium with the simple kinetics. The inverse of Tania function is elementary function.Tania function is superfunction with respect to the Doya function.

There is some analogy with the Yulya function, but in that case, the ArcYulya is elementary function, while the Yulya function cannot be simply expressed in term the primary elementary functions. There is certain voluntarism in decision, which function in the pair (function, its inverse) gets the name of its first users, letting the name of the inverse function to have prefix "Arc". While the terms Yulya function and and Doya function and Tania function are not yet widely used, now is good time to express any objections or suggestions with respect to the naming of these functions.

Keywords

Doya function, LambertW function, Laser science, Superfunction, Transfer equation, Transfer function