LambertW function
LambertW, called also ProductLog[1], is solution \(W=W(z)\) of equations
- \( \displaystyle \!\!\!\!\!\!\!\!\!\!\!\!\!\!\! (0\mathrm{a}) ~ ~ ~ W'= \frac{W}{(1+W)~z}\)
- \( \displaystyle \!\!\!\!\!\!\!\!\!\!\!\!\!\!\! (0\mathrm{b}) ~ ~ ~ W(0)=0\)
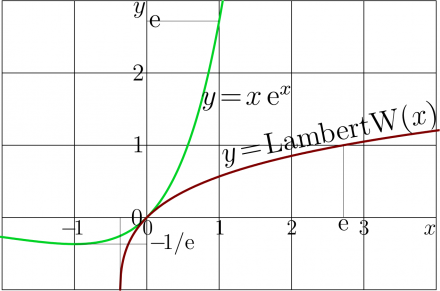
The cut line is drawn from the singularity at \(-1/\mathrm e\) to \(-\infty\).
Relation with other functions
LambertW is the the inverse function of ArcLambertW. In TORI, ArcLambertW is denoted also as zex, which is shortening of writing z multiplied by exponent of z. Such a shortening is used in order to simplify creation of such names as SuZex (superfunction of zex) and AbelZex (Abel function of zex).
ArcLambertW is defined with
- \( \displaystyle \!\!\!\!\!\!\!\!\!\!\!\!\!\!\! (1) ~ ~ ~ \mathrm{ArcLambertW}(z)=z \cdot \exp(z)\)
ArcLambertW is entire function; for the real values of the argument, its explicit plot is shown in figure at right.
LambertW is Holomorphic function at the whole complex plane except half-line along the negative part of the real axis, id est, the domain of the holomorphism is \(\mathbb C \backslash \{ x\in \mathbb R : x\le -1/\mathrm{e} \}\).
The Mathematica makes no difference between LambdaW function and ProductLog in the expressions; these are supposed to be different names of the same function [1].
If the ProductLog or LambertW appears with two arguments, then the first of them is supposed to be integer number, indicating the branch of the function, extended beyond the cut \(z\in \mathbb R : x \le -1/\mathrm e\). The principal branch is assigned number zero, LambertW[0,z]=LambertW[z].
LambertW function is related to the Tania function and the WrightOmega
- \( \mathrm{Tania}(z)=\mathrm{LambertW}\Big(\exp(1\!+\!z)\Big)~\), \(~\mathrm{WrightOmega}(z)=\mathrm{LambertW}\Big(\exp(z)\Big)~~\), \(~|\Im(z)|\!<\!\pi\)
- \( \mathrm{LambertW}(z)=\mathrm{Tania}\Big(\ln(z)-1\Big)=\mathrm{WrightOmega}\Big(\ln(z)\Big)\)
which has applications in the laser science. In the simple model of an optical amplifier, the transfer function is Doya, which and can be expressed through the LambertW as follows:
- \( \mathrm{Doya}_t(z)=\mathrm{LambertW}\big( z~ \mathrm{e} ^{z+t} \big)\)
at least for moderated values \(|\Im(z)|\!<\!\pi\).
Properties of ArcLambertW
ArcLambertW is real entire function; the expansion at zero follows from the expansion of the exponential,
- \( \displaystyle \!\!\!\!\!\!\!\!\!\!\!\!\!\!\! (4) ~ ~ ~ \mathrm{ArcLambertW}(z)=z+z^2+z^3/2+z^4/3!+z^5/4! ~+~ ...\)
Along the real axis, \(\mathrm{ArcLambertW}(x)\) monotoincally decreases from zero at \(x\!=\! - \infty\) to \(-1/\mathrm{e}\) at \(x\!=\!-1\), has minimum at \(x\!=\!-1\), and monotonically increases at \(x\!\ge\! -1\).
Accodringly, \(\mathrm{LambertW}(z)\) has branchpoint at \(z\!=\!-1/\mathrm e\).
Properties of LambertW
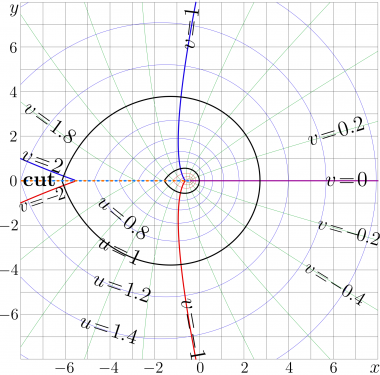
The complex map of the LambertW is shown at figure at right. Let \(f=\mathrm{LambertW}(x\!+\!\mathrm i y)\); then, the lines of constant \(u\!=\!\Re(f)\) and the lines of constant \(v\!=\!\Im(f)\) are drawn in the \(x,y\) plane. The thick lines correspond to the integer values. The cut line corresponds to \(x\!\le\! - 1/\mathrm{e}\). The representation through the Tania function is used to plot the figure.
Small argument
The expansion at zero can be written inverting series (4) above:
- \(\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\! (5) ~ ~ \mathrm{LambertW}(z)=\) \(\displaystyle z\sum_{n=0}^{\infty} \frac{(n\!+\!1)^{n-1}}{n!} (-z)^n =\) \(\displaystyle z-z^2 +\frac{3 z^3}{2}\) \(\displaystyle -\frac{8z^4}{3}\) \(\displaystyle +\frac{125z^5}{24}\) \(\displaystyle -\frac{54 z^6}{5}\) \(\displaystyle +\frac{16807 z^7}{720} +... \)
The series converges at \(|z|\!<\! 1/\mathrm{e} \!\approx\! 0.367879~\). With 48 terms, at \(|z|\!\le 0.2\), the sum provides at least 16 correct decimal digits.
Near \(-1/\mathrm e\)
The expansion at of the branch point can be written as follows:
- \(\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\! (6)\displaystyle ~ ~ ~ \mathrm{LambertW}\Big(\frac{-1}{\mathrm e} + \frac{t^2}{2\mathrm e}\Big)= \) \(-1 +t\) \(\displaystyle -\frac{t^2}{3}\) \(\displaystyle +\frac{11 t^3}{72}\) \(\displaystyle -\frac{43 t^4}{540}\) \(\displaystyle +\frac{769 t^5}{17280}\) \(\displaystyle - \frac{221 t^6}{8505}\) \(\displaystyle +\frac{680863 t^7}{43545600}\) \(\displaystyle -\frac{1963 t^8}{204120}\) \(\displaystyle +\frac{226287557 t^9}{37623398400}\) \(\displaystyle -\frac{5776369 t^{10}}{1515591000} +..\)
The expansion can be used for approximation of LambertW while \(|t|\!<\!1\), id est, while the argument of LambertW is close to \(-\exp(-1)\!\approx\! -0.367879~\).
Large argument
For large values of \(|z|\), using notations \(L\!=\ln(z)\) and \(M\!=\!\ln^2(z)\) the expansion of \(\mathrm{LambertW}(z)\) can be written as follows:
- \(\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\! (8) ~ ~ \mathrm{LambertW}(z)= \) \(\displaystyle L - M +\frac{M}{L} +\frac{M(-2+M)}{2L^2} \) \(\displaystyle +\frac{M(6-9M+2M^2)}{6L^3}\) \(\displaystyle +\frac{M(-12+36M-22M^2+3M^3)}{12 L^4}\) \(\displaystyle +\frac{M(60-300M+350M^2-125M^3+12M^4)}{60L^5}\) \(\displaystyle +\frac{M(-120+900M-1700M^2+1125M^3-274M^4+20 M^5)}{120L^6}\) \(\displaystyle +O\Big( \frac{M}{L} \Big)^7\)
where the effective parameter of expansion seems to be \(\varepsilon=\ln^2(z)/\ln(z)\); at \(|\varepsilon|\ll 1\), the asymptotics (8) can be used for the evaluation of LambertW.
In (8), as in other articles in TORI, the upper superscript after the function indicates the number of iterations, and the upper superscript after the argument and the closing parenthesis indicates the power that is assumed to be evaluated after the evaluation of the function. However, \(\ln^{-1}(z)=\exp(z)\) should not be confused with \(1/\ln(z)\), nor \(\ln^{2}(z)=\ln(\ln(z))\) should be confused with \(\ln(z)^2\), and so on.
Approximation of LambertW
In many cases, the series of expansion of LambertW converge slowly, if at all. For the evaluation of LambertW, it can be expressed through the Tania function:
- \(\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\! (9) ~ ~ \mathrm{LambertW}(z)= \mathrm{Tania}(\ln(z)-1)\)
This representation is good in the whole complex plane except the negative part of the real axis. Such a representation is used to plot the complex map shown in the figure. For evaluation between \(-1/\mathrm e\) and 0, the generator of the explicit plot of LambertW at the top uses the expansions (5) and (6) above; their implementations can be loaded from the figure. (I could not make the special numerical implementation for LambertW better than that through the Tania function, it is fast and precise.)
References
- ↑ 1.0 1.1
http://mathworld.wolfram.com/LambertW-Function.html
Weisstein, Eric W. "Lambert W-Function." From MathWorld--A Wolfram Web Resource. Cite error: Invalid
<ref>tag; name "mathematicaWeisstein" defined multiple times with different content
http://en.citizendium.org/wiki/Lambert_W_function
http://en.wikipedia.org/wiki/Lambert_W_function
Keywords
AuZex, Doya function, LambertW.cin, SuZex, Tania function, zex,