Special function
Special function is any mathematical function, supplied with the following:
1. Formal definition, that indicates the way of evaluation of the function. In the most of cases, this refers to a holomorphic function of a single complex variable.
2. Alternative representations of the function, relation of the function to other elementary functions or with other special functions, defined earlier; even if the relation is asymptotic or approximate. [1][2]
3. Properties of the function for the real values of the argument, especially if the function is real–holomorphic: zeros, maxima, minima. Some special values; in particular, value at zero, if it is finite.
4. Asymptotic expansions; for example, that at zero and that at infinity.
5. Numerical implementation, that allows to evaluate the function with several decimal digits. For example, the relatively new special functions tetration to natural base (id est, tet) and the superfactorial (id est, SuFac) are implemented with 14 decimal digits in wide range of values of the argument; this range and the precision are limited, mainly, by the rounding errors and the range of representation of numbers in the complex double variables.
6. Explicit plot of the function for real values of the argument.
7. Complex map of the function; especially if it is holomorphic at least in some part of the complex plane.
8. References to publications, where this function is described or used for some applications, for example, for evaluation of other functions or for formulation of some nontrivial scientific concepts.
Elementary function
Important subset of special functions is set of elementary functions.
Elementary functions appear as
(1) first three ackermann functions, id est, addition, multiplication and exponentialtion, or
(2) their inverse functions, id est, subtraction, division, logarithm and root finding (for example, sort), or
(3) finite combinations of the functions mentioned in (1) or (2) above.
Several elementary functions are qualified as primary elementary functions:
addition and subtraction
sin, arcsin, cos, arccos, tan, arctan,
sinh, arcsinh, cosh, arccosh, tanh, arctanh
The main reason for this classification is, that the primary elementary functions are considered at schools; often, before of define correctly the complex numbers, differentiation, and integration.
sin, arcsin, cos, arccos, tan, arctan are qualified as primary trigonometric functions;
sinh, arcsinh, cosh, arccosh, tanh, arctanh are qualified as primary hyperbolic functions.
Terminology
Some colleagues tend to call "special functions" those that appear at the textbooks. Some textbooks are qualified as authoritet sources, and only functions described there are considered as special.
For the goals of TORI, the definitions of terms authoritet source and scientific fact slightly deviates from those, suggested in schools or wikipedia; accordingly, the term special function may refers to a function, which is not yet included to the widely spread textbook. However, the description of the special function still should have all the 8 properties mentioned in the preamble, and the concept about that function is supposed to satisfy the TORI axioms, even if the rigorous mathematical proof of some statements is not yet available.
Justification
Amount of functions, that can be described by a single researcher, is limited. The choice of the objects of investigation is important. The following reasons to investigate the function and to upgrade it to the status of special function are considered as serious.
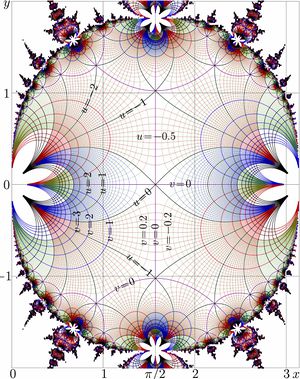
1. Function appears in the physical model, that describes or pretends to describe some physical effect.
2. Function appear in any scientific research, is used in description and/or application of any scientific concept.
3. Function is declared in public to be impossible to built-up or to calculate with sufficient precision in realtime.
4. Function can be used as illustration for some more general principle, some non–trivial scientific concept.
5. The complex map of this function or its explicit plot is beautiful.
Often, the range of primary application of a function is narrow; id est, namely for this application, the function appears inly in small region of the complex plane; often, only for the real values of the argument or even for only a piece of the real axis (for example, for positive values of the argument). This narrow area of application does not justify the restriction of consideration of function in the whole complex plane. This extension may be limited only by the explicit cut line, that limits the range of holomorphism of the function.
For example, the complex map of function AuSin (that is Abel function for sin) seems to be limited by the region where the function shows fast oscillations. This can be considered as justification, why the function is not defined (nor implemented) outside some range. Complex map of function AuSin is shown in figure at right.
In other cases, the holomorphic extension, preferably, to the whole complex plane, should be supplied and implemented. Even if the application of the function for complex argument is not yet suggested, one may expect this application to appear in future. In particular, the trigonometric functions, mentioned above, first were introduced only for real values of the argument; the extension to the complex plane begins, roughly, in 1748 with Leonhard Euler, with the Euler identity
\(\mathrm e^{\mathrm i \pi} +1=0\)
and its more general and more complicated modifications. [3][4].
References
- ↑ For example, is the dollar, ruble and pound are already defined, then formula One pound of rubles is equivalent of one dollar would be suitable in their descriptions as special functions.
- ↑
One friend of mine found:
Let all constants be round;
Let all, \(\pi\) and \(\mathrm e\)
Be equal to three;
And kilogram be 2 lb. - ↑ https://en.wikipedia.org/wiki/Euler%27s_identity
- ↑ http://www.17centurymaths.com/contents/introductiontoanalysisvol1.htm http://www.17centurymaths.com/contents/euler/introductiontoanalysisvolone/ch8vol1.pdf EULER'S INTRODUCTIO IN ANALYSIN INFINITORUM Translated and annotated by Ian Bruce. Ian Bruce. Jan. 16th , 2013 latest revision.
Keywords
AuFac, AuSin, AuTra, Holomorphic function, IRENE, sin, SuFac, SuSin, SuTra, tet,