SuSin
SuSin, or "super sin", is superfunction [1] of the trigonometric function sin; id est, solution SuSin of equations
\((1)~ ~ ~ \mathrm{SuSin}(z\!+\!1)= \sin(\mathrm{SuSin}(z))\)
\((2)~ ~ ~\mathrm{SuSin}(1)=1\)
with specific behaviour at infinity, namely, at large \(|z|\),
\((3) ~ ~ ~ \displaystyle \mathrm{SuSin}(z)= \sqrt{\frac{3}{z}} \left(1 - \frac{3}{10} \frac{\ln(z)}{z}+ O\left(\frac{1}{z}\right) \right)\)
This asymptotic behaviour can be used for the evaluation. [2].
The explicit plot of SuSin is shown at the upper figure; \(y=\mathrm{SuSin}(x)\)
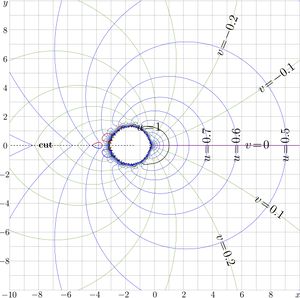
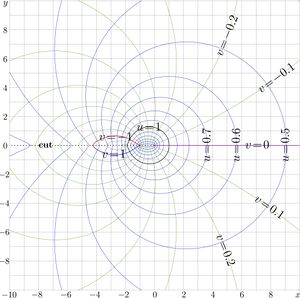
Complex map of \(~f=\mathrm{SuSin}(x\!+\!\mathrm i y)~ ~\) is shown at right with lines \(u\!=\!\Re(f)\!=\!\mathrm {const}\) and lines \(v\!=\!\Im(f)\!=\!\mathrm {const}\), id est,
\((4) ~ ~ ~ u+\mathrm i v= \mathrm{SuSin}(x\!+\!\mathrm i y)\)
Expansion at zero
For small values of the argument, SuSin can be expanded as follows:
\( \displaystyle \mathrm{SuSin}(z) = \frac{\pi}{2}- \sqrt{z} \sum_{m=0}^{M} d_m z^m +O(z^{M+3/2})\)
where \(d\) are real constant. Approximations of the first 6 of them are shown below.
\( d_0 \approx ~~ 0.66058238000675866\)
\( d_1 \approx \! -0.12329860399822383\)
\( d_2 \approx ~~ 0.05094582111507682\)
\( d_3 \approx \! -0.02828892576497096\)
\( d_4 \approx ~~ 0.01839521673418167\)
\( d_5 \approx \! -0.01316131268330939\)
These coefficients are evaluated inverting the expansion of AuSin at \(\pi/2\).
Other properties of SuSin
SuSin can be written as iteration of \(\sin\), id est
\((5)~ ~ ~ \mathrm{SuSin}(z)= \sin^z(\pi/2)\)
As usually, in TORI, the superscript after a name of a function indicates the number of iterations. This notation is borrowed from Quantum mechanics, where \(P^n (\psi)\) means that operaor \(P\) is applied \(n\) times to state \(\psi\), but never means \((P(\psi))^n\). The same notation is used also in articles on iteration of functions [3].
Iterations of function sin, beginning with unity, indicate the set of specific values:
\((6)~ ~ ~ \mathrm{SuSin}(0) = \pi/2 \approx 1.57079632679\)
and SuSin has branch point at zero; the cut line along the negative part of the real axis is marked at the complex map. Then,
\((7)~ ~ ~ \mathrm{SuSin}(0) = 1\)
by definition. Iterating sin, one gets:
\((8)~ ~ ~ \mathrm{SuSin}(1) = \sin(1) \approx 0.8414709848\)
\((9)~ ~ ~ \mathrm{SuSin}(2) = \sin^2(1) = \sin(\sin(1)) \approx 0.74562414166\)
and so on. The use of asymptotic of SuSin allows to evaluate it at large values of the real part of the argument. Then, SuSin at moderate values of argument can be evaluated iterating relation
\((10)~ ~ ~ \mathrm{SuSin}(z)= \sin^{-1}(\mathrm{SuSin}(z\!+\!1)) = \arcsin(\mathrm{SuSin}(z\!+\!1))\)
These iterations are implemented in the generators of figures. However, the implementation of ArcSin function is also necessary.
Evaluation
For the evaluation of SuSin, the asymptotic expansion (3) can be used.
Let \(M\!>\!1\) be positive integer number. Let
\((11)~ ~ ~\displaystyle P_m(L)=\sum_{n=0}^m a_{m,n}L^n\)
\((12)~ ~ ~\displaystyle F_M(z)=\sqrt{\frac{3}{z}} \left( 1-\frac{3\ln(z)}{10~ z}+\sum_{m=2}^M \frac{P_m(\ln(z))}{z^m} \right)\)
In order to construct the solution \(F\) of the transfer equation \(F(z\!+\!1)=\sin(F(z))\), assume, that
\((13) ~ ~ ~ \displaystyle F(z)=F_M(z)+O\left(\frac{\ln(z)}{z}\right)^{M+1}\)
and substitute this asymptotic expansion into the equation. It is convenient to set \(a_{1,0}=0\). Then, the substitution gives the coefficients \(a\) in equation(11). Several first coefficients are shown in the table below: \( \begin{array}{ccccccc} 0 & -\frac{3}{10} & a(1,2) & a(1,3) & a(1,4) & a(1,5) & a(1,6) \\ \frac{79}{700} & -\frac{9}{50} & \frac{27}{200} & a(2,3) & a(2,4) & a(2,5) & a(2,6) \\ \frac{411}{3500} & -\frac{1941}{7000} & \frac{27}{125} & -\frac{27}{400} & a(3,4) & a(3,5) & a(3,6) \\ \frac{1606257}{10780000} & -\frac{7227}{17500} & \frac{1683}{4000} & -\frac{1917}{10000} & \frac{567}{16000} & a(4,5) & a(4,6) \\ \frac{140345627}{700700000} & -\frac{70079931}{107800000} & \frac{566973}{700000} & -\frac{98739}{200000} & \frac{7533}{50000} & -\frac{15309}{800000} & a(5,6) \\ \frac{137678711441}{490490000000} & -\frac{7364523}{7007000} & \frac{305491257}{196000000} & -\frac{4155111}{3500000} & \frac{796311}{1600000} & -\frac{2218347}{20000000} & \frac{168399}{16000000} \end{array} \)
Coefficients \(a\) are calculated with the Mathematica code below
P[m_, L_] := Sum[a[m, n] L^n, {n, 0, m}]
F[z_] = Sqrt[3/z] ( 1 + Sum[P[m, Log[z]]/z^m, {m, 1, M}])
M = 9; a[1, 0] = 0;
F1x = F[1 + 1/x];
Ftx = Sin[F[1/x]];
s[1] = Series[(F1x - Ftx)/Sqrt[x], {x, 0, 2}]
t[1] = Extract[Solve [Coefficient[s[1], x^2] == 0, {a[1, 1]}], 1]
A[1, 1] = ReplaceAll[a[1, 1], t[1]]
su[1] = t[1]
m = 2; s[m] = Simplify[ReplaceAll[Series[(F1x - Ftx)/Sqrt[3 x], {x, 0, m + 1}], su[m - 1]]]
t[m] = Simplify[Coefficient[ReplaceAll[s[m], Log[x] -> L], x^(m + 1)]]
u[m] = Simplify[Collect[t[m], L]]
v[m] = Table[Coefficient[u[m] L, L^(n + 1)] == 0, {n, 0, m}]
w[m] = Table[a[m, n], {n, 0, m}]
ad[m] = Extract[Solve[v[m], w[m]], 1]
su[m] = Join[su[m - 1], ad[m]]
m = 3; s[m] = Simplify[ReplaceAll[Series[(F1x - Ftx)/Sqrt[3 x], {x, 0, m + 1}], su[m - 1]]];
t[m] = Simplify[Coefficient[ReplaceAll[s[m], Log[x] -> L], x^(m + 1)]];
u[m] = Simplify[Collect[t[m], L]];
v[m] = Table[Coefficient[u[m] L, L^(n + 1)] == 0, {n, 0, m}];
w[m] = Table[a[m, n], {n, 0, m}];
ad[m] = Extract[Solve[v[m], w[m]], 1];
su[m] = Join[su[m - 1], ad[m]]
and so on.
For \(M\!=\!8\), the complex map of function \(F_M\) is shown in figure at right. In order to simplify the comparisom with map of SuSin above, the argument is displaced for constant \(x_1\approx 1.43\) defined below. In the range \(|z\!-\!1.5|>2\), expression \(F_8(z\!+\!x_1)\) approximates \(\mathrm{SuTra}(z)\); the complex maps practically coincide at the overlapping.
Define function \(F\) with
\((15) ~ ~ ~ \displaystyle F(z)=\lim_{n \rightarrow \infty} \arcsin^n \Big(~F_M(z\!+\!n)~\Big)\)
Where arcsin\(=\!\sin^{-1}\) is primary elementary function. The integer iterate causes no problems, except the case when the argument becomes real number larger than \(\pi/2\); these values determines the cut line of function SuSin, expressed through \(F\).
Let \(x_1\approx 1.4304553465285 ~\) be solution of equation
\((16) ~ ~ ~ F(1+x_1)=1\)
Then, function SuSin can be expressed as follows:
\((17) ~ ~ ~ \mathrm{SuSin}(z)=F(x_1\!+\!z)\)
The limit in equation \(15\) converges quickly. With \(M\!=\!8\), at \(z\) of order of unity, of order of 14 significant figures can be achieved with \(n\!=\!40\) iterations of function arcsin in the right hand side of (15). This provides the efficient algorithm for evaluation of function SuSin. This algorithm is implemented in C++ in the routine loaded as routine susin.cin. In particular, with this algorithm, all the figures in this article can be generated in real time with the codes supplied.
Approximation of SuSin

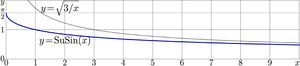
SuSin can be approximated with elementary functions. Approximation of SuSin at large values of the argument can be provided with truncation of its asymptotic expansion above. The leading term of this expansion had been suggested by Kursernas Hemsido in year approximately 2012 [4]. For real argument, this approximation is shown in the explicit plot with thin line. Kursernas Hemsidor denotes this approximation Niklas Carlsson's formula.
Also, in year 2012, Thomas Curtright had suggested the approximation for moderate values of the argument [5]:
\(\mathrm{SuSin}(z) \approx \mathrm{tom}(z)=\exp\Big( \big(1-\sqrt{z}\big) \ln(\pi/2) \Big)\)
This approximation is shown in the explicit plot with dashed line. The deviation of the approximation from the precise evaluation can be seen at the zooming; \(~\mathrm{tom}(x)\!<\!\mathrm{SuSin}(x)~\) at \(~x\!>\!1~\) and at \(~x\!<\!0.3~\), but \(~\mathrm{tom}(x)>\mathrm{SuSin}(x)~\) at \(~0.4\!<\!x\!<\!1~\).
In the same figure, the deviation of function «tom» from SuSin is shown, scaled with factor 10; the thin solid red curve represents \(~y\!=\!10\big(\mathrm{tom}(z)-\mathrm{SuSin}(z)\big)~\).
For \(~|z\!-\!1|<1~\), the approximation \(\mathrm{tom}\) provides at least two significant figures and can be used for plotting of non–integer iterates of sin.
Abel function of sin
The inverse function of \(\mathrm {SuSin}\) is Abel function of sin; let it be called AuSin, \(\mathrm{AuSin}=\mathrm{SuSin}^{-1}\), in such a way that
\((18) ~ ~ ~ \mathrm{SuSin}(\mathrm{AuSin}(z))=z\)
in wide range of values of \(z\).
Function AuSin satisfied the Abel equation
\((19) ~ ~ ~ \mathrm{AuSin}(\sin(z))=\mathrm{AuSin}(z)+1\)
For function AuSin, the asymptotic expansion can be achieved inverting representation (3) of SuSin
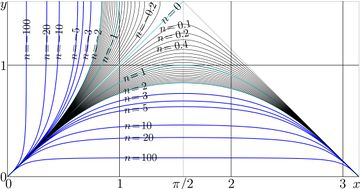
With SuSin and AuSin, the iterates of sin can be expressed as follows:
\( ~ ~ ~ \sin^n(z)=\mathrm{SuSin}(n\!+\!\mathrm{Ausin}(z))\)
In this representation, number \(n\) of iterate has no need to be integer. Iterates of sin are shown in figure at right.
Application of SuSin
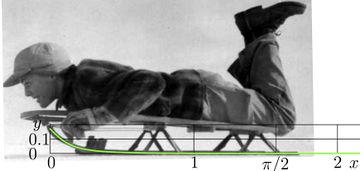
The representation through superfunction and the Abel function can be used to calculate high iterates, avoiding accumulation of the rounding errors at the repeated evaluation of the transfer function. This may have sense, even if the number of iterates is not integer. One example is shown in figure at right. Function \(\sin^{100}\) fits the shape of the main detail of a sled shown in the figure [7]. The shape of the sledge runner from the image by [6] is approximated with function
\(y=\sin^n(\pi/2)-\sin^n(x)\)
with \(n\!=\!100\). The representation through SuSin and the AuSin, id est, \(\sin^n(x)=\mathrm{SuSin}(n+\mathrm{AuSin}(x))\) is used to plot the figure. The deviation is small in compare to the thickness of the sled and that of the curve in the curve.
In general, use of superfunctions and the resulting non-integer iterates greatly extend the arsenal of functions, available for fitting of any physical dependences. One may expect, that use of superfunctions allow to improve the approximation (and extrapolation) of various data. In more specific form (to satisfy the TORI axioms), this expectation is formulated as Conjecture on superfunctions. The figure at right illustrates of that conjecture.
References
- ↑
http://www.springerlink.com/content/qt31671237421111/fulltext.pdf?page=1
http://mizugadro.mydns.jp/PAPERS/2010superfae.pdf D.Kouznetsov, H.Trappmann. Superfunctions and square root of factorial. Moscow University Physics Bulletin, 2010, v.65, No.1, p.6-12. (Russian version: p.8-14) - ↑
http://mizugadro.mydns.jp/PAPERS/2014susinL.pdf
http://mizugadro.mydns.jp/PAPERS/2014susin.pdf D.Kouznetsov. Super sin. Far East Journal of Mathematical Science, v.85, No.2, 2014, pages 219-238. - ↑ http://www.ams.org/journals/bull/1993-29-02/S0273-0979-1993-00432-4/S0273-0979-1993-00432-4.pdf Walter Bergweiler. Iteration of meromorphic functions. Bull. Amer. Math. Soc. 29 (1993), 151-188
- ↑ http://web.abo.fi/fak/mnf/mate/kurser/dynsyst/Iteration%20of%20sin(x).pdf Kursernas Hemsidor. 273027 Introduction to Dynamical Systems 2012. Derivation of Niklas Carlsson;s formula. Cited by the state for December 2013: Let function f(x) be sin(x). We want to evaluate, approximately, the value of the nth iterate of f(x) ... If the formula is correct, it will take 3⋅1010 .. steps to reat 0.00001 from 1. .. fn(x)≈3n‾‾√, x≈1, n lage ... How good is this formula? after 60000 iterations of the value 0.0071 and the discrepancy -4.7s-007 ..
- ↑ http://server.physics.miami.edu/~curtright/Schroeder.html Dr. Thomas Curtright. Continuous iterates continue to be interesting, after 150 years of study. (2012) As a first illustration, we display the continuous iterates of the sine function, sin[t](x). Note that the maximum values at x = π/2 are approximately given by exp[(1-√t) ln(π/2)].
- ↑ 6.0 6.1 http://en.wikipedia.org/wiki/File:Boy_on_snow_sled,_1945.jpg Father of JGKlein. Boy on snow sled, 1945.
- ↑ 7.0 7.1 http://mizugadro.mydns.jp/PAPERS/2014susin.pdf Dmitrii Kouznetsov. Super sin. December 17, 2013. Iterates of function sin are considered. The superfunction SuSin is constructed as holomorphic solution of the transfer equation sin(SuSin(z))=SuSin(z+1). The Abel function AuSin is constructed as solution of the Abel equation AuSin(sin(z))=AuSin(z)+1; in wide range of values z, the relation SuSin(AuSin(z))=z holds. Iteration of sin is expressed with sinˆn(z)=SuSin(n+AuSin(z)), where the number n of iteration has no need to be integer. ..
http://www.proofwiki.org/wiki/Definition:Superfunction
http://en.citizendium.org/wiki/Superfunction
http://en.wikipedia.org/wiki/Superfunction
http://en.citizendium.org/wiki/Sine
http://en.wikipedia.org/wiki/Fixed-point_iteration
http://web.abo.fi/fak/mnf/mate/kurser/dynsyst/Iteration%20of%20sin(x).pdf Kursernas Hemsidor. 273027 Introduction to Dynamical Systems 2012. Derivation of Niklas Carlsson;s formula. Cited by the state for December 2013: Let function f(x) be sin(x). We want to evaluate, approximately, the value of the nth iterate of f(x) ... If the formula is correct, it will take 3⋅1010 .. steps to reat 0.00001 from 1. .. \(f^n(x)\approx \sqrt{\frac{3}{n}}\), \(x\approx 1\), \(n\) lage ... How good is this formula? after 60000 iterations of the value 0.0071 and the discrepancy -4.7s-007 ..
http://server.physics.miami.edu/~curtright/Schroeder.html Dr. Thomas Curtright. Continuous iterates continue to be interesting, after 150 years of study. (2012) As a first illustration, we display the continuous iterates of the sine function, sin[t](x). Note that the maximum values at x = π/2 are approximately given by exp[(1-√t) ln(π/2)].
Keywords
«AuSin», «Iteration», «Superfunction», «Superfunctions», «Sin», «SuSin», «susin.cin», «ausin.cin»,