Difference between revisions of "ArqNem"

From TORI
Jump to navigation Jump to search
 
m (Text replacement - "\$([^\$]+)\$" to "\\(\1\\)")
 
Line 1: Line 1:
−
[[File:Arqnemplot.jpg|400px|thumb|$y\!=\!\mathrm{ArqNem}_{q}(x)$ versus $x$ for various $q$]]
 +
[[File:Arqnemplot.jpg|400px|thumb|\(y\!=\!\mathrm{ArqNem}_{q}(x)\) versus \(x\) for various \(q\)]]
−
[[File:Arqnem00zt.jpg|400px|thumb|$u\!+\!\mathrm i v=\mathrm{ArqNem}_{0}(x\!+\!\mathrm i y)$]]
 +
[[File:Arqnem00zt.jpg|400px|thumb|\(u\!+\!\mathrm i v=\mathrm{ArqNem}_{0}(x\!+\!\mathrm i y)\)]]
−
[[File:Arqnem10zt.jpg|400px|thumb|$u\!+\!\mathrm i v=\mathrm{ArqNem}_{1}(x\!+\!\mathrm i y)$]]
 +
[[File:Arqnem10zt.jpg|400px|thumb|\(u\!+\!\mathrm i v=\mathrm{ArqNem}_{1}(x\!+\!\mathrm i y)\)]]
−
[[File:Arqnem20zt.jpg|400px|thumb|$u\!+\!\mathrm i v=\mathrm{ArqNem}_{2}(x\!+\!\mathrm i y)$]]
 +
[[File:Arqnem20zt.jpg|400px|thumb|\(u\!+\!\mathrm i v=\mathrm{ArqNem}_{2}(x\!+\!\mathrm i y)\)]]
   
 
[[ArqNem]] is one of the [[inverse function]]s of the [[Nemtsov function]] Nem:
  
[[ArqNem]] is one of the [[inverse function]]s of the [[Nemtsov function]] Nem:
   
−
$\mathrm{Nem}(\mathrm{ArqNem}(z))=z$
 +
\(\mathrm{Nem}(\mathrm{ArqNem}(z))=z\)
   
 
where
 
where
   
−
$\mathrm{Nem}(z)=\mathrm{Nem}_{q}(z)=z+z^3+qz^4$
 +
\(\mathrm{Nem}(z)=\mathrm{Nem}_{q}(z)=z+z^3+qz^4\)
   
−
If it is necessary to specify value of parameter $q$, it is indicated as subscript after the name of function Nem or ArqNem.
 +
If it is necessary to specify value of parameter \(q\), it is indicated as subscript after the name of function Nem or ArqNem.
   
−
Explicit plot $y\!=\!\mathrm{ArqNem}_{q}(x)$ versus $x$ for various $q$ is shown in figure at right.
 +
Explicit plot \(y\!=\!\mathrm{ArqNem}_{q}(x)\) versus \(x\) for various \(q\) is shown in figure at right.
   
 
==Complex maps==
  
==Complex maps==
   
−
Complex maps of function $\mathrm{ArqNem}_q(z)$ is shown in figures at right for
+
Complex maps of function \(\mathrm{ArqNem}_q(z)\) is shown in figures at right for
−
$q\!=\!0$,
 +
\(q\!=\!0\),
−
$q\!=\!1$ and
 +
\(q\!=\!1\) and
−
$q\!=\!2$.
 +
\(q\!=\!2\).
   
 
In the complex plane
 
In the complex plane
−
$x\!=\!\Re(z)$,
 +
\(x\!=\!\Re(z)\),
−
$y\!=\!\Im(z)$,
 +
\(y\!=\!\Im(z)\),
 
the function is represented with
 
the function is represented with
−
levels $u=\Re(\mathrm{ArqNem}(z))=\mathrm{const}$ and
+
levels \(u=\Re(\mathrm{ArqNem}(z))=\mathrm{const}\) and
−
levels $v=\Im(\mathrm{ArqNem}(z))=\mathrm{const}$,
 +
levels \(v=\Im(\mathrm{ArqNem}(z))=\mathrm{const}\),
 
id est,
  
id est,
   
−
$u\!+\!\mathrm i v=\mathrm{ArqNem}_q(x\!+\!\mathrm i y)$
 +
\(u\!+\!\mathrm i v=\mathrm{ArqNem}_q(x\!+\!\mathrm i y)\)
   
 
The cut lines are marked with yellow lines. Region
 
The cut lines are marked with yellow lines. Region
−
$-\!1\!<x\!<1$,
+
\(-\!1\!<x\!<1\),
−
$-\!1\!<x\!<1$
 +
\(-\!1\!<x\!<1\)
 
is covered with the maps.
  
is covered with the maps.
−
The grid lines are drawn with interval $0.5$ ;
+
The grid lines are drawn with interval \(0.5\) ;
 
Additional grid lines are drawn through the branch points.
  
Additional grid lines are drawn through the branch points.
   
Line 43: Line 43:
 
In general, equation
 
In general, equation
   
−
$\mathrm {Nem}_q(t)=z$
 +
\(\mathrm {Nem}_q(t)=z\)
   
−
at fixed $q\!\ne\!0$ has 4 solutions.
 +
at fixed \(q\!\ne\!0\) has 4 solutions.
 
Aiming the application in the physical science, the real-holomorphic solutions are of special interest. One of them is ArqNem.
 
Aiming the application in the physical science, the real-holomorphic solutions are of special interest. One of them is ArqNem.
   
 
This solution grows up from zero to infinity along the positive part of the real axis.
  
This solution grows up from zero to infinity along the positive part of the real axis.
   
−
The branch points for all inverse functions of the [[Nemtsov function]] $\mathrm {Nem}_q$ are the same.
 +
The branch points for all inverse functions of the [[Nemtsov function]] \(\mathrm {Nem}_q\) are the same.
−
For positive $q$ one of them is at the negative part of the real axis and goes to $-\infty$ as $q\rightarrow 0$.
 +
For positive \(q\) one of them is at the negative part of the real axis and goes to \(-\infty\) as \(q\rightarrow 0\).
−
One other is expressed with function [[NemBran]] of parameter $q$.
 +
One other is expressed with function [[NemBran]] of parameter \(q\).
−
For positive $q$, another one can be obtained with just linear conjugation.
 +
For positive \(q\), another one can be obtained with just linear conjugation.
−
In the complex maps, there branch points are denoted as $x_0\pm y_0$ and are marked with additional grid lines.
 +
In the complex maps, there branch points are denoted as \(x_0\pm y_0\) and are marked with additional grid lines.
   
 
For ArqNem, all the branch points are connected with cut lines.
  
For ArqNem, all the branch points are connected with cut lines.
−
One of them goes along the negative part of the real axis, id est, from $-\infty$ to zero.
 +
One of them goes along the negative part of the real axis, id est, from \(-\infty\) to zero.
−
Two others are straight lines from zero to $x_0 \pm \mathrm i y_0$.
 +
Two others are straight lines from zero to \(x_0 \pm \mathrm i y_0\).
   
 
In the complex maps, these cuts are marked with straight yellow lines and labeled with symbol '''cut'''.
  
In the complex maps, these cuts are marked with straight yellow lines and labeled with symbol '''cut'''.
Line 66: Line 66:
 
==Implementation==
  
==Implementation==
   
−
For $q>0$, the [[C++]] implementation of function $\mathrm{ArqNem}_q$ is suggested below. Note, that value of parameter $q$ and
 +
For \(q>0\), the [[C++]] implementation of function \(\mathrm{ArqNem}_q\) is suggested below. Note, that value of parameter \(q\) and
 
values of the real and imaginary parts of the branch point should be stored in global <double> variables Q, tr, ti, respectively.
  
values of the real and imaginary parts of the branch point should be stored in global <double> variables Q, tr, ti, respectively.
 
At given Q, values of tr and ti can be evlauated through routine [[nembran.cin]].
  
At given Q, values of tr and ti can be evlauated through routine [[nembran.cin]].
 
Four different functions are used dependently on the argument; in order to choose the appropriate algorithm, tr and ti are necessary.
  
Four different functions are used dependently on the argument; in order to choose the appropriate algorithm, tr and ti are necessary.
   
−
For positive values of argument $z$, and also, for $z$ in some vicinity of the real axis, routine arnemR(z) can be used to evaluate ArqNem.
 +
For positive values of argument \(z\), and also, for \(z\) in some vicinity of the real axis, routine arnemR(z) can be used to evaluate ArqNem.
   
−
The algorithm works for $\mathrm{ArqNem}_q$ at $q\!>\!10^{-7}$. In order to plot map for $q\!=\!0$, the approximation with $q\!=\!10^{-6}$ is used;
 +
The algorithm works for \(\mathrm{ArqNem}_q\) at \(q\!>\!10^{-7}\). In order to plot map for \(q\!=\!0\), the approximation with \(q\!=\!10^{-6}\) is used;
−
it still allows the zoom-in with scaling factor of order of 100, and deviation from the case $q\!=\!0$ is not yet seen.
 +
it still allows the zoom-in with scaling factor of order of 100, and deviation from the case \(q\!=\!0\) is not yet seen.
   
 
The code [[Arqnem.cin]] is copipasted below:
  
The code [[Arqnem.cin]] is copipasted below:
Line 146: Line 146:
 
==Application==
  
==Application==
   
−
The [[Nemtsov function]] $\mathrm{Nem}_q$ is considered as a [[transfer function]] in the book [[Superfunctions]] as an example of the [[exotic iterate]].
 +
The [[Nemtsov function]] \(\mathrm{Nem}_q\) is considered as a [[transfer function]] in the book [[Superfunctions]] as an example of the [[exotic iterate]].
   
 
Fore the iterates of the [[Nemtsov function]], the corresponding [[superfunction]] [[SuNem]] and the corresponding [[Abel function]] [[AuNem]] are necessary.
  
Fore the iterates of the [[Nemtsov function]], the corresponding [[superfunction]] [[SuNem]] and the corresponding [[Abel function]] [[AuNem]] are necessary.
Line 153: Line 153:
 
In certain range of the argument, for evaluation of the Abel function, other inverse function can be used. However, for the numerical analysis of the Abel function, the algorithm for the whole complex plane is necessary. For this analysis, function [[ArqNem]] is constructed and implemented.
  
In certain range of the argument, for evaluation of the Abel function, other inverse function can be used. However, for the numerical analysis of the Abel function, the algorithm for the whole complex plane is necessary. For this analysis, function [[ArqNem]] is constructed and implemented.
   
−
The scientific interest about [[Nemtsov function]] and its inverse [[ArqNem]] refers to the attempt to suggest a holomorphic function such that its non–integer iterate cannot be constructed as a holomorphic function. While the pretentious hypothesis holds, that for any holomorphic function $T$, the holomorphic [[superfunction]] $F$ and the corresponding [[abel function]] $G$ can be constructed, and then, the $n$th iterate of function $T$ can be defined with
 +
The scientific interest about [[Nemtsov function]] and its inverse [[ArqNem]] refers to the attempt to suggest a holomorphic function such that its non–integer iterate cannot be constructed as a holomorphic function. While the pretentious hypothesis holds, that for any holomorphic function \(T\), the holomorphic [[superfunction]] \(F\) and the corresponding [[abel function]] \(G\) can be constructed, and then, the \(n\)th iterate of function \(T\) can be defined with
   
−
$T^n(z)=F(n+G(z))$
 +
\(T^n(z)=F(n+G(z))\)
   
−
In this case, the number $n$ of iterate has no need to be integer.
 +
In this case, the number \(n\) of iterate has no need to be integer.
   
 
==References==
  
==References==

Latest revision as of 18:46, 30 July 2019

\(y\!=\!\mathrm{ArqNem}_{q}(x)\) versus \(x\) for various \(q\)
\(u\!+\!\mathrm i v=\mathrm{ArqNem}_{0}(x\!+\!\mathrm i y)\)
\(u\!+\!\mathrm i v=\mathrm{ArqNem}_{1}(x\!+\!\mathrm i y)\)
\(u\!+\!\mathrm i v=\mathrm{ArqNem}_{2}(x\!+\!\mathrm i y)\)

ArqNem is one of the inverse functions of the Nemtsov function Nem:

\(\mathrm{Nem}(\mathrm{ArqNem}(z))=z\)

where

\(\mathrm{Nem}(z)=\mathrm{Nem}_{q}(z)=z+z^3+qz^4\)

If it is necessary to specify value of parameter \(q\), it is indicated as subscript after the name of function Nem or ArqNem.

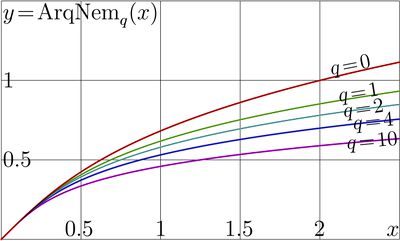
Explicit plot \(y\!=\!\mathrm{ArqNem}_{q}(x)\) versus \(x\) for various \(q\) is shown in figure at right.

Complex maps

Complex maps of function \(\mathrm{ArqNem}_q(z)\) is shown in figures at right for \(q\!=\!0\), \(q\!=\!1\) and \(q\!=\!2\).

In the complex plane \(x\!=\!\Re(z)\), \(y\!=\!\Im(z)\), the function is represented with levels \(u=\Re(\mathrm{ArqNem}(z))=\mathrm{const}\) and levels \(v=\Im(\mathrm{ArqNem}(z))=\mathrm{const}\), id est,

\(u\!+\!\mathrm i v=\mathrm{ArqNem}_q(x\!+\!\mathrm i y)\)

The cut lines are marked with yellow lines. Region \(-\!1\!<x\!<1\), \(-\!1\!<x\!<1\) is covered with the maps. The grid lines are drawn with interval \(0.5\) ; Additional grid lines are drawn through the branch points.

Branch points and cut lines

In general, equation

\(\mathrm {Nem}_q(t)=z\)

at fixed \(q\!\ne\!0\) has 4 solutions. Aiming the application in the physical science, the real-holomorphic solutions are of special interest. One of them is ArqNem.

This solution grows up from zero to infinity along the positive part of the real axis.

The branch points for all inverse functions of the Nemtsov function \(\mathrm {Nem}_q\) are the same. For positive \(q\) one of them is at the negative part of the real axis and goes to \(-\infty\) as \(q\rightarrow 0\). One other is expressed with function NemBran of parameter \(q\). For positive \(q\), another one can be obtained with just linear conjugation. In the complex maps, there branch points are denoted as \(x_0\pm y_0\) and are marked with additional grid lines.

For ArqNem, all the branch points are connected with cut lines. One of them goes along the negative part of the real axis, id est, from \(-\infty\) to zero. Two others are straight lines from zero to \(x_0 \pm \mathrm i y_0\).

In the complex maps, these cuts are marked with straight yellow lines and labeled with symbol cut.

Namely this inverse function of the Nemtsov function happen to be suitable for construction of the Abel function AuNem of the Nemtsov function and the corresponding iterates.

Implementation

For \(q>0\), the C++ implementation of function \(\mathrm{ArqNem}_q\) is suggested below. Note, that value of parameter \(q\) and values of the real and imaginary parts of the branch point should be stored in global <double> variables Q, tr, ti, respectively. At given Q, values of tr and ti can be evlauated through routine nembran.cin. Four different functions are used dependently on the argument; in order to choose the appropriate algorithm, tr and ti are necessary.

For positive values of argument \(z\), and also, for \(z\) in some vicinity of the real axis, routine arnemR(z) can be used to evaluate ArqNem.

The algorithm works for \(\mathrm{ArqNem}_q\) at \(q\!>\!10^{-7}\). In order to plot map for \(q\!=\!0\), the approximation with \(q\!=\!10^{-6}\) is used; it still allows the zoom-in with scaling factor of order of 100, and deviation from the case \(q\!=\!0\) is not yet seen.

The code Arqnem.cin is copipasted below:


// DB Q=1.;
/*
z_type nem(z_type z){ return z*(1.+z*z*(1.+z*Q)); }
z_type nem1(z_type z){ return 1.+z*z*(3.+z*(4.*Q)); } // WARNING: Q is global!

#include"nembran.cin"
z_type NemZo=nembra(Q);
z_type ANemZo=nem(NemZo);
DB tr=Re(ANemZo);
DB ti=Im(ANemZo);
*/

z_type arnemU(z_type z){ DB q=Q; DB q2=q*q; DB q3=q2*q;
z_type a=q-z; z_type b=1.+4.*q*z; z_type r=81.*(a*a)+12.*(b*b*b);
z_type R=-I*sqrt(-r);
z_type s=27.*a + 3.*R; z_type S=pow(s,1./3.);
z_type B=(0.26456684199469993*S)/q - (1.2599210498948732*b)/(q*S);
z_type h=0.25/q2 + B;
z_type H=I*sqrt(-h);
z_type g=0.5/q2 - B + (.25+2.*q2)/(q3*H);
z_type G=I*sqrt(-g);
return - 0.25/q - 0.5*H + 0.5*G ;}

z_type arnemD(z_type z){ DB q=Q; DB q2=q*q; DB q3=q2*q;
z_type a=q-z; z_type b=1.+4.*q*z; z_type r=81.*(a*a)+12.*(b*b*b);
z_type R=I*sqrt(-r);
z_type s=27.*a + 3.*R; z_type S=pow(s,1./3.);
z_type B=(0.26456684199469993*S)/q - (1.2599210498948732*b)/(q*S);
z_type h=0.25/q2 + B;
z_type H=-I*sqrt(-h);
z_type g=0.5/q2 - B + (.25+2.*q2)/(q3*H);
z_type G=-I*sqrt(-g);
return - 0.25/q - 0.5*H + 0.5*G ;}

z_type arnemR(z_type z){ DB q=Q; DB q2=q*q; DB q3=q2*q;
z_type a=q-z; z_type b=1.+4.*q*z; z_type r=81.*(a*a)+12.*(b*b*b);
z_type R=sqrt(r); z_type s=27.*a + 3.*R;
z_type S=pow(s,1./3.);
z_type B=(0.26456684199469993*S)/q - (1.2599210498948732*b)/(q*S);
z_type h=0.25/q2 + B;
z_type H=sqrt(h);
z_type g=0.5/q2 - B + (.25+2.*q2)/(q3*H);
z_type G=sqrt(g);
return - 0.25/q - 0.5*H + 0.5*G ;}

z_type arnemL(z_type z){ DB q=Q; DB q2=q*q; DB q3=q2*q;
z_type a=q-z; z_type b=1.+4.*q*z; z_type r=81.*(a*a)+12.*(b*b*b);
z_type R=-sqrt(r);
z_type s=27.*a + 3.*R; z_type S=pow(s,1./3.);
z_type B=(0.26456684199469993*S)/q - (1.2599210498948732*b)/(q*S);
z_type h=0.25/q2 + B;
z_type H=sqrt(h);
z_type g=0.5/q2 - B + (.25+2.*q2)/(q3*H);
z_type G=sqrt(g);
return - 0.25/q - 0.5*H + 0.5*G ;}

z_type arqnem(z_type z){ DB x,y; x=Re(z);y=Im(z);
if( y>ti || (x<0 && y>=0)) return arnemU(z);
//if(y<0) return conj(arnemU(conj(z)));
if(y<-ti || (x<0 && y<=0)) return arnemD(z);
if(x*ti>fabs(y)*tr) return arnemR(z);
return arnemL(z);
}

Application

The Nemtsov function \(\mathrm{Nem}_q\) is considered as a transfer function in the book Superfunctions as an example of the exotic iterate.

Fore the iterates of the Nemtsov function, the corresponding superfunction SuNem and the corresponding Abel function AuNem are necessary. For construction of AuNem, the inverse of Nemtsov function is necessary. It is important, that negative iterates of the Nemtsov function do not bring the argument to the cut line; and namely ArqNem provides this. In certain range of the argument, for evaluation of the Abel function, other inverse function can be used. However, for the numerical analysis of the Abel function, the algorithm for the whole complex plane is necessary. For this analysis, function ArqNem is constructed and implemented.

The scientific interest about Nemtsov function and its inverse ArqNem refers to the attempt to suggest a holomorphic function such that its non–integer iterate cannot be constructed as a holomorphic function. While the pretentious hypothesis holds, that for any holomorphic function \(T\), the holomorphic superfunction \(F\) and the corresponding abel function \(G\) can be constructed, and then, the \(n\)th iterate of function \(T\) can be defined with

\(T^n(z)=F(n+G(z))\)

In this case, the number \(n\) of iterate has no need to be integer.

References


Keywords

ArcNme, ArkNem, ArqNem, AuNem, Book, Inverse function, Nemtsov function, Superfunctions

Retrieved from "https://mizugadro.mydns.jp/t/index.php?title=ArqNem&oldid=28360"