Difference between revisions of "ArcSin"
m (Text replacement - "\$([^\$]+)\$" to "\\(\1\\)") |
|||
| (One intermediate revision by one other user not shown) | |||
| Line 1: | Line 1: | ||
| − | [[File:AsimapT.png|400px|right|thumb|[[complex map]] of |
+ | [[File:AsimapT.png|400px|right|thumb|[[complex map]] of \(u\!+\!\mathrm i v\!=\!\arcsin(x\!+\!\mathrm i y)\)]] |
'''ArcSin''', or '''asign''', or '''arcsin''' is [[holomorphic function]], inverse of [[sin]]; |
'''ArcSin''', or '''asign''', or '''arcsin''' is [[holomorphic function]], inverse of [[sin]]; |
||
| − | : |
+ | : \(\displaystyle \sin(z) = \frac{\exp(\mathrm i z)- \exp(-\mathrm i z)}{2~ \mathrm i}\) |
| − | + | \(f=\arcsin(z)\) is holomorphic solution \(f\) of equation |
|
| − | : |
+ | : \( \sin(f)=z\) |
| − | such that |
+ | such that \(\arcsin(0)\!=\!0\). |
| + | |||
| + | ==Representation through logarithm== |
||
| + | |||
| ⚫ | |||
| + | |||
| + | \( \arcsin(z)= -\mathrm i \ln\Big( \mathrm i z + \sqrt{1-z^2} \big)\) |
||
| + | |||
| + | Note that expression |
||
| + | |||
| + | \( \arcsin(z)= \mathrm i \ln\Big( -\mathrm i z + \sqrt{1-z^2} \big)\) |
||
| + | |||
| + | is supposed to be also valid and to reproduce the same cut lines. |
||
| ⚫ | |||
==Range of holomorphism== |
==Range of holomorphism== |
||
| − | + | \(\arcsin(z)\) is holomorphic in the whole complex plane except the halflines \(z\!\le\! -1\) and \(z\!\ge\! 1\). |
|
| − | Complex map or |
+ | Complex map or \(f=\arcsin(x+\mathrm i y)\) is shown in figure at right in the \(x\), \(y\) plane with |
| − | levels |
+ | levels \(u=\Re(f)=\mathrm{const}\) and |
| − | levels |
+ | levels \(v=\Im(f)=\mathrm{const}\). |
Thick lines correspond to the Integer values. |
Thick lines correspond to the Integer values. |
||
The cut lines are shown with dashed lines. |
The cut lines are shown with dashed lines. |
||
| − | In vicinity of the cut lines, the real part of ArcSin approach values |
+ | In vicinity of the cut lines, the real part of ArcSin approach values \(\pm \pi/2\). |
==Symmetry== |
==Symmetry== |
||
ArcSin is [[even function]]: |
ArcSin is [[even function]]: |
||
| − | + | \(: \arcsin(-z)=-\arcsin(z)\) |
|
==Real values== |
==Real values== |
||
[[File:AsinplotT.png|right|300px]] |
[[File:AsinplotT.png|right|300px]] |
||
| − | While |
+ | While \(-1\le x\le 1\), id est, along the real axis, \(\arcsin(x)\) has real values. The graphic is plotted in figure at right. |
In particular, |
In particular, |
||
| − | : |
+ | :\( \displaystyle \arcsin(0)=0\) |
| − | : |
+ | :\( \displaystyle \arcsin\left(\frac{1}{2}\right)=\frac{\pi}{6}\) |
| − | : |
+ | :\( \displaystyle \arcsin\left(\frac{1}{\sqrt{2}}\right)=\frac{\pi}{4}\) |
| − | : |
+ | :\( \displaystyle \arcsin\left(\frac{\sqrt{3}}{2}\right)=\frac{\pi}{3}\) |
| − | : |
+ | :\( \displaystyle \arcsin\left(1\right)=\frac{\pi}{2}\) |
==Numerical Implementation of ArcSin== |
==Numerical Implementation of ArcSin== |
||
| Line 49: | Line 60: | ||
else {return M_PI/2.+I*log( z - sqrt(z*z-1.) );} } |
else {return M_PI/2.+I*log( z - sqrt(z*z-1.) );} } |
||
| − | where I denotes the imaginary unity; Re and Im denote the real and imaginary parts; M_PI denotes |
+ | where I denotes the imaginary unity; Re and Im denote the real and imaginary parts; M_PI denotes \(\pi\). |
Fortunately, in the [[C++]] compilers, function [[log]] is already implemented for [[complex double]] argument. |
Fortunately, in the [[C++]] compilers, function [[log]] is already implemented for [[complex double]] argument. |
||
| Line 61: | Line 72: | ||
==Integral representaitons== |
==Integral representaitons== |
||
| − | : |
+ | : \( \displaystyle \!\!\!\!\!\!\!\!\! |
| − | \arcsin(z)=\int_0^z \frac{\mathrm d t}{\sqrt{1-t^2}} |
+ | \arcsin(z)=\int_0^z \frac{\mathrm d t}{\sqrt{1-t^2}}\) |
| − | The appropriate contour of integration may go straight from zero to |
+ | The appropriate contour of integration may go straight from zero to \(z\). |
==Relations to other functions== |
==Relations to other functions== |
||
| − | + | \( \arcsin(z)= - \mathrm i ~\mathrm{arcsinh}( \mathrm i z)\) |
|
where arcsinh=[[ArcSinh]] is inverse function of [[Sinh]]; |
where arcsinh=[[ArcSinh]] is inverse function of [[Sinh]]; |
||
| − | : |
+ | :\( \displaystyle |
| − | \sinh(z)=\frac{\exp(z)+\exp(-z)}{2} |
+ | \sinh(z)=\frac{\exp(z)+\exp(-z)}{2}\) |
[[ArcSinh]] also can be expressed through ArcSin, |
[[ArcSinh]] also can be expressed through ArcSin, |
||
| − | : |
+ | :\( \mathrm{arcsinh}(z)= \mathrm i ~ \arcsin( \mathrm i z)\) |
Also, ArcSin can be expressed through function arccos=[[ArcCos]]: |
Also, ArcSin can be expressed through function arccos=[[ArcCos]]: |
||
| − | : |
+ | : \( \displaystyle |
| − | \arcsin(z) = \frac{\pi}{2} - \arccos(z) |
+ | \arcsin(z) = \frac{\pi}{2} - \arccos(z)\) |
and correspondently, |
and correspondently, |
||
| − | : |
+ | : \( \displaystyle |
| − | \arccos(z) = \frac{\pi}{2} - \arcsin(z) |
+ | \arccos(z) = \frac{\pi}{2} - \arcsin(z)\) |
| + | |||
| ⚫ | |||
| + | The question of implementation arises because some compilers do not recognise asin of complex double argument. |
||
| ⚫ | |||
===Expansion at zero=== |
===Expansion at zero=== |
||
Often, the expansions of Sin and ArcSin at small values of argument are used; |
Often, the expansions of Sin and ArcSin at small values of argument are used; |
||
| − | : |
+ | : \( \displaystyle \!\!\!\!\!\!\!\!\! |
\sin(z)=z |
\sin(z)=z |
||
-\frac{z^3}{3!} |
-\frac{z^3}{3!} |
||
+\frac{z^5}{5!} |
+\frac{z^5}{5!} |
||
| − | -\frac{z^7}{7!} +... |
+ | -\frac{z^7}{7!} +... \) |
| − | : |
+ | : \( \displaystyle \!\!\!\!\!\!\!\!\! |
\arcsin(z)=z |
\arcsin(z)=z |
||
+\frac{z^3}{3!} |
+\frac{z^3}{3!} |
||
+\frac{3z^5}{40} |
+\frac{3z^5}{40} |
||
| − | +\frac{5z^7}{112} +... |
+ | +\frac{5z^7}{112} +... \) |
[[Mathematica]] allows to evaluate many terms of this expantion: |
[[Mathematica]] allows to evaluate many terms of this expantion: |
||
| − | : |
+ | :\( \displaystyle \!\!\!\!\!\!\!\!\! |
\arcsin(z) = z+0.166666666666667 |
\arcsin(z) = z+0.166666666666667 |
||
| − | z^3 |
+ | z^3\) \(+0.0750000000000000 |
| − | z^5 |
+ | z^5\) \(+0.0446428571428571 |
| − | z^7 |
+ | z^7\) \(+0.0303819444444444 |
| − | z^9 |
+ | z^9\) \(+0.0223721590909091 |
| − | z^{11} |
+ | z^{11}\) \(+0.0173527644230769 |
| − | z^{13} |
+ | z^{13}\) \(+0.0139648437500000 |
| − | z^{15} |
+ | z^{15}\) \(+0.0115518008961397 |
| − | z^{17} |
+ | z^{17}\) \(+0.00976160952919408 |
| − | z^{19} |
+ | z^{19}\) \(+0.00839033580961682 |
| − | z^{21} |
+ | z^{21}\) \(+0.00731252587359885 |
| − | z^{23} |
+ | z^{23}\) \(+0.00644721031188965 |
| − | z^{25} |
+ | z^{25}\) \(+.. \) |
| + | |||
| + | Table of coefficients of this expansion: |
||
| + | |||
| + | {1.000000000000000, 0.1666666666666667, 0.07500000000000000, |
||
| + | 0.04464285714285714, 0.03038194444444444, 0.02237215909090909, |
||
| + | 0.01735276442307692, 0.01396484375000000, 0.01155180089613971, |
||
| + | 0.009761609529194079, 0.008390335809616815, 0.007312525873598845, |
||
| + | 0.006447210311889648, 0.005740037670841923, 0.005153309682319904, |
||
| + | 0.004660143486915096, 0.004240907093679363, 0.003880964558837669, |
||
| + | 0.003569205393825935, 0.003297059503473485, 0.003057821649258031, |
||
| + | 0.002846178401108942, 0.002657870638207290, 0.002489448678246883, |
||
| + | 0.002338091892111975, 0.002201473973710138, 0.002077661032518167, |
||
| + | 0.001965033616277284, 0.001862226406403127, 0.001768081120515418, |
||
| + | 0.001681609393583107, 0.001601963275351444, 0.001528411596122568, |
||
| + | 0.001460320894079115, 0.001397139917630253, 0.001338386951275178, |
||
| + | 0.001283639387629029, 0.001232525098500017, 0.001184715256162439, |
||
| + | 0.001139918330702224, 0.001097875046591447}; |
||
===Expansion in vicinity of the branchpoints=== |
===Expansion in vicinity of the branchpoints=== |
||
Extremums of function Sin correspond to branch points of ArcSin. The expansions can be written as follows: |
Extremums of function Sin correspond to branch points of ArcSin. The expansions can be written as follows: |
||
| − | : |
+ | : \( \displaystyle \!\!\!\!\!\!\!\!\! |
| − | \sin\left( - \frac{\pi}{2}+t\right) = -1+ \frac{t^2}{2}-\frac{t^4}{24}+\frac{t^6}{720}-\frac{t^8}{40320}+.. |
+ | \sin\left( - \frac{\pi}{2}+t\right) = -1+ \frac{t^2}{2}-\frac{t^4}{24}+\frac{t^6}{720}-\frac{t^8}{40320}+..\) |
| − | : |
+ | : \( \displaystyle \!\!\!\!\!\!\!\!\! |
\arcsin(-1+t) = |
\arcsin(-1+t) = |
||
-\frac{\pi}{2}+\sqrt{2\,t} |
-\frac{\pi}{2}+\sqrt{2\,t} |
||
+\frac{t^{3/2}}{6\sqrt{2}}+\frac{ 5~ t^{5/2}}{80 \sqrt{2}}+ .. |
+\frac{t^{3/2}}{6\sqrt{2}}+\frac{ 5~ t^{5/2}}{80 \sqrt{2}}+ .. |
||
| + | \) |
||
| − | $ |
||
[[Mathematica]] allows to evaluate many of terms of this expansion; |
[[Mathematica]] allows to evaluate many of terms of this expansion; |
||
| − | : |
+ | : \( \displaystyle \!\!\!\!\!\!\!\!\! |
| − | \arcsin(-1+t) =- 1.5707963267948966 |
+ | \arcsin(-1+t) =- 1.5707963267948966 \) \(+ \sqrt{t} ~ \Big(\) \( 1.4142135623730950 \) \( |
+0.117851130 19775792 |
+0.117851130 19775792 |
||
| − | t |
+ | t\) \( +0.026516504294495532 |
| − | t^2 |
+ | t^2\) \(+0.0078918167543141465 |
| − | t^3 |
+ | t^3\) \(+0.0026854098677874526 |
| − | t^4 |
+ | t^4\) \(+0.00098871908768538028 |
| − | t^5 |
+ | t^5\) \(+0.00038344554362157376 |
| − | t^6 |
+ | t^6\) \(+0.00015429118302868087 |
| − | t^7 |
+ | t^7\) \(+0.000063815287098259552 |
| − | t^8 |
+ | t^8\) \(+0.000026962891771048261 |
| − | t^9 |
+ | t^9\) \(+0.000011587623725414788 |
| − | t^{10} |
+ | t^{10}\) \( |
| − | +0.0000050495474929920175 t^{11} |
+ | +0.0000050495474929920175 t^{11} \) \( |
+0.0000022260088531606476 t^{12} |
+0.0000022260088531606476 t^{12} |
||
+... |
+... |
||
| − | \Big) |
+ | \Big)\) |
Similar expansion of ArcSin can be written at another branch point: |
Similar expansion of ArcSin can be written at another branch point: |
||
| − | : |
+ | : \(\arcsin(1-t) =-\arcsin(-1+t) \) |
| − | The expansions above allow to evaluate ArcSin at least in vicinity of the segment |
+ | The expansions above allow to evaluate ArcSin at least in vicinity of the segment \([-1,1]\); the precision of evaluation |
| − | + | \(s_0\approx \arcsin(z)\) can be improved with the iteration |
|
| − | : |
+ | :\( \displaystyle |
s_{n+1}=s_n+\frac{z-\sin(s_n)}{\sin'(s_n)}=s_n+\frac{z-\sin(s_n)}{\cos(s_n)} |
s_{n+1}=s_n+\frac{z-\sin(s_n)}{\sin'(s_n)}=s_n+\frac{z-\sin(s_n)}{\cos(s_n)} |
||
| + | \) |
||
| − | $ |
||
| + | |||
| + | ==Numeric implementation== |
||
| + | |||
| + | Unfortunately, in many versions of [[C++]], function [[asin]] is implemented only for real values of the argument. |
||
| + | As [[TORI]] are declared to be tools, the implementation it highly desirable. This implementation can be based on the expansions above. |
||
| + | |||
| + | In vicinity of the branch point, the approximation can be written as follows: |
||
| + | |||
| + | \(\displaystyle \arcsin(1-2x^2)=\frac{\pi}{2} - x \sum_{m=0}^M c_m (x^2)^m\) |
||
| + | |||
| + | For some positive integer \(M\). The first 21 coefficients \(c_0 .. c_{20}\) of this expansion are the in the table below: |
||
| + | |||
| + | <nowiki> |
||
| + | {2, 1/3, 3/20, 5/56, 35/576, 63/1408, 231/6656, 143/5120, |
||
| + | 6435/278528, 12155/622592, 46189/2752512, 88179/6029312, |
||
| + | 676039/52428800, 1300075/113246208, 5014575/486539264, |
||
| + | 9694845/1040187392, 100180065/11811160064, 116680311/15032385536, |
||
| + | 2268783825/317827579904, 1472719325/223338299392, |
||
| + | 34461632205/5634997092352} |
||
| + | </nowiki> |
||
| + | |||
| + | For the complex double implementation, the approximation of the table above can be used: |
||
| + | |||
| + | {2.000000000000000, 0.3333333333333333, 0.1500000000000000, |
||
| + | 0.08928571428571429, 0.06076388888888889, 0.04474431818181818, |
||
| + | 0.03470552884615385, 0.02792968750000000, 0.02310360179227941, |
||
| + | 0.01952321905838816, 0.01678067161923363, 0.01462505174719769, |
||
| + | 0.01289442062377930, 0.01148007534168385, 0.01030661936463981, |
||
| + | 0.009320286973830192, 0.008481814187358726, 0.007761929117675338, |
||
| + | 0.007138410787651869, 0.006594119006946969, 0.006115643298516061, |
||
| + | 0.005692356802217884, 0.005315741276414580, 0.004978897356493767, |
||
| + | 0.004676183784223950, 0.004402947947420276, 0.004155322065036335, |
||
| + | 0.003930067232554567, 0.003724452812806255, 0.003536162241030836, |
||
| + | 0.003363218787166214, 0.003203926550702888, 0.003056823192245135, |
||
| + | 0.002920641788158231, 0.002794279835260507, 0.002676773902550357, |
||
| + | 0.002567278775258057, 0.002465050197000034, 0.002369430512324879, |
||
| + | 0.002279836661404447, 0.002195750093182894} |
||
==Keywords== |
==Keywords== |
||
Latest revision as of 18:48, 30 July 2019

ArcSin, or asign, or arcsin is holomorphic function, inverse of sin;
- \(\displaystyle \sin(z) = \frac{\exp(\mathrm i z)- \exp(-\mathrm i z)}{2~ \mathrm i}\)
\(f=\arcsin(z)\) is holomorphic solution \(f\) of equation
- \( \sin(f)=z\)
such that \(\arcsin(0)\!=\!0\).
Representation through logarithm
ArcSin is considered as elementary function, more specifically Inverse trigonometric function. It can be expressed also through logarithm:
\( \arcsin(z)= -\mathrm i \ln\Big( \mathrm i z + \sqrt{1-z^2} \big)\)
Note that expression
\( \arcsin(z)= \mathrm i \ln\Big( -\mathrm i z + \sqrt{1-z^2} \big)\)
is supposed to be also valid and to reproduce the same cut lines.
Range of holomorphism
\(\arcsin(z)\) is holomorphic in the whole complex plane except the halflines \(z\!\le\! -1\) and \(z\!\ge\! 1\).
Complex map or \(f=\arcsin(x+\mathrm i y)\) is shown in figure at right in the \(x\), \(y\) plane with levels \(u=\Re(f)=\mathrm{const}\) and levels \(v=\Im(f)=\mathrm{const}\). Thick lines correspond to the Integer values. The cut lines are shown with dashed lines. In vicinity of the cut lines, the real part of ArcSin approach values \(\pm \pi/2\).
Symmetry
ArcSin is even function: \(: \arcsin(-z)=-\arcsin(z)\)
Real values
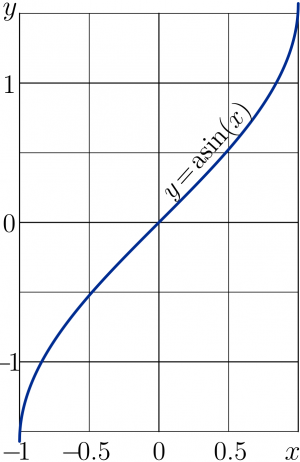
While \(-1\le x\le 1\), id est, along the real axis, \(\arcsin(x)\) has real values. The graphic is plotted in figure at right.
In particular,
- \( \displaystyle \arcsin(0)=0\)
- \( \displaystyle \arcsin\left(\frac{1}{2}\right)=\frac{\pi}{6}\)
- \( \displaystyle \arcsin\left(\frac{1}{\sqrt{2}}\right)=\frac{\pi}{4}\)
- \( \displaystyle \arcsin\left(\frac{\sqrt{3}}{2}\right)=\frac{\pi}{3}\)
- \( \displaystyle \arcsin\left(1\right)=\frac{\pi}{2}\)
Numerical Implementation of ArcSin
In some programing languages, acos is implemented only for real argument. However, it can be expressed through the log function as follows:
complex double asin(complex double z){
if(Im(z)<0){if(Re(z)>=0){return M_PI/2.-I*log( z + sqrt(z*z-1.) );}
else{return M_PI/2.-I*log( z - sqrt(z*z-1.) );}}
if(Re(z)>=0){return M_PI/2.+I*log( z + sqrt(z*z-1.) );}
else {return M_PI/2.+I*log( z - sqrt(z*z-1.) );} }
where I denotes the imaginary unity; Re and Im denote the real and imaginary parts; M_PI denotes \(\pi\).
Fortunately, in the C++ compilers, function log is already implemented for complex double argument.
This implementation above used to plot the complex map of ArcSin at the top figure. In particular, the same representation can be used for real values of the argument; the explicit plot of ArcSin is generated with the same representation. (Click the figure to see the code used for its generation.) However, the last graphic could be generated also with the internal C++ function asin of real argument, as well as with flipping of plot of function sin.
Integral representaitons
- \( \displaystyle \!\!\!\!\!\!\!\!\! \arcsin(z)=\int_0^z \frac{\mathrm d t}{\sqrt{1-t^2}}\)
The appropriate contour of integration may go straight from zero to \(z\).
Relations to other functions
\( \arcsin(z)= - \mathrm i ~\mathrm{arcsinh}( \mathrm i z)\)
where arcsinh=ArcSinh is inverse function of Sinh;
- \( \displaystyle \sinh(z)=\frac{\exp(z)+\exp(-z)}{2}\)
ArcSinh also can be expressed through ArcSin,
- \( \mathrm{arcsinh}(z)= \mathrm i ~ \arcsin( \mathrm i z)\)
Also, ArcSin can be expressed through function arccos=ArcCos:
- \( \displaystyle \arcsin(z) = \frac{\pi}{2} - \arccos(z)\)
and correspondently,
- \( \displaystyle \arccos(z) = \frac{\pi}{2} - \arcsin(z)\)
Expansions and implementations
The question of implementation arises because some compilers do not recognise asin of complex double argument.
Expansion at zero
Often, the expansions of Sin and ArcSin at small values of argument are used;
- \( \displaystyle \!\!\!\!\!\!\!\!\! \sin(z)=z -\frac{z^3}{3!} +\frac{z^5}{5!} -\frac{z^7}{7!} +... \)
- \( \displaystyle \!\!\!\!\!\!\!\!\! \arcsin(z)=z +\frac{z^3}{3!} +\frac{3z^5}{40} +\frac{5z^7}{112} +... \)
Mathematica allows to evaluate many terms of this expantion:
- \( \displaystyle \!\!\!\!\!\!\!\!\! \arcsin(z) = z+0.166666666666667 z^3\) \(+0.0750000000000000 z^5\) \(+0.0446428571428571 z^7\) \(+0.0303819444444444 z^9\) \(+0.0223721590909091 z^{11}\) \(+0.0173527644230769 z^{13}\) \(+0.0139648437500000 z^{15}\) \(+0.0115518008961397 z^{17}\) \(+0.00976160952919408 z^{19}\) \(+0.00839033580961682 z^{21}\) \(+0.00731252587359885 z^{23}\) \(+0.00644721031188965 z^{25}\) \(+.. \)
Table of coefficients of this expansion:
{1.000000000000000, 0.1666666666666667, 0.07500000000000000, 0.04464285714285714, 0.03038194444444444, 0.02237215909090909, 0.01735276442307692, 0.01396484375000000, 0.01155180089613971, 0.009761609529194079, 0.008390335809616815, 0.007312525873598845, 0.006447210311889648, 0.005740037670841923, 0.005153309682319904, 0.004660143486915096, 0.004240907093679363, 0.003880964558837669, 0.003569205393825935, 0.003297059503473485, 0.003057821649258031, 0.002846178401108942, 0.002657870638207290, 0.002489448678246883, 0.002338091892111975, 0.002201473973710138, 0.002077661032518167, 0.001965033616277284, 0.001862226406403127, 0.001768081120515418, 0.001681609393583107, 0.001601963275351444, 0.001528411596122568, 0.001460320894079115, 0.001397139917630253, 0.001338386951275178, 0.001283639387629029, 0.001232525098500017, 0.001184715256162439, 0.001139918330702224, 0.001097875046591447};
Expansion in vicinity of the branchpoints
Extremums of function Sin correspond to branch points of ArcSin. The expansions can be written as follows:
- \( \displaystyle \!\!\!\!\!\!\!\!\! \sin\left( - \frac{\pi}{2}+t\right) = -1+ \frac{t^2}{2}-\frac{t^4}{24}+\frac{t^6}{720}-\frac{t^8}{40320}+..\)
- \( \displaystyle \!\!\!\!\!\!\!\!\! \arcsin(-1+t) = -\frac{\pi}{2}+\sqrt{2\,t} +\frac{t^{3/2}}{6\sqrt{2}}+\frac{ 5~ t^{5/2}}{80 \sqrt{2}}+ .. \)
Mathematica allows to evaluate many of terms of this expansion;
- \( \displaystyle \!\!\!\!\!\!\!\!\! \arcsin(-1+t) =- 1.5707963267948966 \) \(+ \sqrt{t} ~ \Big(\) \( 1.4142135623730950 \) \( +0.117851130 19775792 t\) \( +0.026516504294495532 t^2\) \(+0.0078918167543141465 t^3\) \(+0.0026854098677874526 t^4\) \(+0.00098871908768538028 t^5\) \(+0.00038344554362157376 t^6\) \(+0.00015429118302868087 t^7\) \(+0.000063815287098259552 t^8\) \(+0.000026962891771048261 t^9\) \(+0.000011587623725414788 t^{10}\) \( +0.0000050495474929920175 t^{11} \) \( +0.0000022260088531606476 t^{12} +... \Big)\)
Similar expansion of ArcSin can be written at another branch point:
- \(\arcsin(1-t) =-\arcsin(-1+t) \)
The expansions above allow to evaluate ArcSin at least in vicinity of the segment \([-1,1]\); the precision of evaluation \(s_0\approx \arcsin(z)\) can be improved with the iteration
- \( \displaystyle s_{n+1}=s_n+\frac{z-\sin(s_n)}{\sin'(s_n)}=s_n+\frac{z-\sin(s_n)}{\cos(s_n)} \)
Numeric implementation
Unfortunately, in many versions of C++, function asin is implemented only for real values of the argument. As TORI are declared to be tools, the implementation it highly desirable. This implementation can be based on the expansions above.
In vicinity of the branch point, the approximation can be written as follows:
\(\displaystyle \arcsin(1-2x^2)=\frac{\pi}{2} - x \sum_{m=0}^M c_m (x^2)^m\)
For some positive integer \(M\). The first 21 coefficients \(c_0 .. c_{20}\) of this expansion are the in the table below:
{2, 1/3, 3/20, 5/56, 35/576, 63/1408, 231/6656, 143/5120, 6435/278528, 12155/622592, 46189/2752512, 88179/6029312, 676039/52428800, 1300075/113246208, 5014575/486539264, 9694845/1040187392, 100180065/11811160064, 116680311/15032385536, 2268783825/317827579904, 1472719325/223338299392, 34461632205/5634997092352}
For the complex double implementation, the approximation of the table above can be used:
{2.000000000000000, 0.3333333333333333, 0.1500000000000000, 0.08928571428571429, 0.06076388888888889, 0.04474431818181818, 0.03470552884615385, 0.02792968750000000, 0.02310360179227941, 0.01952321905838816, 0.01678067161923363, 0.01462505174719769, 0.01289442062377930, 0.01148007534168385, 0.01030661936463981, 0.009320286973830192, 0.008481814187358726, 0.007761929117675338, 0.007138410787651869, 0.006594119006946969, 0.006115643298516061, 0.005692356802217884, 0.005315741276414580, 0.004978897356493767, 0.004676183784223950, 0.004402947947420276, 0.004155322065036335, 0.003930067232554567, 0.003724452812806255, 0.003536162241030836, 0.003363218787166214, 0.003203926550702888, 0.003056823192245135, 0.002920641788158231, 0.002794279835260507, 0.002676773902550357, 0.002567278775258057, 0.002465050197000034, 0.002369430512324879, 0.002279836661404447, 0.002195750093182894}
Keywords
sin, cos, Sinh, ArcSinh, ArcCos, elementary function, inverse function, Inverse trigonometric function, complex map, C++